突然ですが、2つ質問です!
1「たし算」と聞いて、思い浮かべるイメージは次のうちどちらが近いですか?
A
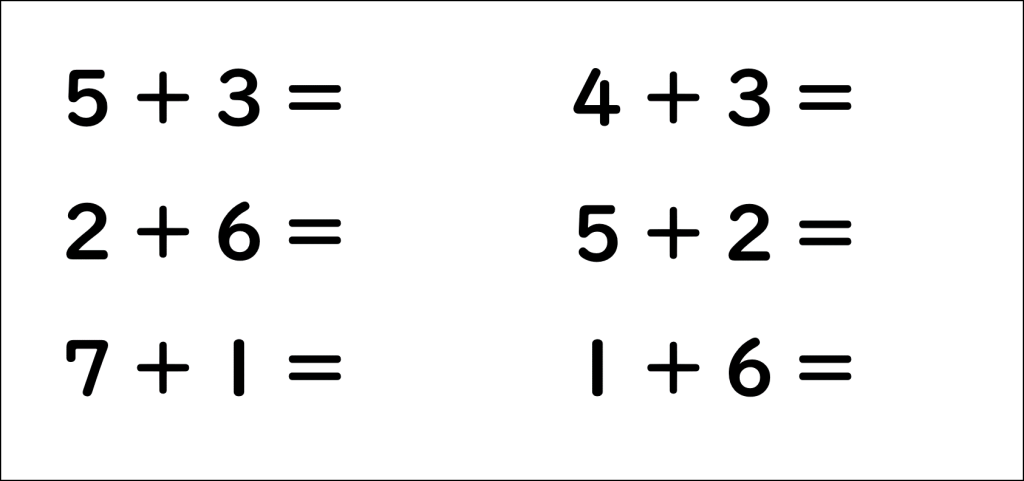
B

2 あなたがはじめて「たし算」をやったのはいつですか?
A 小学校に上がる前
B 小学校1年生のとき
C 小学校2年生以降
もし、両方ともAだったあなたは、知らない間に落とし穴にハマっているかも……

なーんて。

すみません!(笑)いきなり脅かしてしまいましたが、今回もどうぞよろしくお付き合いください。
パパ・ママに向けて、子どもの算数センスを磨く声かけ・働きかけのコツをお伝えしていきたいシリーズ第4弾!
今回は計算についてです!
パパママ、育児お疲れ様です!
改めましてこんにちは!math channelマガジン編集部のずーです。
今回扱う単元は、「四則演算」
たし算・ひき算・かけ算・わり算の4つの計算のことですね。
算数といえば、こちらを避けては通れません。
ほぼすべての算数・数学に関連してくる基本の術とも言えます。
この四則演算、1つ1つでも十分ボリューミーな気がするのに
なぜ4つまとめて記事に?と思ったそこのあなた! するどいです(笑)
今回は4つの計算それぞれの声掛けのコツというよりも、計算との向き合いかたとでもいいましょうか。
全体的なことについて話させてください。
はじめに習う四則演算といえば、「たし算」
冒頭に2つ質問しましたが、みなさんの答えは何でしたか?
これは私の肌感覚なので違っていても怒らないでいて欲しいんですが……
両方ともAの方が多いんじゃないかと思います。
まずはじめの質問「どちらがたし算のイメージ?」ですが、
「+」に慣れ親しんだ私たちは、この記号をみれば否応なしに「たし算」だと思うわけで、逆に「たし算」と言われたら「+」の記号やAの画像みたいな式を想い浮かべますよね。私もそうです。
それから2つ目の質問「いつたし算できた?」については、よく「小学校に上がる前にたし算くらいできるようになった方がいいですか?」と相談されることがあって、みなさん「1年生になる前の子でもたし算はできるし、なんなら自分もやっていた」という印象があるのかな?と思った次第です。
さて。
この、「小学校に上がる前に、たし算ができるようになった方がいいのか」
というパパママの疑問ですが……
こちらが今回のお話ししたいことに深く関わってきます。
先に、私の思う答えをお伝えしましょう。
それは……
もしこの疑問においての「たし算」のイメージがA
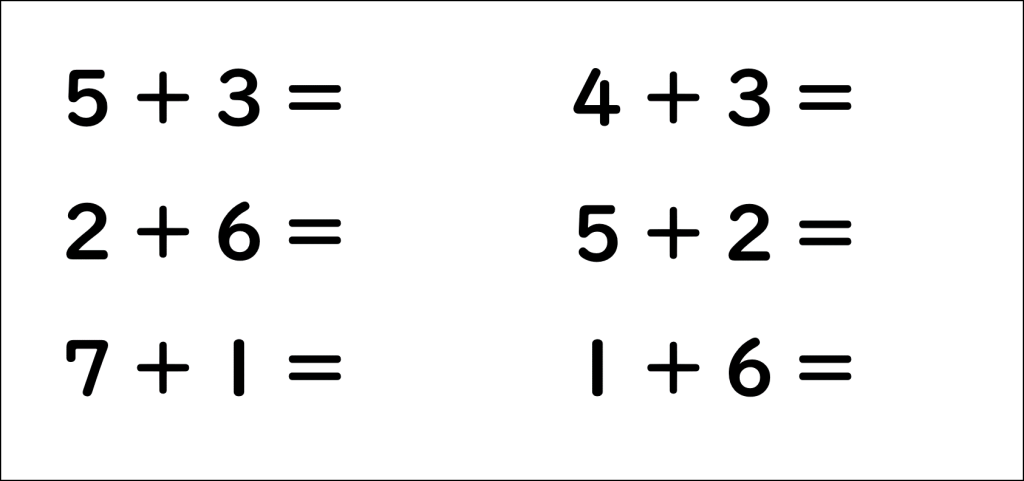
なんだとしたらNOで、
イメージがB

だとしたらYESです。
……
……
……どっちやねーん。
●●はNG??
くわしく話していきますね。
イメージがBなら就学前にできるようになった方がいい。とお伝えしましたが、
正しくは、たし算をできるようになった方がいいというよりは、たし算の場面についてたくさん考える、その際の思考回路を丈夫にすることが重要だと思っています。
「あわせたらいくつになるだろう?」
「ふえたらいくつになるだろう?」
という問いを日常的に考える機会は、どしどし作りましょう!
けれども、イメージAみたいな計算ドリルをするのはおススメしません。
というより、ドリルはやったらいけません。ぐらい言いたいです。
なんか、気持ちはわかるというか……わかる!そう、わかるんですよ。
もし就学前の年中さん・年長さんで、たし算ドリルをやってる子がいたら、「すごーい、〇〇ちゃんもうたし算できるんだ?」なんて、言ったり言われたりするでしょう??
たぶん、そんなことを園の友達から聞くから、「やっぱり就学前に……」という相談もくるんじゃないかと思います。
実際私も出会ったキッズに「ねえねえ、5+3わかるよ!8でしょ?」と言われたら、
「おお!『たす』って言葉もう知ってるんだね~!そうそう、8だよ!」
と返すことがあります。
実際5+3がわかることは素敵じゃないですか。
1つ新しい世界を知って、扱えるようになったことに賞賛を送らない理由はありません。
このこと自体に何も罪はないのです。
ただ……
同時に「この子の中で計算問題に正解することが正義になりすぎないといいなあ。」と思います。
計算そのものは目的じゃない
計算というのは、道具みたいなものです。
さきほど言った「あわせたらいくつになるだろう?」「ふえたらいくつになるだろう?」
という疑問を解決するための思考に「たし算」という名前をつけて、数を扱う際の記号「+」を用意したもので、これを正しく処理できるに越したことはないのですが、その先に解決したいことがなければ意味を持ちません。(※1)
カッターを上手に扱えることは素敵なことですが、その技術で何を作るのか?という話です。
そんなのは当たり前だと思う方もいるでしょうが、
実際には、計算問題を正解することには長けているけれども、その術を必要とするのはどんな場面であるかということに無頓着な子は結構います。
「あわせたらいくつなんだろう」という疑問に応えるのがたし算だという感覚が抜けたまま計算の練習をして、それに丸がつくことだけに関心を寄せてしまうと、一見「たし算がよくできている」のに実際はわかっていないという状態になってしまいます。
テストの点数も悪くはないんですよ。たし算の単元では、たし算をしとけば正解できるので。
ただ、その状態が続くと、いよいよ四則演算すべてを習い終わった小3あたりになって、文章題を読んで「これって7と4をたしたらいいんだよね?それともかけ算?」なんて言い出します。
私が「さあ、どうだろうね~」と答えずにいると、勝手に違ったんだと判断して「あ、やっぱりひき算か~」なんて言ったりもします。
作業よりも、考えること。
これでは、算数の楽しさからは遠のいてしまいます。
何算をすべきかを提示してもらって処理をするのは計算機でもできるわけで、
算数で考えたいのは、「どうやったら解決するのか」という部分です。
ダンボール工作で家を作っている
↓
この壁に窓を作りたい
↓
どうしようか
↓
カッターで繰り抜こう!
という判断を通して、作りたい形ができることに喜びは生まれるのであって、
カッターを使って切り抜く行為そのものはただの作業なんですよね(※2)
つまり四則演算では、
工作でいうところの窓を繰り抜きたい!にあたる、
あわせた数を求めたい!
面積の違いを知りたい!
同じものがいくつかあるぞ!
1人あたりの点数を知りたい!
という方針を見定める作業、そしてその方針に沿って適切な式を立てることが大事になってきます。
というわけで、
就学前に計算処理そのものに意識が向いてしまう計算ドリル(だけ)をするのはおススメしません。
ただ、誤解しないでくださいね。
そもそも「たし算」って言われたら、やっぱり「+」の記号が思い浮かぶじゃないですか。
だからたし算のイメージがBじゃなくてAでももちろんいいんです。
でも、Aのイメージのまま「たし算ができるようにさせたい!」→「ドリルをするのがよい?」と考えるのはちょっとストップ!という話でした。
小学校に上がる前にしたい四則演算の声かけ
では、計算ドリルではないとしたら、たし算や他の四則演算に慣れ親しむために一体何をしたらいいんでしょう?
それは、
「ふえたらいくつになるだろう?」
「等しくわけたらいくつずつになるだろう?」
という疑問について考えるべき場面に遭遇することです。
例えば、
 キッズ
キッズねえねえ、今日もどんぐりみつけたよ。
 パパママ
パパママほんとだ。
あ、ぼうしついてるのもみつけたんだねー!かわいい!
昨日の(8個)と一緒にしとく?
 キッズ
キッズうん!
 パパママ
パパママはい!(入れ物を渡す)
何個になった?
 キッズ
キッズえっと…1,2,3,4,5,6,7,8,9,10,11,12…12個!
 パパママ
パパママいっぱいみつけたね!
もともといくつか(8個)あったどんぐりが、今日の新入りによって数が(4)増えて12個になる。
たし算の場面ではありますが、このやりとりには「+」の記号も式もいりません。
おそらく、みなさんが本当にはじめてしたたし算はこんな感じのものだったのではないでしょうか。
(そしてこれなら就学前からしていた印象になりますよね。)
小学校に上がる前に、記号や式を使った計算を習う前に触れてほしいのは、こうした、
「8個から4個ふえて12個になった」
「20本を5人でわけたら1人4本になった」
という四則演算の場面を経験することです。
そんな場面どこにあるのー??
という方には!
どんぐり以外の具体例について、次回の後編でたくさんご紹介できたらと思います!!

お楽しみに♪
ちなみに……
この体験が十分にできていればドリルなどの計算の練習もいいと思うのですが、私は「+」の記号や式なんてものは学校で習えばいいと思います。早くから知ってたら授業中やることなくなっちゃうし。
親じゃなくて先生から聞いた方が、「先生は教えてくれる大人。親は居場所を作る大人」として役割分担がうまくいくし!
小学校の授業で習ったときに、「へ~! 今まで考えたことあった場面だけど、それたし算っていうのね。『+』って記号と数字で考えたことを式に表せるのね。便利じゃん。OK!これからはそれ使っていきましょ~」ってなるのが理想かな。と、思います。
それでは!
前編はこの辺で。

お読みいただきありがとうございました!!
【補足】
※1 計算は、解決したいものがなければ意味をなさない。
※2 カッターで切り抜くのはただの作業。
文脈上このように表現しましたが、実際には計算を何度と繰り返すうちに数の世界に魅了されたり、カッターでもっと細く上手に切りたい!と試行錯誤するうちに切り絵にはまるパターンなど、新たな意味を見出すことはありえるかと。それはそれで素敵なことですね!










