中学入試の算数指導歴30年 滝澤です。
2022年の中学受験が、2月上旬にほぼ終わりました。目標に向かって一生懸命戦ったすべての小学６年生のみなさん、お疲れ様でした。４月に素晴らしいスタートがきれますように。
さて、今年も多くの算数の良問に出会うことができました。今回はその中でも、有名中学の出題の中から面白い問題ベスト３を選んでみたいと思います。
面白い問題とは
私なりの「面白い」の判断基準ですが、
- 小４・小５でもチャレンジできる単元・難易度のもの
- 解法の知識などがなくても試行錯誤をくり返した末に答えを導き出せるもの
- 手間がかかりそうだけど，工夫によって簡単に解けるもの
などが挙げられます。
ではさっそく、第３位から参りましょう。第３位は２問あります。
第3位は２つ！
3位 その1 市川中 第1回 大問4
以下の会話文中のアからクにあてはまる数を答えなさい。ただし、答えが複数ある場合はすべて答えなさい。
X:「下の筆算が成り立つように、各アルファベットに0から9までの数を1つずつ入れることを考えよう」
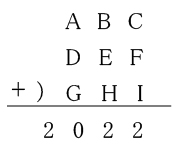
Y: 「それなら簡単だよ。AとDとGが6で、BとEとHが7で、CとFと1が
4ならば,674+674-674-2022 が成り立つよ。」
X:「そうだね。では、同じ数が使えなかったらどうだろう。各アルファベット
に入る数が異なるように0から9までの数を1つずつ入れられるかな。まず、 一の位のみに着目すると、C+F+1 として考えられる値は何があるだろう か。」
Y : 「アが考えられるね。」
X:「次に繰り上がりと十の位の数のみに着目してB+E+Hの値を考えてみよう。」
Y「イが考えられるね。同じようにして,A+D+Gの値はウが考えられる よ。」
X:「これだけだとまだ各位の和の候補が多くて決められないね。でも、各アルファベットには0から9までの中から異なる9つの数が入ることを考える と、各位の数の和の組合わせは1通りに絞られるんじゃないかな」
Y:「C+F+I＝エ、B+E+H＝オ、A+D-G＝カだね。ということは、0から9の中で使わない数はキなんだね。」
X :「では、Aが7のとき、残りのアルファベットに入る数の組合わせが何通りあるか求めてごらん。」
Y:「わかった。ク通りだね。」
3位 その2 渋谷教育渋谷中 第1回 大問1(5)
3桁の数ABC, DEF,GHIの3つを足したら2022となりました。
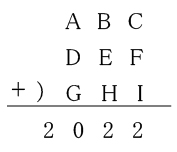
A～Iには、0～9までの10個の数字のうち、9個の異なる数字が1つずつ入ります。また、Cは6,Hは0です。A～Iで使わなかった数字をPとします。 ABCが考えられる数の中で一番大きい数になるとき、BとPはそれぞれいくつですか。
Takizawa’s check
これらの問題はどちらも、1月3日の記事の中で扱った問題とそっくりでした。
予想的中ということで，Twitterでも話題にしていただきました。
1月3日の記事とこの2問を見比べて、共通点や違いを楽しんで頂ければと思います。
パズルを入試問題にするために、いかに答えを出す過程を中学の先生方が重視しているかを感じることができます。そして大切なのは、やはり試行錯誤だということがわかりますね。
ちなみに、市川中の問題の解答は、
ア 12、22 イ 10、11、20、21 ウ 8、19 エ 12 オ 11 カ 19 キ 3 ク 144
渋谷教育渋谷中の問題の解答は B 7 P 3 となります。
また、2023年の予想問題はこちらの動画でも紹介中！
第2位 開成中 大問1(2)
次の計算の結果を9で割ったときの余りを求めなさい。
1234567 + 2345671 +3456712 + 4567123 + 5671234
Takizawa’s check
この問題は、がんばって全部たしてから、9でわるという計算をすれば小４生でもかんたんに解けるはずです。でももちろんこの問題はそのようにして解くよりもっと楽な解法はないか、考えることが大切な問題です。
まず、はじめの数である「1234567」を９で割った余りを考えましょう。そのまま割り算をする？いいえ、ここで思い出しておきたいことがあります。それは、「９で割りきれる数（９の倍数）の見分け方」です。
9の倍数の見分け方とは……
というものです。
知っていましたか？
もし知らない場合でも、9の段の答えには共通点があることに気づいていた人は多いのではないでしょうか。９、18、27、36、45、54、63、72、81、90。これらはすべて各位の数の和が9ですね。
そして、90の次に9で割りきれる数である99は各位の和は18です。いろいろな9で割りきれる数を書いてみて、各位の和を計算してみましょう。すべて9で割りきれるはずです。
さてそれでは、問題にもどりましょう。1235467の各位の和を計算して９で割ってみます。
1＋2＋3＋4＋5＋6＋7＝28、
28÷9＝3余り1
となります。ここでもし、「おしい！」と思えたら算数のセンスがかなりあります。
だって、何がおしいのかというと、「あと１小さければ9で割り切れたのに！」ということだからです。その通り。1234566ならば9で割り切れたのです。
ということは、1234567を9で割った余りは1ということになりますね。
ここで気づきます。実は、「各位の数の和を９で割った余りは、元の数を9で割った余りと同じ」なんですね。
よって、残りの2345671も3546712も4567123も5671234も各位の和は28ですから、９で割った余りは1。
よって、答えは、1＋1＋1＋1＋1＝5 となります。
なるほど！わかった！と思われた方。まだ気をぬいてはいけません。実は、
という疑問が残っています。これについては、自分で調べてみましょう。
数学のYouTuberとして有名な鈴木貫太郎さんが動画で、この問題を扱っておられます。
第1位 筑波大附属駒場中 大問２
縦と横にまっすぐな道が何本か通っている街があります。縦の道を1, 2, 3, …, 横の道をアイ,ウ,…として,縦の道と横の道が交わる場所をすべて「交差点」 と呼びます。たとえば、1の道とアの道が交わる場所は、交差点1-アと表します。
このような街で、交差点に警察官を配置することを考えます。警察官は,道を通 って他の交差点にかけつけます。道でつながっている隣り合う2つの交差点間の道 のりは、すべて1kmです。
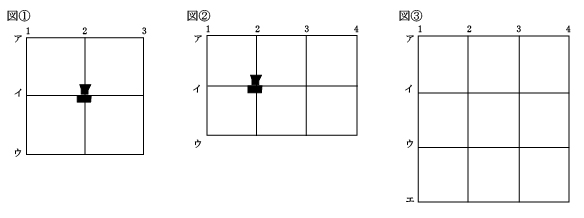
たとえば、図1のような、縦に3本,横に3本の道が通っている9個の交差点が ある街で、交差点 2-イに警察官を1人配置すると、街のすべての交差点に,警察官 が2km以内の移動距離でかけつけることができます。次の問いにこたえなさい。
(1) 図2のような、縦に4本,横に3本の道が通っている12個の交差点がある街に、2人の警察官を配置します。交差点2-イに1人目の警察官を配置しました。2人目の警察官をどこかに配置して、街のすべての交差点に、いずれかの警察官が2km以内の移動距離でかけつけられるようにします。2人目の 警察官を配置する交差点として考えられる場所は何か所ありますか。
(2) 図3のような、縦に4本,横に4本の道が通っている12個の交差点がある街に、何人かの警察官を配置します。街のすべての交差点に,いずれかの警置すればよいですか。考えられる最も少ない人数を答えなさい。
(3) 縦に15本,横に15本の道が通っている,225個の交差点がある街に,4人の警察官を配置します。このとき、街のすべての交差点に、いずれかの警察官が（ ） km以内の移動距離でかけつけられるように配置することができ ます。（ ）にあてはまる整数のうち、考えられる最も小さいものを答えなさい。
Takizawa’s check
問題文が長いですが、要するに、街のすべての交差点をできるだけ少ない人数の警察官でカバーする問題です。警察官はそれぞれ移動距離に制限があるために、どこまで移動できるかを考えなければなりません。
(1)と(2)では、警察官の移動距離が2kmですから、いったいどの範囲の交差点をカバーできるのかを試してみましょう。方眼紙やマス目ノートなどを使って図を描いてみるとよいと思います。例えば、6km×6kmの街であるとすると、1人の警察官のカバーできる範囲は下の図のような形になりますね。
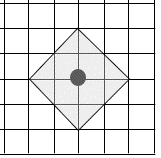
このように道と対角線が重なるような正方形の範囲になることがわかります。この正方形の範囲を様々にずらして考えてみると解きやすくなりますね。
(1)の問題であれば、1人めの警察官がカバーできない交差点は、4－ア、4－ウだけになりますから、2人目を配置する交差点は、4－ア、3―イ、3－ウ、4－ウの4ヶ所になります。
(2)はやはり2km以内の移動距離なので、1人目を「2－ア」に配置する。すると、図の範囲（境界線を含みます）の交差点にかけつけることができます。よって、2人目、3人目を「3－エ」「4－ウ」などに配置すればよいので3人でカバーすることができます。
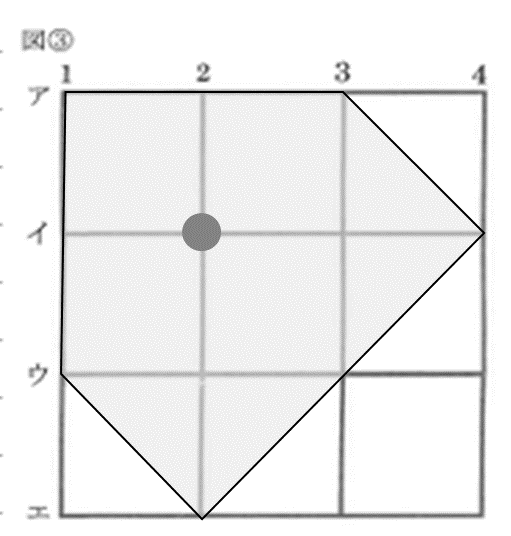
(3)は14マス×14マスの大きな正方形を方眼紙やマス目ノートに描いて考えてみましょう。(1)や(2)と違い、警察官がカバーできる範囲を考える問題ですから、いろいろな大きさの正方形を描いてみて、できるだけ少ない人数でカバーできるかを考えてみると楽しいと思います。
いかがだったでしようか。まだまだこれ以外にも楽しめる問題が多くの中学で出題されています。
気になる方は、「2022 中学受験 算数 問題」などで検索するか、または四谷大塚さんの過去問データベースに登録して気になる中学校の入試問題をのぞいてみるのもおススメです。
他の中学受験の問題にも取り組んでみよう！
中学受験算数の取り組み方は連載で紹介中！
（文責：滝澤 幹）
