一筆書きは非常にポピュラーなパズルです。皆さんも一度はやったことがあるでしょう。
一筆書きとは、
- 鉛筆やペンを紙から一度も離さない
- 同じ線をなぞららない
- 点で交差するのはOK
という条件のもとで図形を描くパズルです。言葉で説明すると大袈裟な感じがしますね。
新鮮味を感じてもらえるように、その背景の理論も少し感じられるようにしたいと思います。是非最後までお読みください。
まずは、問題にチャレンジ
まずは、問題です。次の図形を一筆書きしてみてください
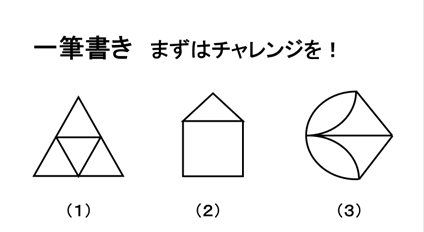
全部できましたか？
実は（１）と（２）は一筆書きできますが、（３）はできないのです。（３）にたくさんの時間を使った方、ごめんなさい。
では、どんな図形が一筆書きでき、どんな図形が出来ないのか、これからお話しします。
図形の分類と判定方法
図形は、一筆書きできる図形（上の問題では（１）と（２））とできない図形（３）の２つに分かれれるとお話ししましたが、（１）と（２）では違いがあることに気が付きましたか？
そうです、（１）は書き始めた点に戻って一筆書きが完成しますが、（２）は書き始めた点と終わりの点が違います。
つまり、一筆書きできる図形には、始点と終点が一致するものと始点と終点が異なるものがあります。まとめると次のようになります。
- 図形パターン１： 一筆書きできる、始点と終点が一致する
- 図形パターン２： 一筆書きできる、始点と終点が一致しない
- 図形パターン３： 一筆書きできない
この３パターンの判定方法を説明します。まずは言葉の定義です。
次数、偶点、奇点の３つを覚えてくださいね。
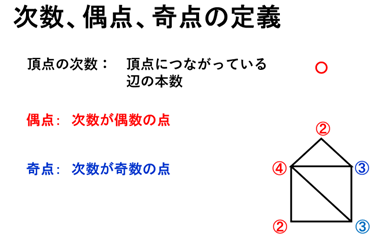
- 頂点の次数：頂点につながっている編の本数
- 偶点：次数が偶数の点
- 奇点：次数が奇数の点
この言葉を用いると、先ほど述べた３つのパターンは以下のようにして区別できます。
図形パターン１：一筆書きできる、始点と終点が一致する
すべて偶点から構成されている図形は、一筆書きができて、かつ始点と終点が一致します。
図形パターン２：一筆書きできる、始点と終点が一致しない
奇点が２個で、残りはすべて偶点から構成されている図形では、図形パターン2に属する図形です。
図形パターン３：一筆書きできない
奇点が３個以上ある図形は、一筆書きできない図形です。
最初の画像を改めて見てみると
つまり、一筆書きができるかできないかを判別する方法は、「奇点が３個以上あるかどうか」になります。
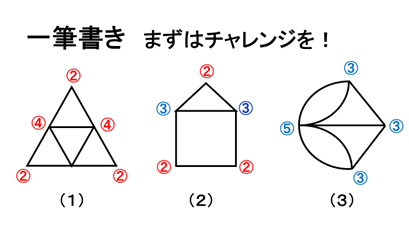
実際に最初にお出しした問題の図形に次数を付けたものをご覧下さい。下のようになっていますね。
雑巾は、一筆書きできる？できない？
最近、知り合いの方から、「雑巾に下図左側のような縫い目を付けたい。ミシンで一筆書きできないかな」と尋ねられました。ミシンで縫うときは、一筆書きの形で縫えると便利なのだそうです。
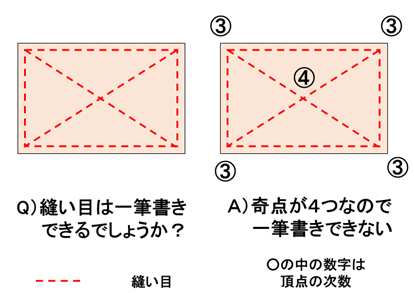
できるでしょうか？ 皆さんはもうお分かりですね。「できません」です。
判定方法を明らかにした250年以上前の天才数学者とは
図形が一筆書きできるかできないかは、250年以上前に天才数学者レオンハルト・オイラーによって明らかにされています。
つかみどころのない図形全体の性質を、構成する頂点の性質に局所化できると考えたことにオイラーの天才ぶりが現れていると思いませんか。
なお、この判定方法にまつわる話は「ケーニヒスベルグの橋の問題」として非常に有名です。本やネットで調べてみてください。判定方法のキーポイントとなるのは、図に示した偶点と奇点の性質です。
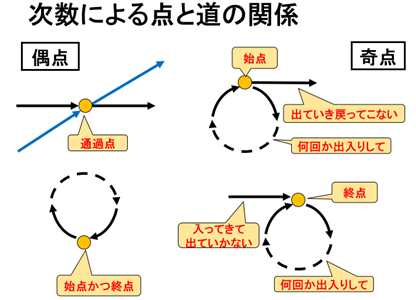
パターン1の図形の必勝法を紹介
さて、実際に書いてみると、複雑な図形では、一回でちゃんと書けないこともあり得ます。
パターン１の場合に、必ず書ける秘訣をご紹介します。
それは、始点（＝終点）を決め、そこから次々に辺をたどる際に、たどる辺の候補が複数ある場合は、その辺を除くと図形が２つに分かれてしまう辺（グラグ理論の用語では“橋”といいます）は、たどらないようにする、というものです。
この方法はグラフ理論の分野で「フラーリのアルゴリズム」と呼ばれています。
一筆書き、実は生活にも深いかかわりがある!?
一筆書きはパズルとしても面白いものであるだけでなく、私たちの生活にも、深い関わりがあります。
たとえば、除雪車や道路清掃車の巡回経路の決め方です。
一度の作業では同じ辺を1回しか通らない方が効率的で、道路を辺と考えると、このような経路はまさに一筆書きをすることと同じですね。
似たような問題に、各頂点をすべて１回ずつ通る辺を求める問題があります。
これは、巡回バスやごみ収集車の巡回経路の決め方に対応します。実は、このルート決めは一筆書きの問題に比べると格段に難しい問題です。
このような問題を数学的に研究する分野が「グラフ理論」です。実用性が非常に高い分野ですので、皆さんもこの分野に興味を持って下さると幸いです。
（文責：三浦章）
