ずーさん
ずーさんずーさんの『だったら算数ナゾトキ!』のページへようこそ!
この記事は、
小学生のみんなに楽しく算数にふれてほしい算数ナゾトキ★クリエイターのずーさんが、
①何かよい自学(自主学習)の算数ネタってないかな??
②もうちょっとゲームっぽい算数の問題ないの??
③ちょっとだけ、かるーく、予習(よしゅう)できたらいいな!
の声にお応えして、
 ずーさん
ずーさんだったらコレ!算数ナゾトキ!
を、出題(しゅつだい)&解説(かいせつ)しちゃいましょう!
そして、なんと!今お読みいただいているパパママ、もしくは小学生のみんなとナゾトキを作成しちゃいましょう!というものです♪

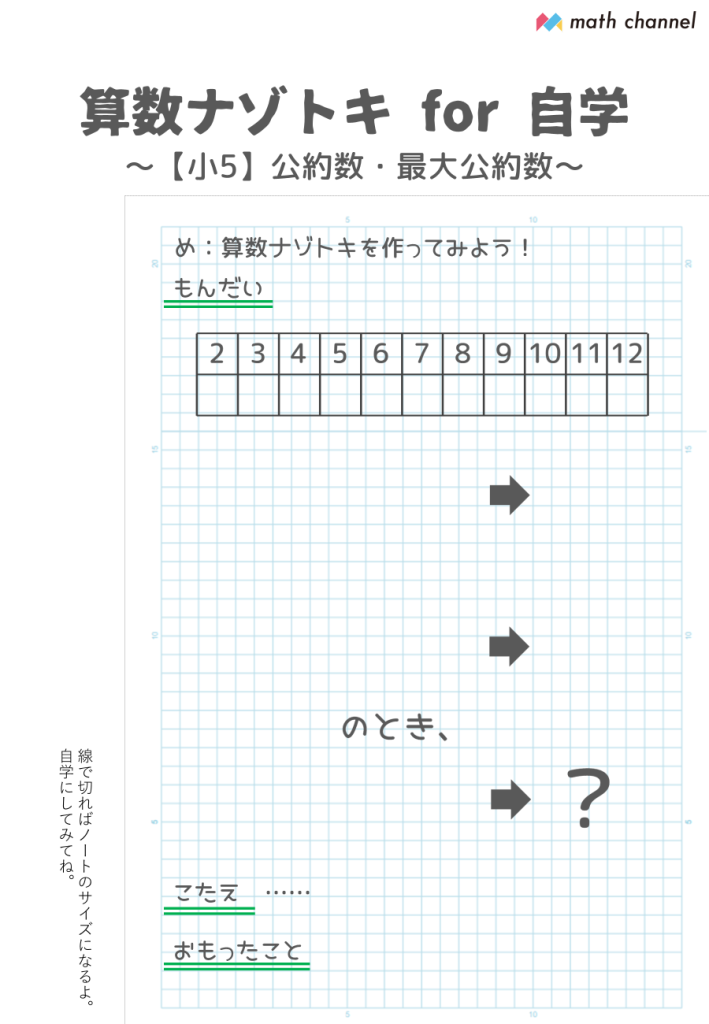
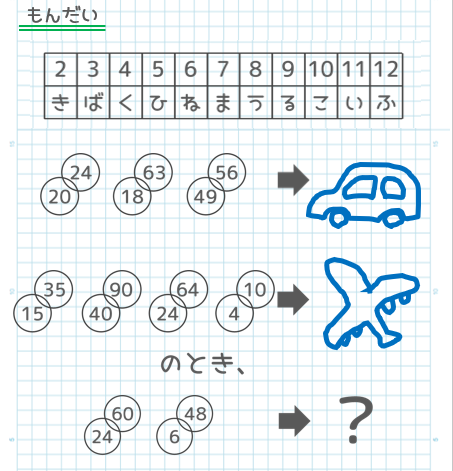
さっそく問題!
今回はとっとと出題しちゃいましょう!
関係する単元は小5で習うものですが、問題自体はかけ算・わり算の感覚(かんかく)があれば解けると思うので、小5より下の学年のお子さんもどうぞ挑戦(ちょうせん)してみてください!
(下にヒントをおいていきますので、見たくない方はスクロースせずに画像(がぞう)だけ表示がおすすめ)
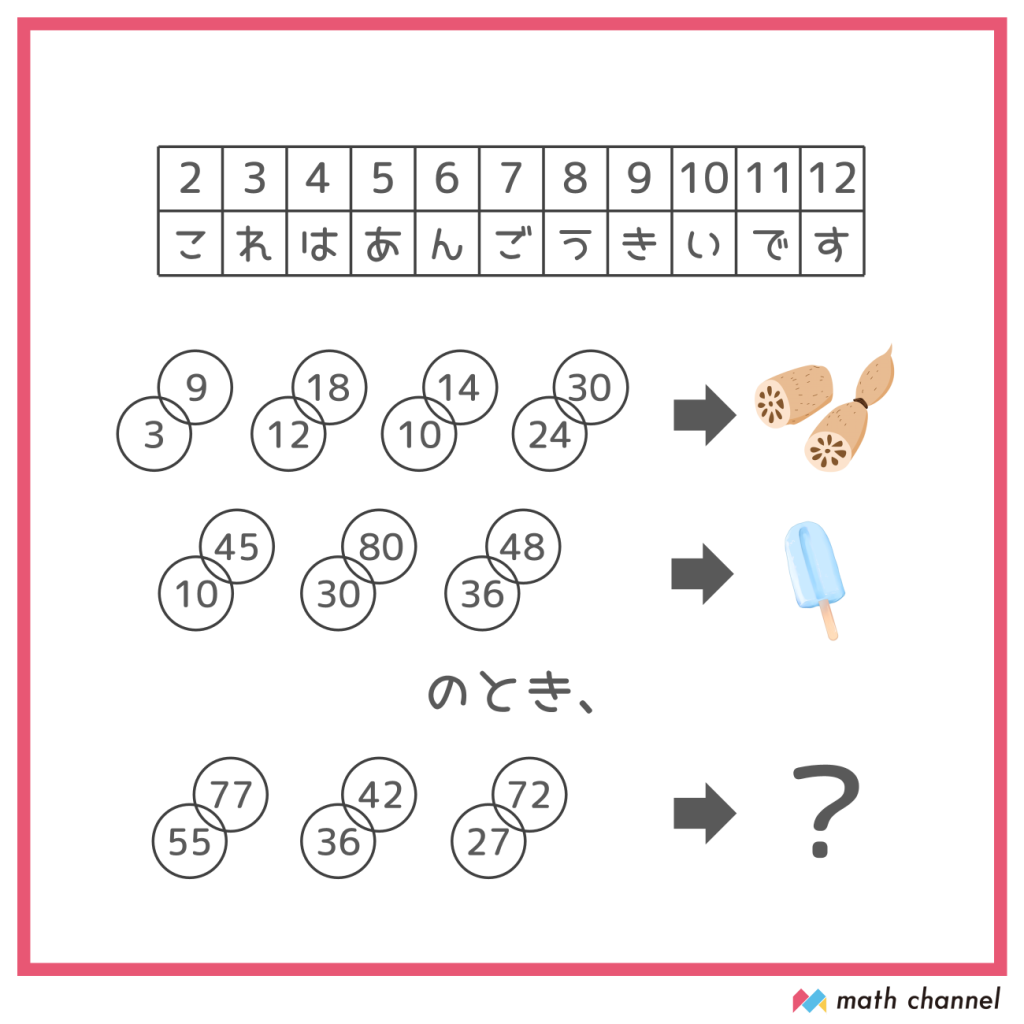
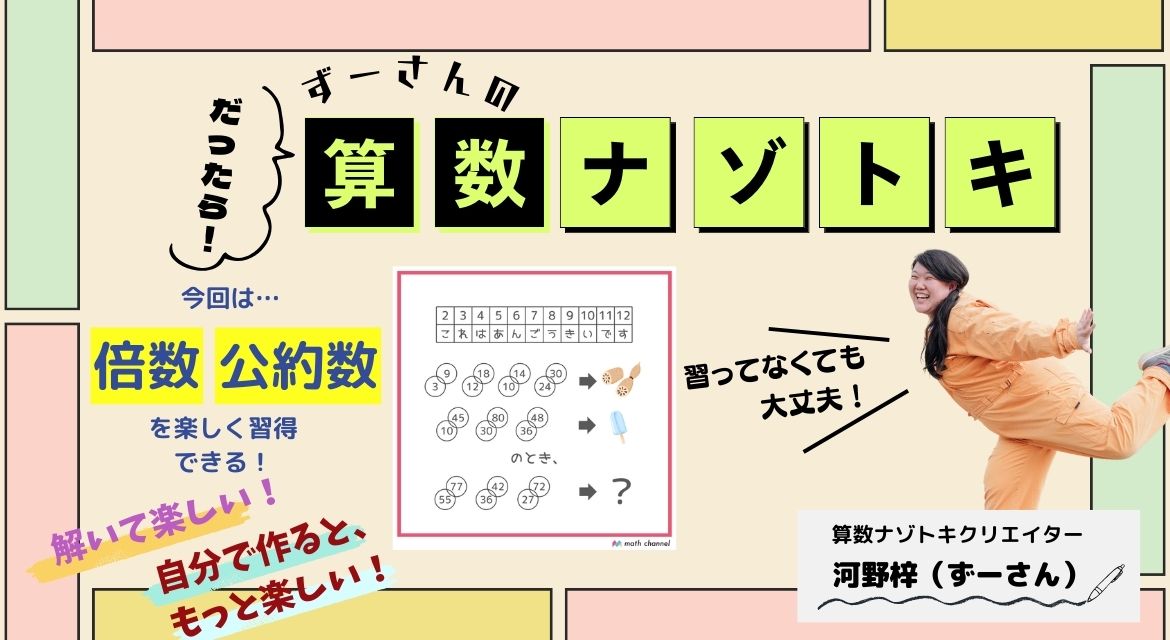
↓この下にヒントがあります↓
ヒント1
イラスト2つは「れんこん」と「アイスキャンディー」ですね。
左の円と数字でどうして右の言葉になるのか考えてみましょう!
↓次のヒント↓
ヒント2
「れんこん」に注目すると、「れ」も「ん」も「こ」も上の表にその文字がありますね。
となると、2つ目のイラストは「アイス」と解釈(かいしゃく)した方がよさそうです!
↓次のヒント↓
ヒント3
答えは、何文字になるでしょう?
↓次のヒント↓
ヒント4
どうやら、2つの円とその中の数字で、1つの文字を表していそうですよね!
ということは…?
↓次のヒント↓
ヒント5
3と9→「れ」
12と18→「ん」
10と14→「こ」
24と30→「ん」
10と45→「あ」
30と80→「い」
36と48→「す」
となるようです。
↓次のヒント↓
ヒント6
ひらがなは表と一致しているので、おそらく表の数と対応(たいおう)しています。
3と9→3で「れ」
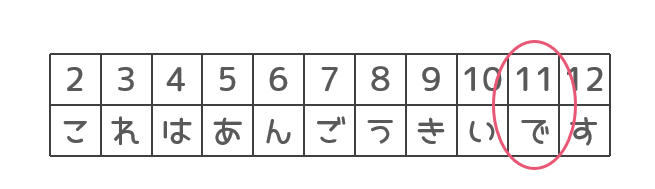
12と18→6で「ん」
10と14→2で「こ」
24と30→6で「ん」
10と45→5で「あ」
30と80→10で「い」
36と48→12で「す」
ということでしょう!
解説
今回は小3以上の方に解いていただいた想定(そうてい)で解説します。
2つの円に囲まれた2つの数から新しく1つの数をみちびくことができれば、あとは表に対応するひらがなを読むだけでよいことがわかりましたか?
では、2つの数からどのように新しい数をみちびいたらよいのでしょう?
注目したいのは、「れんこん」に2回登場する、「ん」の文字です。対応する数字は「6」。
同じ数字になるのだから、「12」と「18」、「24」と「30」には共通(きょうつう)することがあるはずです。
ピンときましたか?
どれも、6のだんの答えですよね!
実は、他の数字もながめてみると……
3と9→3×1と3×3→どちらも「3のだん」の答え→「3」
10と14→2×5と2×7→どちらも「2のだん」の答え→「2」
10と45→5×2と5×9→どちらも「5のだん」の答え→「5」
となっていたのです!
のこりの2つは九九ではありませんが、
30と80→10×3と10×8→「10」
36と48→12×3と12×4→「12」
ということで、
2つの数をかけ算で表したときに共通する数をみちびけばよいことがわかります。
この、2つの数に共通してかけられている数のことを公約数(こうやくすう)といいます。
「3」は「3」と「9」の公約数ですし、
「6」は「12」と「18」の公約数などと表現(ひょうげん)します。
「12」と「18」2つの数を両方(りょうほう)ともわりきることができる数が公約数。
という言い方もできますね。
であれば、あとは答えの3文字について1つ1つ解読(かいどく)していきましょう!
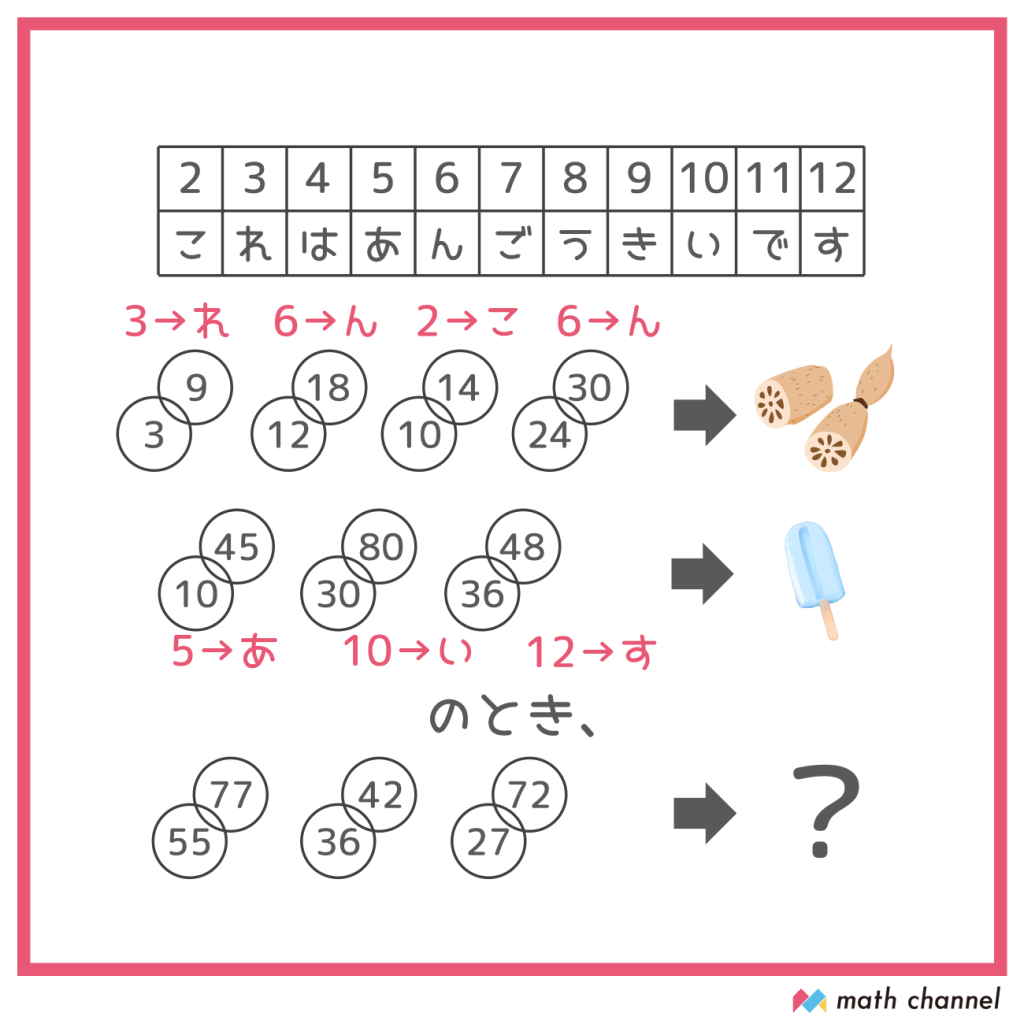
まずは、55と77ですね。
55=11×5、77=11×7なので、共通する数は「11」です。
表をみてみると、11に対応するひらがなは「で」!
次は、36と42です。
36=6×6、42=6×7なので、どちらも6のだんの答えなのですが……
1つとは限らない!
ここで、ちょっと疑問(ぎもん)に思った方はいませんか?
36と42は「6」も共通する数だけど、
36=3×12、42=3×14と考えれば「3」も共通する数ですよね。
また、
36=2×18、42=2×21と考えれば、「2」でも良いはずです。
はたして2文字目は「6」に対応するひらがななのか、
「3」に対応するひらがななのか、
はたまた「2」に対応するひらがななのか……どうしたらいいのでしょう?

実は、これには決め手があって、
どれも、考えられる共通な数のうち最大のものになっていました!
(よかったら、36と48などで確認(かくにん)してみてくださいね!)
というわけで、2文字目は「6」に対応する「ん」です!
そして最後は

27と72ですね。
これも、
27=3×9、72=3×24と考えれば共通する数は「3」
27=9×3、72=9×8と考えれば共通する数は「9」
となりますが、最大のものなので「9」に対応する「き」とわかります!
このように、公約数はいくつか考えられるときがあるのですが、
そのうち最大のものを最大公約数(さいだいこうやくすう)といいます!
解答と補足
というわけで、答えは「でんき」でした!
それから、もう1つ補足(ほそく)させてください。
例えばさきほど、27と72の公約数は「3」も「9」も考えられるといいましたが、
実はもう1つ公約数があるのです。何かわかりますか?
…
…
…
答えは「1」!
27=1×27、72=1×72なので、「1」も公約数なのです。
少し混乱(こんらん)しそうだったので、ここまでの説明でははぶいてきましたが、それぞれのペアの公約数には「1」もあることを知っておいてください。
つまり、27と72の公約数は「1、3、9」だし、
36と48の公約数は「1、2、3、4、6、12」ということです。
つくってみよう!
ナゾトキはいかがでしたか?
「簡単(かんたん)だった!」の方も、「やられた!」の方も、次は一緒に作ってみましょう!

 ずーさん
ずーさんこの単元が「ちょっと苦手(にがて)だな。」というお子さんには、どうぞパパママが作って類題(るいだい)にしてあげて下さい。
「自学としてやってみたい!」というお子さんは、ずーさんとレッツ・トライ!
作成にはこちらのPDFを印刷すると便利です。
手順1
まずは数字とひらがなの対応表を作りましょう!
どちらも何でもよいのですが、はじめは数字は小さい方がやりやすいと思うので、PDFのシートでは例題(れいだい)と同じにしてみました。
この表、「1」がありませんよね。最大公約数が「1」となる2つの数のペアはたくさんあるのですが、ちょっとこの謎で考えてみたいことから外れますし、表に1がないことが謎を解く時のヒントになると判断したので、1ははぶいています。
さて、問題はひらがなのほうです。本当に何でもいいので例題では「これは暗号(あんごう)キーです。」という文章をあてはめましたが、ココでは答えにしたい言葉から考えてみましょうか!
実際にノートにイラストがかけそうな、3文字か4文字のものを2つ思いうかべてください。
 ずーさん
ずーさんずーさんは「くるま」と「ひこうき」にしようかな!
そしてその文字を、表のマスにランダムに書いていきましょう。
こんな感じ!

また、謎の答えとなる言葉も考えていきます。答えはイラストにする必要がないので、例題の「電気」のようにカタチがないものでも大丈夫です。
 ずーさん
ずーさんのりものシリーズとして、答えは「ふね」でどうかな~!

え?3、4文字じゃなかったのかって?いいのいいの!(笑)
世の中、言われた通りにすることだけが正解とは限らないんですよ。
さらに、表の中にイラストと答えに使う文字を全部入れたら、あとは適当(てきとう)にうめておきます!

手順2
やじるしの右側(みぎがわ)にイラストをかきます。
イラストが苦手な方は、画像を用意したり文字で書いてもよいですよ。
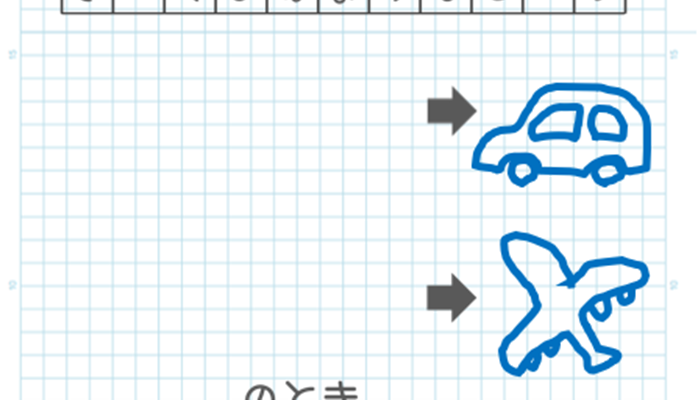
手順3
ひらがな1つ1つに対して、それに対応する数字を確認します。
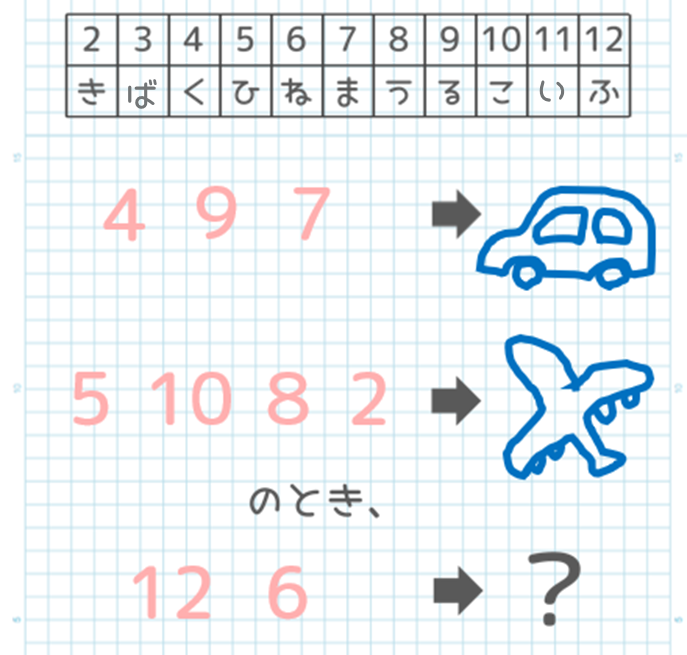
手順4
それぞれの数に対して、それが最大公約数となるような2つの数を考えます。
たとえば「4」だったら、まずは4のだんをいくつかあげてみましょう。
4×3=12、4×4=16、4×5=20、4×6=24
などですね。
こうやって考えるときにでてくる数
「12」「16」「20」「24」にも名前がついていて、(4の)倍数(ばいすう)といいます。
4に何か数をかけてできる数ですね。「4」も「4×1」なので「4の倍数」です。
九九の範囲(はんい)でなくてもいいので、4に100をかけてできる「400」だって「4の倍数」です。
そしてそのうちの2つを選べばOK!……なんですが、
もしかして、えらんだものによっては共通の数が最大にならない場合もあるので注意してください。
たとえば、「16」と「24」を選んだ場合、
16=8×2、24=8×3なので共通する数の最大(最大公約数)は4ではなく8になってしまうのです。
えらぶときのコツは、共通しない方の数に共通する数が1しかないようにすること。
ややこしいですね(笑)
さきほどの4つの数12、16、20、24でいけば、
4×3、4×4、4×5、4×6
なので、共通しない方の数は3、4、5、6です。
このうち、「4」と「6」はどちらも2がかけられているし
「3」と「6」はどちらも3がかけられているので適(てき)さないのですが、
「3」と「4」
「3」と「5」
「4」と「5」
「5」と「6」
の4ペアは共通する数(公約数)が「1」しかないのでOKなんです。
まあ、ここらへんはすぐにわからなくても大丈夫!
とにかく作ってみて、出題して、失敗すればだんだんわかってきます!
失敗は成功の母ですから恐れずにいきましょう。
むしろOKパターンとNGパターン両方に会うことで数と仲良くなれるのです!
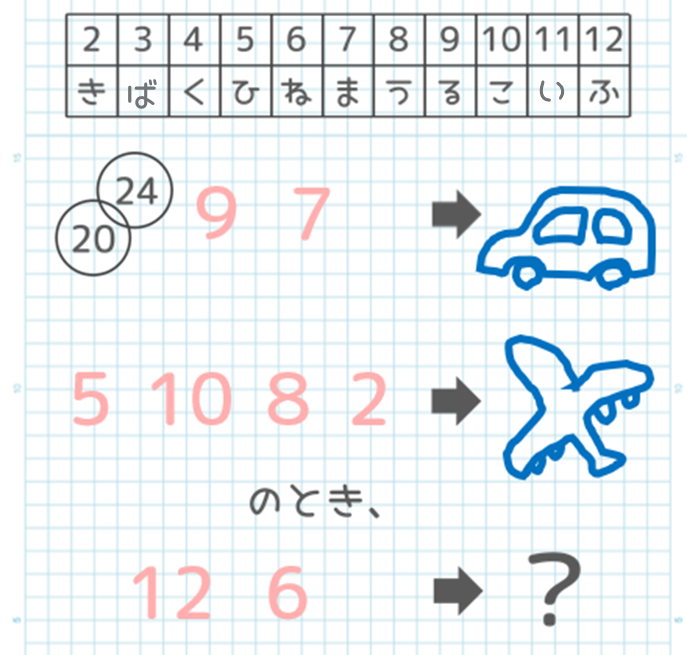
さあ、というわけで、4を表したいところには2つの円と「20」と「24」を書き入れてみました。
あとは同様に他の(文字に対応する)数についても、
ちょうどよい2つの数を考えて書いていけばできあがり!
せっかくだから、楽しくね!
いかがでしたか?
ナゾトキに挑戦することで、「2つの数の最大公約数を探す」
作問(さくもん)することで、「ある最大公約数をもつ2つの数を探す」ことができたかと思います!
今回の問題は、本当に答えを何にでもできるので、
ヒミツのお手紙などに使ってもおもしろいかもしれませんね!
そしてその過程(かてい)で、
どんどん「公倍数・公約数」への理解を深めていってくれたらうれしいです!
それでは、また次回の記事でお会いしましょう!
お読みいただき、

(文責:河野梓)
毎週出題しています!
ずーさんもせっせと作問中!
作った問題は私のXアカウントで公開していますので、よかったらのぞいてみてくださいね!
『算数ナゾトキ20』発売中☆
また、いろんな算数ナゾトキを20問集めた問題集も販売しています。