こんにちは、ずーさんです!
私自身、算数ナゾトキクリエイターとして活動しておりますが、みなさんは算数ナゾトキ、解いたことがありますか?いったい普通の謎解きと何が違うのでしょうか?
今回はそんな算数ナゾトキについて、徹底解説しちゃいます!
問題も出題!ぜひ解いてみてくださいね!
算数ナゾトキとは?
算数ナゾトキ(算数謎解き)とは、算数の知識や算数的な処理、発想を用いて解く謎解きです。
謎解きそのものの説明をWikipediaさんに聞くと、「パズル、推理、クイズ、脱出ゲームなどの形態を含むエンターテイメントの一種」とあります。これに算数の要素が加わったものが、算数ナゾトキなのです。
主に、
- 取り掛かりやすい
- 意欲的に取り組める
- じっくり考える機会になる
と言う3つの点から、算数の学習の選択肢においていただきたいコンテンツです。
といっても

という方のために!
実際の問題を紹介しながらその魅力を説明してみましょう!
どうぞ小学生に戻った気分で、全問クリアを目指して考えてみて下さい!
お子様と一緒に挑戦してみるのも良いかもしれません。

算数の知識を使うナゾトキ
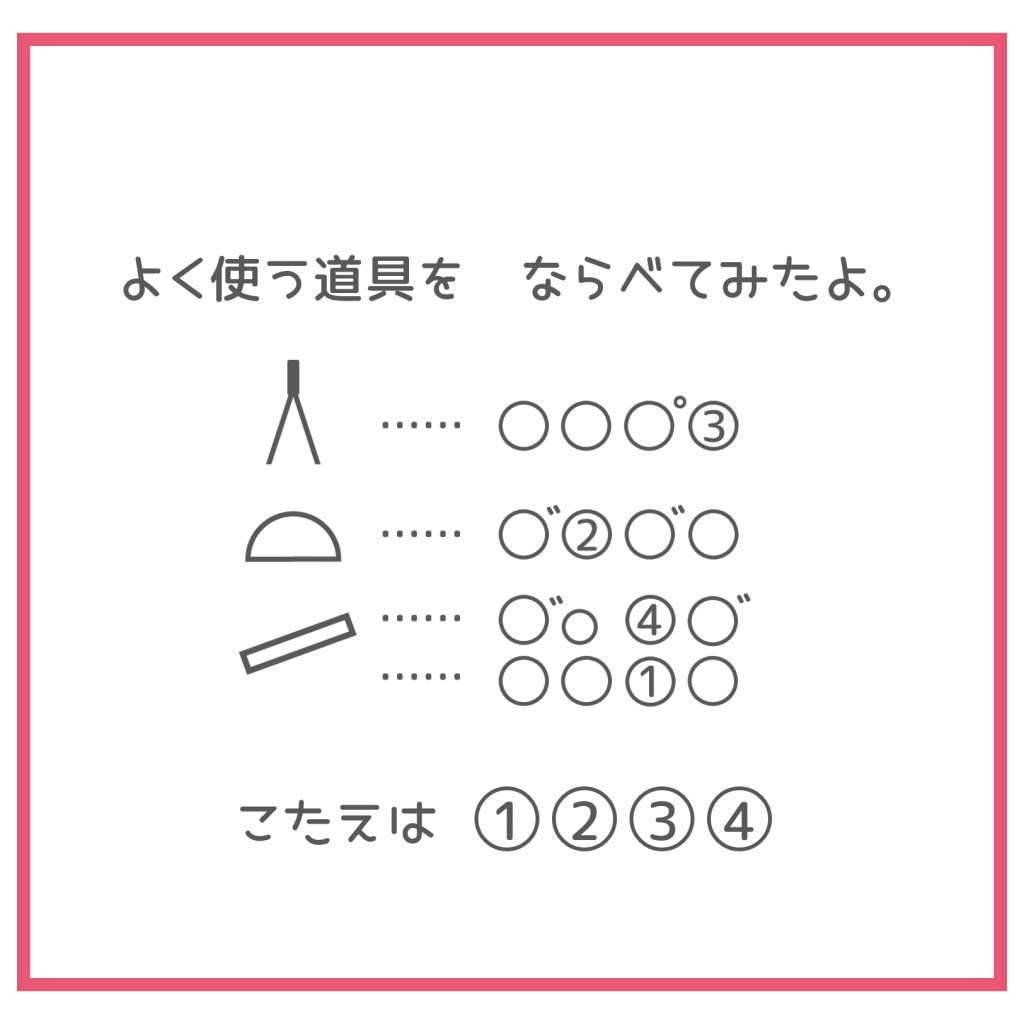
第1問は、ちょっとしたひらめきと算数で使う道具の知識が必要な謎解きです。
まずはノーヒントで解いてみてください!
ヒント1
算数で使う道具、何か思いつきますか?
理科ほど種類はありませんが、算数の道具は小学校では1人1人持つことが多く、身近にありますので、すぐにピンときたという方もいるかもしれませんね。
ヒント2
図は簡略化してあるので、逆になんだかわからないぞ??という方もいるかも。ざっくりと捉えて表現してあることを前提に考えてみてください。
1番上の道具は2つに分かれていて、実際は棒の先に何かくっついています。しかも左右それぞれ別のものがついてますよ。
真ん中にある道具は小4で出会うものです。角度を測るときに……おっと、言い過ぎたかもしれません(笑)
ヒント3
下の長方形がいちばん「??」ですよね。四角いものなどたくさんある気がしますが、形だけではなく文字が入るであろう〇の数や大きさにも注目してください。
小さい丸に入るのは「や」「ゆ」「よ」「つ」だけなので絞られますね。濁点「゛」のつく文字も限られます!
しかもこの四角、2通りに捉えることができるようです。
答え
もうわかりましたか?
上2つは「コンパス」と「ぶんどき(分度器)」です。
そして同じような測るもので、長細い四角いものと言えば……
そう、「ものさし」ですね。
また、まっすぐ線を引く道具と捉えれば「じょうぎ(定規)」になります。
それぞれの〇の中に、「コンパス」「ぶんどき」「じょうぎ」「ものさし」「じょうぎ」をあてはめると、①②③④に入るのは、「さ」「ん」「す」「う」
答えは「さんすう(算数)」でした!

算数ナゾトキの雰囲気、つかんでいただけましたか??
こちらはいわば知識問題。ものさしもコンパスも分度器も触ったことのある4年生以上なら解けたかな?といった問題です。
次はちょっとタイプの違う問題、いきますよ!!
算数的処理を用いるナゾトキ
こちらは基本的には小学校5年生以上の方に向けた謎解きになります。
まずはノーヒントでお出しします!
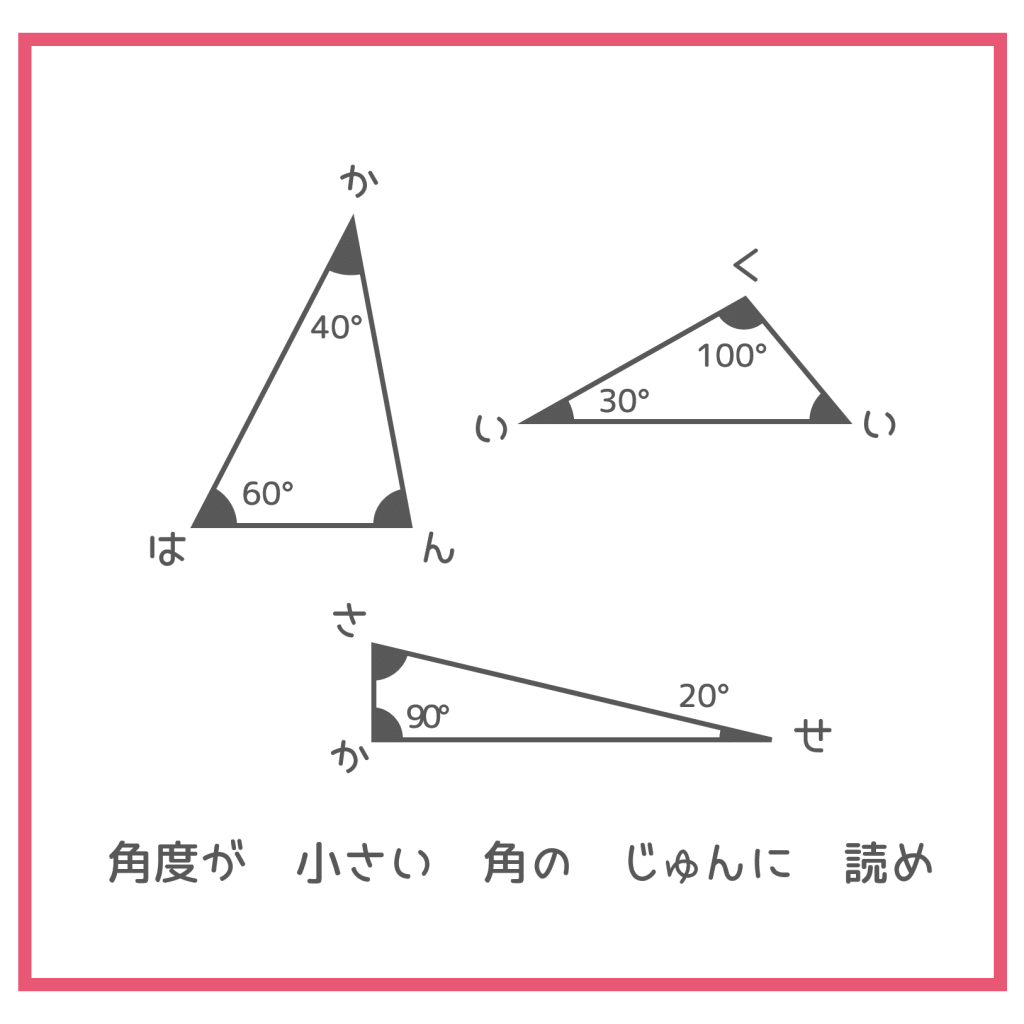
ヒント1
数字が書いていない角がありますね。でも、実はすべて角度がわかるのです。考えてみて下さい!
ヒント2
どれも三角形の角ですね。三角形の角と言えば、
3つの角(内角)の和は180度
という性質がありました。これが小5の学習内容です。
答え
数字が書かれていない角は、左上の「ん」が180°-(40° +60°)=80°、 右上の「い」が180° -(30° +100°)= 50°、下の「さ」が180°−(90° +20°)= 70°でした!
したがって、小さい順に並べてみると、
20° =せ
30° =い
40° =か
50° =い
60° =は
70 °=さ
80 °=ん
90 °=か
100°=く
正解は「さんかく(三角)」でした!
この問題で使う力は、教科書に出てくる
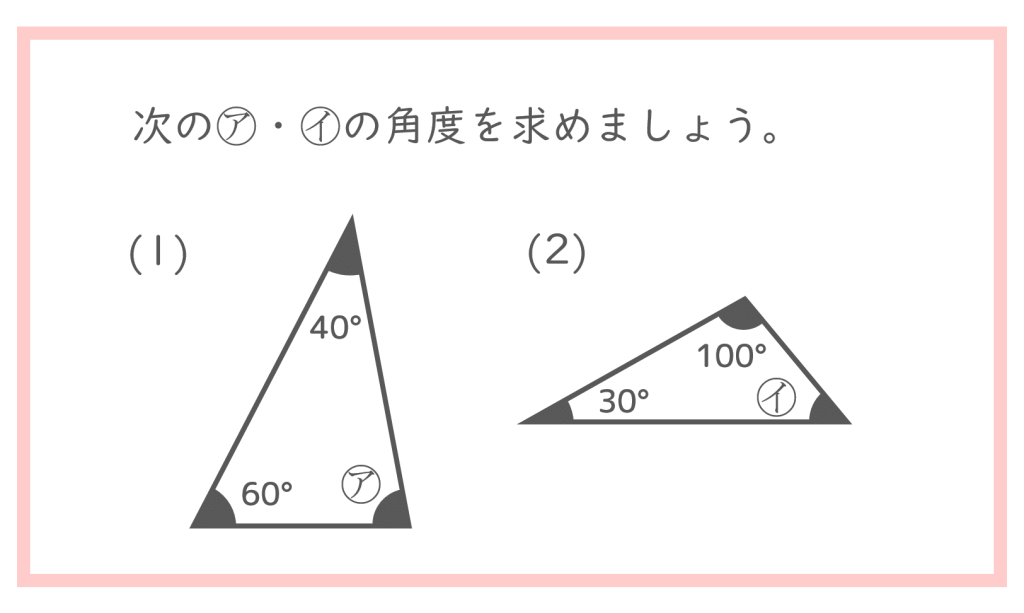
と、全く同じなのですが、ナゾトキでは答えが言葉になるので、「どんな単語が出てくるのだろう??」というワクワク感がプラスされる気がしませんか??
「日本でいちばん標高の高い山を答えなさい」というテストではなく、「日本一高い山は?」とクイズを出されると答えたくなってしまう感覚と似ています。
しかも、同時に3問練習できてしまうし、良さそうな言葉にならなければ、「何かがおかしい、計算ミスしたかな?」と、自力で修正することもできますよね!
算数的な感覚を用いるナゾトキ
実は、先程の問題には小5の学習内容が含まれていると書きましたが、小4生でも解くことができます。
「三角形の内角の和は180度」であることを知らなくても、小4で習う「角度」の意味さえ知っていれば、問題を捉えることができるからです。
デジタルの画面で見ている方が多いと思うので現実的ではありませんが、実際に角度を分度器で測ってみてもよいですし、何より見た目で小さいものから選べばよいのです。
「そんなのあり!?」と思うかもしれませんが、角度というものをしっかり理解しているからこそできる解き方だと思います。
算数の問題って、ややもすると型が決まってしまうので、その型の通りにするものだと勘違いするお子さんも少なくないのですが、本来解き方は自由なので、角の開き具合がどうであるかを見定めて解くのもOKなのです。
実際、算数を教えていると30°がどのくらいの角度なのか意識のない子が結構いるのですが、「計算した結果が15°だけれども、図のこの角度40°くらいありそうだからおかしいかも」という感覚や「この辺とこの辺が等しいといいんだけど、図のここ45°っぽいから、この三角形は二等辺三角形になるのかもな!」という見立ては、問題を解く上で大切な力ですし身に付けたいところです。(注:算数の問題に出てくる図は、あえて不正確に書かれていることもあります。)
ただ、例えばこの問題では「さ」の角度と「ん」の角度が見た目では判断しづらいので、そうなったときに、分度器で測ったり内角の和の関係から計算したりして、数の根拠を示せるとなおよいですね。
教科書には載らない算数の問題!?
こんな風に、「見た目の判断でいいから角度の小さい順にならべてみよう」なんて、算数の教科書にはなかなか出てこないけれども、やっていることはしっかり算数である問いを出題できるのも、算数ナゾトキの特徴です。
もう1問例を挙げてみましょうか。
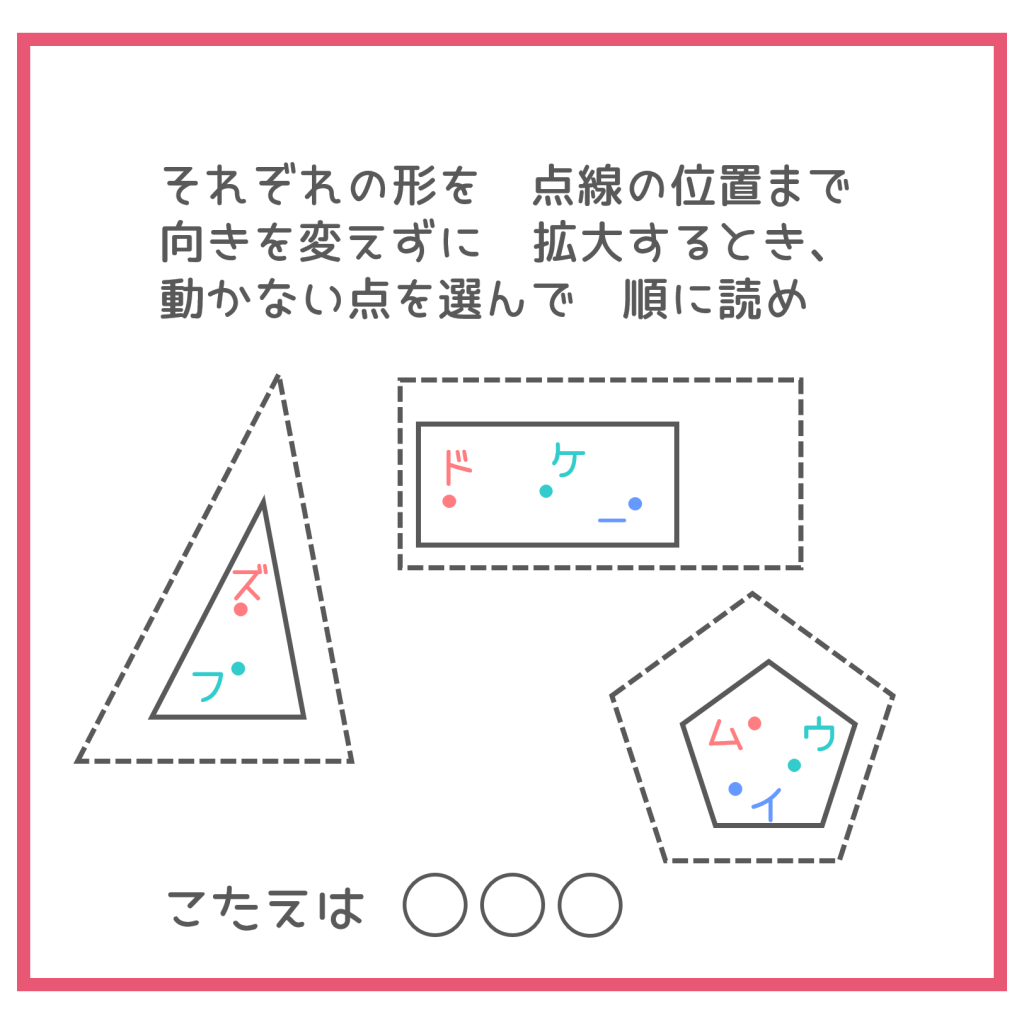
ヒント1
それぞれの形が、点線まで大きくなる様子をイメージしてみましょう。角(かど)はもちろん動いていきますが、動かないところがあるのです!
ヒント2
拡大する前と後で、対応する点同士を結んでみましょう。どこを中心にして拡大しているのか見えてきます。
答え
動いていない点はそれぞれ「フ」「ド」「ウ」なので、答えは「フドウ(不動)」です。
ちょっと小学生は使わなそうな言葉を答えにしてしまいましたが、解けましたか??
この拡大についての問題も、教科書であれば
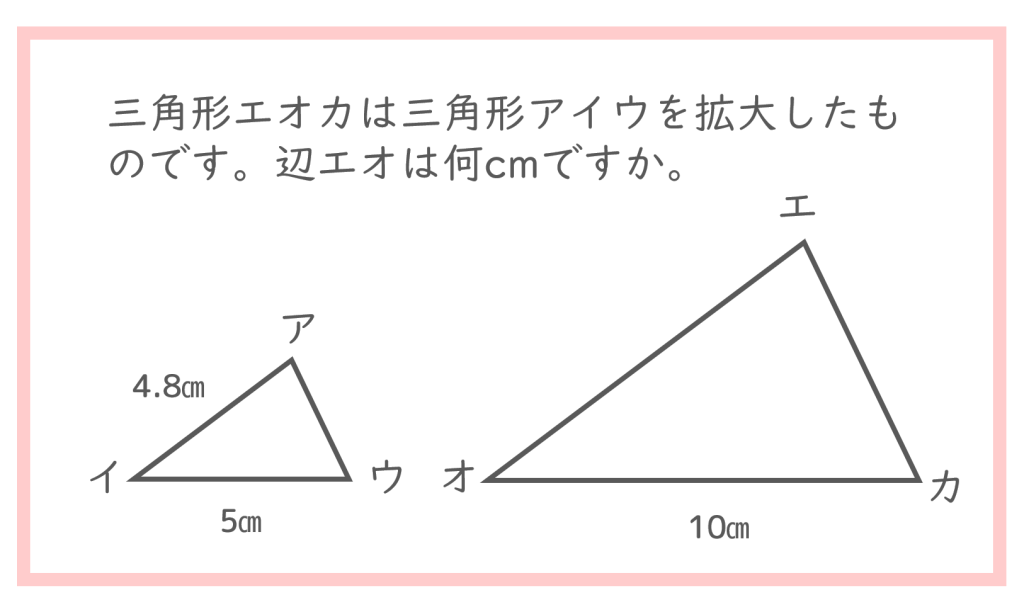
といったものが一般的なのですが、辺だけではなく、いろいろな長さに拡大の比があらわれるということを、拡大・縮小の学習から感じ取っているとできる問題になっています。
例えば文化祭などで大きな紙面に絵を描きたい時、まず小さい紙に書いてから大きな紙と角を合わせ、主要な点と角との距離が拡大すると何㎝になるかを求めていけばうまく写し取れるわけですが、そんな「使える算数」として学習内容が身についているかを問う一問にもなります。
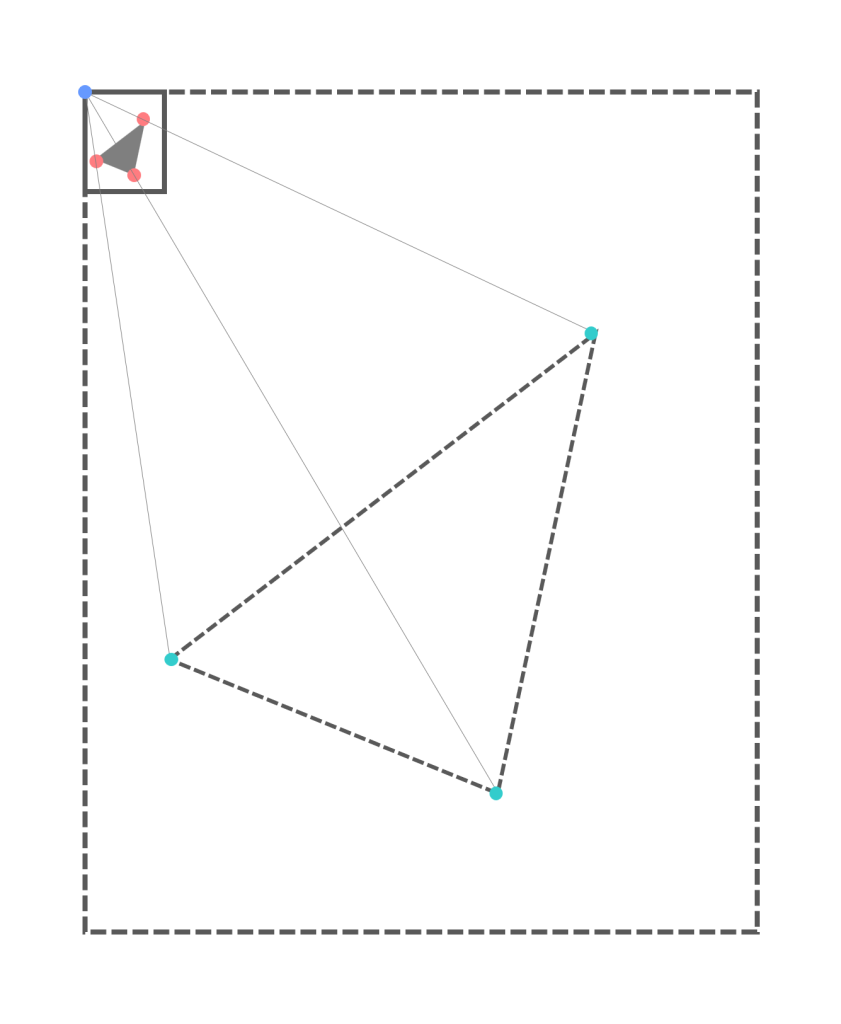
青ー赤の長さと、青ー緑の長さの比はどれも同じ!
また、こんな感覚があれば中学校で習う中点連結定理
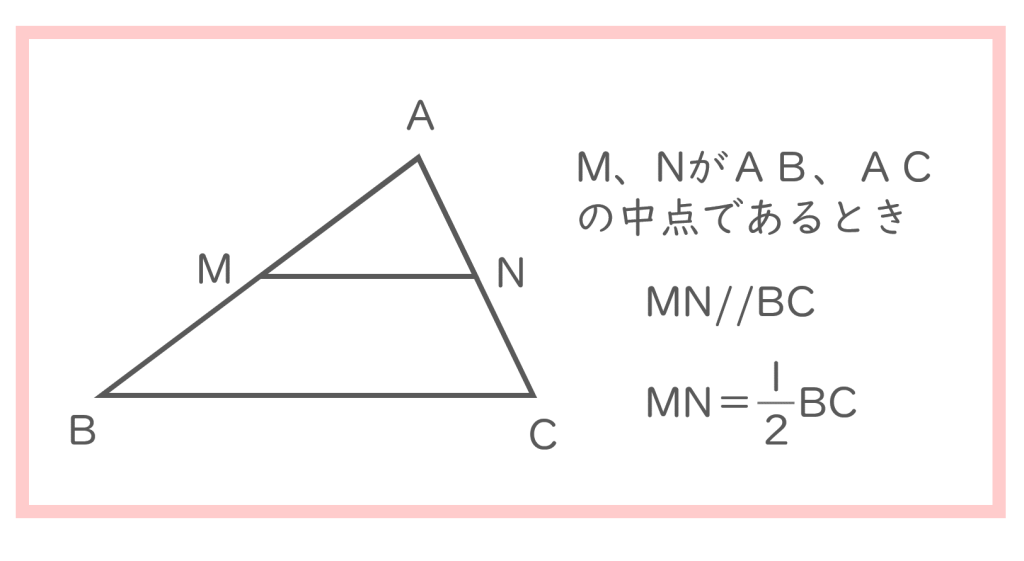
も、すぐに納得できるように思います。
そんなこんなで、教科書やテストでは出題されなさそうな算数ナゾトキならではの問題でした!
楽しい雰囲気で算数ナゾトキに挑戦してみよう!
実際に解いてみていかがだったでしょうか?
謎解きは、問いの意味、「何を聞かれているか」を探る問題も多く、それだけで考える力を使います。しかも見た目はクイズのような雰囲気で取り掛かりやすく、なんとなく答えを知りたくなってしまうのがその魅力です。

今回は1枚謎といわれる、1問だけで完結するものばかり紹介しましたが、これが組み合わさった、ある程度時間のかかる謎解きとなれば、さらに考えますし、解いた後の爽快感も格別です!!
機会があればそちらについてもまた紹介したいと思いますのでお楽しみに!
楽しく算数に触れられて、いつもの問題とは少し違う力も鍛えられる算数ナゾトキ、是非、親子で楽しんだり、お子様に勧めてみてくださいね!
ずーさんが算数ナゾトキを推す理由は?
こちらの記事も合わせてご覧ください!
お知らせ
算数ナゾトキをカード形式にまとめた『算数ナゾトキ20』ができました!
この記事で一緒に解いた角度の問題をはじめ、さまざまな種類20問を収録しています。

是非、お手にとって挑戦してみてください!
minneさんのこちらのページで取り扱っています!
https://minne.com/items/41324851
■ずーさんが書いた他の記事はこちら!