こんにちは。中学受験算数ナビゲーターの滝澤です。
前回は、図形問題の中でも紙を折る問題を紹介しました。
今回は、中学受験の算数では最頻出ともいうべき「相似と面積比の問題」です。
相似ってなに?
相似な図形とは、簡単に言えば「拡大コピー・縮小コピーの関係にある2つの図形」のことです。
この拡大・縮小率にあたる辺の長さの比のことを、相似比といいます。相似な2つの三角形を見つけて、相似比を考えることがこのような問題を解く王道です。
相似な三角形は、角度がそれぞれ同じという特徴があります。
拡大コピーをして角度が変わっちゃったら困りますよね。
王道の解法パターンの習得が大事
相似と面積比の問題は基本的な解法パターンがあって、それをしっかり練習していればある程度正解することができます。おおまかに言えば、
- 相似な2つの三角形の組を見つける。
- 2つの三角形の対応する辺の比を問題から読み取る。
- 対応する辺の比はそれぞれ等しいことを利用して、他の辺の比を計算する。
の3ステップが重要です。
王道の解法パターンをしっかり学習することは確かに大切です。ここを避けては通れませんが、問題によっては、このような解法の知識を知らなくても図の描き方を工夫することで答えを導き出すこともできます。
2022年の海城中学の入試問題を例にとってご紹介しましょう。
問題です。/海城中学(2022年、大問2)
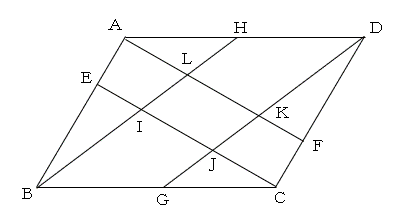
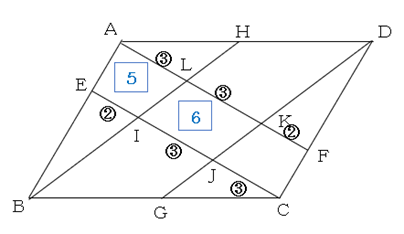
下の図のように,平行四辺形ABCDの辺ABを1:2に分ける点をE,辺CDを1:2に分ける点をFとし,辺BCと辺DAの真ん中の点をそれぞれG,Hとします。また,BHとCEが交わる点をI,CEとDGが交わる点をJ,DGとAFが交わる点をK,AFとBHが交わる点をLとします。次の問いに答えなさい。
(1) BI;IL:LHを最も簡単な整数の比で答えなさい。
(2) 平行四辺形ABCDと四角形IJKLの面積の比を最も簡単な整数の比で答えなさい。
(3) 平行四辺形ABCDと四角形AEILの最も簡単な整数の比で答えなさい。
まずは王道の解き方をしてみましょう。
王道の解き方とは、相似な三角形の組を探して相似比を考えるのでしたね。
(1) 三角形ABLと三角形EBIが相似で相似比が3:2ですから、BI:IL=2:1
また、三角形BCIと三角形GCJが相似で相似比が2:1ですから、BI:CJ=2:1
さらに、三角形ALHと三角形CJGは合同ですから、GJ=LHになります。
よって、BI;IL:LH=2:1:1です。
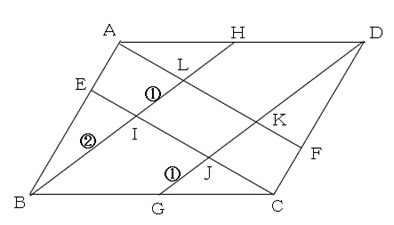
(2) まず、HとGはそれぞれ辺のまん中の点ですから、平行四辺形HBGDは平行四辺形ABCDの半分の面積ですね。
ここで、台形BGJIと平行四辺形IJKLと台形LKDHはすべて高さが同じですから、面積比は「上底+下底」の比になります。
(平行四辺形も台形の1種ですから、台形と同じ公式で面積を求めることができます)
(1)より、BI;IL:LH=2:1:1で、同様に、DK:JJ:=2:1:1になりますから、
台形BGJI:平行四辺形IJKL:台形LKDH=2+1:1+1:1+2=3:2:3
となり、平行四辺形IJKLは平行四辺形HBGDの4分の1になります。
平行四辺形HBGDは平行四辺形ABCDの半分の面積ですから、平行四辺形ABCDと四角形IJKLの面積の比は8:1ですね。
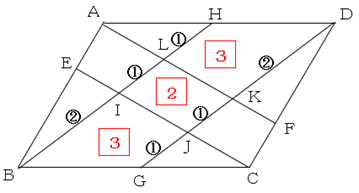
(3) AL:LK:KFについて、(1)と同様に比を求めます。すると3:3:2になります。
また,EI:IJ:JC=2:3:3になりますね。
四角形AEILと四角形IJKLは高さが等しいので,面積比は上底+下底の比となり、
3+2:3+3=5:6となります。(2)より平行四辺形ABCDと四角形IJKLの面積の比は8:1ですから、平行四辺形ABCDと四角形AEILの比は48:5になります。
とここまでが基本的な解き方となります。
基本的ですけれど簡単ではありませんよね。意外と手順も多いし、比がこんがらがりそうです。
もっと簡単な解き方はないのか?と考えよう。
問題が解けたら、うれしくてそれで終わりにしたいところですが、「別の解き方はないのかな?もっといい方法はないのかな?」と考える習慣がつくと、もう一段階上のレベルを目指せます。そしてそれが算数の面白さでもあると思うのです。
というわけでせっかくですから、裏技をお教えしましょう。
ここからが相似をつかわない裏ワザ
この問題の特徴は平行四辺形であることと、辺の比だけが定まっていることですね。
つまり、角度や辺の長さなどは自由に作図して考えても答えは出せるということです。
そこで1辺1cmの方眼紙にこの図をわかりやすく作図してみましょう。
AFとBHは直角に交わり、辺ADに対して45°になるように作図すると下のようになります。
四角形IJKLは対角線が3cmの正方形になりますね。
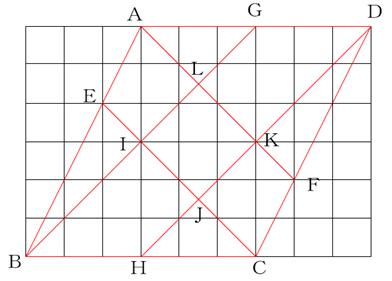
これを見ると、この問題は解きやすくなります。
(1)はBIが1辺1cmの正方形の対角線3個分、ILとLGはともに正方形の対角線1.5個分だから
長さの比は2:1:1
(2)は平行四辺形ABCDの面積は底辺が6cmで高さも6cmですから6×6=36で、四角形IJKLは正方形で、対角線×対角線÷2を使うと3×3÷2=4.5だから面積の比は8:1
(3)は四角形AEILの面積は三角形AEIが3×1÷2=1.5、三角形AILは正方形AIKGの4分の1ですから3×3÷4=2.25なので、合計3.75となり、平行四辺形ABCDの面積は36だったから、面積の比は、36:3.75=48:5
いかがでしたか。
平面図形は描き方を工夫すれば簡単に解ける
相似と面積比の問題なのですが、図形を上手に描くことができれば、相似という知識を一切つかわなくても、三角形と四角形の面積の求め方を使ってこの問題を解くことができますね。
図形の問題を簡単に解くために必要な力は、実はどのように描けば解きやすいのかを工夫することなのです。
問題に描かれている与えられた図にただ線や数字を書き込むだけでなく、新たに解きやすく図を描くようにするともっともっと平面図形の問題が簡単に楽しく解くことができるかもしれません。
次回は暦の問題の裏ワザを紹介します。
図形の問題が続きましたので、次回は暦の問題をとりあげます。
奈良の名門・東大寺学園の2019年の問題です。どんな裏ワザが飛び出るのか、お楽しみに。
【問題】
西暦X年のカレンダーについて調べました。以下,〇/△で〇月△日を表すものとします。
(1) 西暦X年の2/1と8/1の曜日が同じでした。このとき,西暦X年の2/1,3/1,4/1,5/1,6/1,7/1,8/1,9/1,10/1,11/1,12/1の11日の中で,西暦X年の1/1と曜日が同じ日付を〇/△の形ですべて答えなさい。
(2) 西暦X年の6月のすべての水曜日の日にちの合計は65以下でした。このとき西暦X年の6/1の曜日として考えられるものをすべて答えなさい。
(3) (1)(2)のとき,さらに西暦X年の10月のすべての月曜日の日にちの合計は70以上でした。西暦X年の1/1は何曜日ですか
この連載のバックナンバーはこちら!








