こんにちは。中学受験算数ナビゲーターの滝澤です。
涼しくなってきたということは受験が近づいてきたということ
最近めっきり涼しくなり、ようやく秋が来たかと胸をなでおろしているところです。
しかし秋が来るということは、2025年度中学入試が近づいてくるということですね。
今年もやります。西暦の予想問題
さて、私としてはこの時期は頭をひねって問題を考える時期になります。
どんな問題というと、「西暦の問題」です。例年、様々な中学校の入試問題でその年の西暦の数字を題材にした問題が出されることがあります。これは予想しない訳にいきません。
実は2022年からもう3年連続でこのマガジンで西暦の予想問題を発表しています。
そして意外にも似たような問題を出題してくださる中学があるのです。
生徒や保護者の方から、「西暦の問題の記事を読んで、志望校の問題に正解することができました」という声も多くいただいています。
今年もがんばって予想しなくては!
来年は2025年です。
まずは「2025」という数の性質のうち、基本的なものを4つほど挙げておきましょう。
「2025」数の性質
- 45×45=2025 2025は45番目の平方数です。
- 2025を素因数分解すると3×3×3×3×5×5 約数は15個です。
- 81を4でわると20.25になります。これは2025の100分の1です。
- 2025は0と2と5の3種類の数字だけでできています。変則的な3進法と考えることができます。
これらのことを用いた問題も出題される可能性があります。おさえておきましょう。
2025には、これら以外にもいくつか面白い性質があります。今回は入試で出題されそうな問題を3問考えてみました。
第1問 九九にまつわる問題
九九とは1×1~1×9、2×1~2×9、3×1~……、9×1~9×9までの81個のかけ算のことです。これについて次の問いに答えなさい。
(1) 81個のかけ算の答えをすべてたすといくつになりますか。
(2) 81個のかけ算の答えのうち、同じ数字を1種類と考えると全部で何種類の答えがありますか。
いかがでしょうか。小学校の算数の基本の九九からの出題です。
さっそく解説をしていきましょう。
解説
(1) 九九の81個の答えをすべてたす式を考えてみると、
1×(1+2+3+4+5+6+7+8+9)+2×(1+2+3+4+5+6+7+8+9)+……+9×(1+2+3+4+5+6+7+8+9)
ですから、これをまとめると
(1+2+3+4+5+6+7+8+9)+(1+2+3+4+5+6+7+8+9)
になりますよね。ここで
1+2+3+4+5+6+7+8+9=45
ですから、九九の81個の答えをすべてたすと、
45×45=2025
となります。九九の81個の答えをすべてたすと2025になるんですね。
(2) これは直接2025には関係ありません。ていねいに調べていく問題です。
1~9まではすべてあります。これで9種類。
10~19では、10、12、14、15、16、18の6種類。
20~29では、20、21、24、25、27、28の6種類。
30~39では、30、32、35、36の4種類。
40~49では、40、42、45、48、49の5種類。
50~81では、54、56、63、64、72、81の6種類
9+6+6+4+5+6=36種類です。
50以上になると、突然少なくなるのは面白いですね。
第2問 立方数の和の問題
次のように規則的にならんでいる数があります。
1,8,27,64,……
次の問いに答えなさい。
(1) 9番目の数を求めなさい。
(2) 1番目の数から9番目の数までをすべてたすといくつになりますか。
次は規則性の問題です。まず、問題の数列の規則はおわかりでしょうか。
1×1×1、2×2×2、3×3×3……
という同じ数を3回かけた数(立方数)が並んでいますね。それでは解説していきましょう。
解説
(1) 9×9×9=729 これは計算するだけですね。
(2) まともに式を作ると次のようになります。
1+8+27+64+125+216+343+512+729
このくらいの計算であれば、最初からたしていってもいいのですが、もっと簡単な方法はないか考えてみましょう。それでもいくつかは試してみることが大切です。
1番目だけだと、1
1番目と2番目をたすと、1+8=9
1番目から3番目までをたすと、1+8+27=36
1番目から4番目までをたすと、1+8+27+64=100
1=1×1、9=3×3、36=6×6、100=10×10ですね。
1、3、6、10 この数列、有名な数列なのです。そうこれは三角数と呼ばれる数で、
1、1+2、1+2+3、1+2+3+4なのですね。9番目の三角数は
1+2+3+4+5+6+7+8+9=45 ですから、
1番目から9番目までをたすと、45×45=2025 となるわけです。
1からN番目までの立方数の和は、N番目の三角数の2乗(2回かける)になっているのですね。
第3問 覆面算の問題
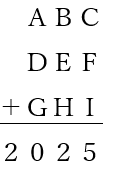
次のような筆算があります。A~Ⅰまでに1けたの数を入れて筆算が成立するようにします。ただし、
① C<B<A<D<G
② B<E<H
という条件が成り立っています。
A~Iまでの合計が異なるものを2種類答えなさい。
解説
この問題は毎年このマガジンで紹介している覆面算の問題です。この解き方は過去の記事も参考にしていただくとよいのですが、まずは、たてに並ぶ数の和について考える必要があります。
0から8までの和は36、1から9までの和は45ですから、A~Iまでの和は36以上45以下です。このことと、くりあがりがあることを考えて、
① A+D+G=19、B+E+H=12、C+F+I=5
② A+D+G=18、B+E+H=22、C+F+I=5
③ A+D+G=19、B+E+H=11、C+F+I=15
④ A+D+G=18、B+E+H=21、C+F+I=15
の4つの場合が考えられます。
ですから、A~Iまでの合計が異なるものを答えることが必要なのですね。
①の場合は合計が36ですから、0~8までの数を使い、②と③の場合は合計が45ですから、1~9までの数を使います。④にになると合計が54になってしまいますから、1~9の合計を超えてしまい、条件に合いません。あとは、数字をあてはめて考えていけば、それぞれ求めることができます。
答は一例です。
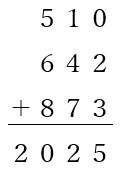
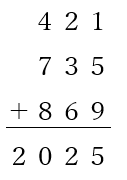
ぜひ問題を作ってみてください。
いかがだったでしょうか。
2025という数字はなかなか特徴の多い、面白い数字ですから、さまざまな問題を作ることが可能です。数字の問題をつくるのは、特別な準備は必要ありません。紙と鉛筆があればできます。皆様もぜひ暇な時間に2025にまつわる問題を作ってみてはいかがでしょうか。
面白い問題ができたらぜひ教えてください。
最後になりましたが、受験生の皆さんへ

受験生が一番成績を伸ばすことができるのは、秋から冬にかけて、すなわちこれからです。いくつか模擬試験を受けたり、過去問を解いたりして、時には思うように点数が取れないこともあるかもしれません。
けれど、だからこそ、少しでも日々の勉強の中に、知らなかったことを知る喜びや、気づくことができた楽しさをたくさん見つけられますように。自分の成長を信じてコツコツと頑張ってください。健闘を祈っています。
もし、入試問題でここに挙げた問題と似た問題がありましたらぜひ教えてください。
中学受験の対策講座はこちら
私が担当している講座では、自分で正解する力よりもわからない問題を自分なりにどう考えたかを説明する力をつけることを目標にしています。ご興味があればぜひお問い合わせください。お待ちしています。


一緒に楽しく中学受験をがんばりましょう!
(文責:滝澤幹)
「2025」問題、動画でも!
この記事で紹介した「2025」予想問題について、YouTube動画でも解説しています。
株式会社math channel代表の横山明日希&中学受験算数ナビゲーターのタキザワが解説するスペシャル動画を、ぜひご覧ください。
著者プロフィール

タッキー先生(滝澤 幹 たきざわ かん)
中学受験算数ナビゲーター
御三家筑駒中学受験専門塾にて指導歴30年。「算数の楽しさは正解だけではない」「すべての小学生に算数の難問を解く楽しさを知ってほしい」と思い、math channnelに参加。算数表現力ゼミを主催。共著書に『親子で楽しむ!中学受験算数』(平凡社刊)がある。
■こちらの連載もぜひどうぞ!
■タッキー先生が執筆に携わった本

中学受験算数で出てくる「つるかめ算や旅人算」などの特殊算について、線や図、表を使って視覚的にわかる本!
math channelマガジン編集長のぬまちゃん、株式会社math channel代表の明日希先生、そして中学受験算数ナビゲーターの滝澤先生3人による共著です。
異世界ストーリーを楽しみながら、つるかめ算や濃度算がすっきりわかる算数ファンタジーです!

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。
ぜひ、お手にとってご覧ください!












