こんにちは。中学受験算数ナビゲーターの滝澤です。
勝負の分かれ目は心の余裕

2023年も押し詰まって参りました。この時期になると中学受験を控えている6年生の皆さんは、模試の成績が上がらないとか、凡ミスが直らないなど苦しくなる頃です。
しかし、過去多くの卒業生が「合格作文」などで、「僕が(私が)本気になったのは12月(1月)になってからでした」という作文を残していますので、ここからが本当の勝負です。ここで分かれ目になるのは、実は「自分が楽しいと思えるかどうか」です。今やっている勉強を楽しむ心の余裕が必要かもしれません。
さらに、心の余裕を生むためには、体調が万全でなければなりません。睡眠時間、温度・湿度の管理、食事、運動そしてセルフチェックなど健康管理は万全に行っていただきたいと思います。
西暦の予想問題 3度目のチャレンジ

私としてはこの時期は楽しみながら頭をひねって問題を考える時期になります。
どんな問題か、それは、「西暦の問題」です。
例年、様々な中学校の入試問題でその年の西暦の数字を題材にした問題が出題されることがあります。これは予想しない訳にいきません。
一昨年はこのmath channel magazineで紹介した問題が見事2校(市川中学,渋谷教育渋谷中学)で出題されました。
しかし昨年は、まったく予想した問題は出題されませんでした。来年2024年はどうなるのか、2024に関する問題を4問考えましたので、ご紹介したいと思います。興味があればチャレンジしてみてください。
まずは一昨年の問題の数値替え
【問題】 次のように、3けたの整数3つのたし算を筆算で表したものがあります。
ア~クは1から9までの異なる整数とします。
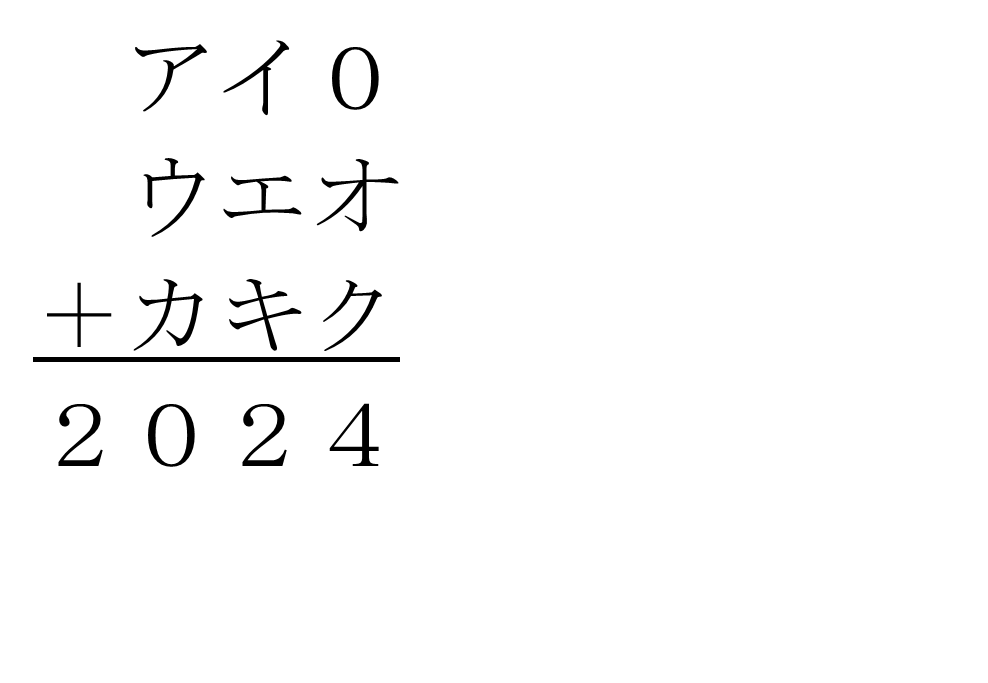
ア<ウ<カ
イ<エ<キ
オ<ク
であるとき、ア~クにあてはまる数を求めなさい。
(答えは2通りあります。)
一昨年に私が的中させた問題の数値替えです。答えが2022、2023のときと比べて、非常に少ない条件で答えがたった2通りにしぼることができましたので、これはなかなか面白いと思います。
ちなみに試しに大変算数の得意な1人の生徒に出題したところ、15分くらいで正解を出すことができました。
時間があれば是非挑戦していただきたいです。
解説
1~9までをすべてたした合計は45です。このうち、1~9までのいずれかの数がない訳ですから、
ア~クまでの8つの数の合計は36以上44以下となりますね。
そこで、筆算でたてにならんだ、ア+ウ+カ、イ+エ+キ、オ+クのそれぞれの和を考えます。
オ+クは4か14なので、場合分けをして考えてみましょう。
(1)オ+ク=4のとき
イ+エ+キは12か22となります。
① イ+エ+キ=12ならば、ア+ウ+カ=19 このとき、8つの数の合計は35となり不適
② イ+エ+キ=22ならば、ア+ウ+カ=18 このとき、8つの数の合計は44となる。
8つの数の合計が44ということは、1を使わないことになるが、オ=1に反してしまうため不適
よって、どちらも不適になってしまったので、オ+ク=14に決定しますね。
(2)オ+ク=14のとき(オ=5、ク=9、またはオ=6、ク=8)
イ+エ+キは11か21となります。
① イ+エ+キ=11ならば、ア+ウ+カ=19 このとき、8つの数の合計は44となる。(1を使わない)
② イ+エ+キ=21ならば、ア+ウ+カ=18 このとき、8つの数の合計は54となるので不適。
よって、イ+エ+キ=11で決定です。
このとき、(イ、エ、キ)は(2、3、6)か(2、4、5)の2パターンですね。
(オ、ク)は(5、9)または(6、8)なので、組み合わせると
イ=2、エ=3、オ=5、キ=6、ク=9
イ=2、エ=4、オ=6、キ=5、ク=8
の2パターンが考えられるわけです。
いよいよ大詰めです。
A:イ=2、エ=3、オ=5、キ=6、ク=9 のとき、
ア+ウ+カ=19で、残っている数字が4、7、8になりますから、
ア=4、ウ=7、カ=8ですね
筆算にすると次のようになります。
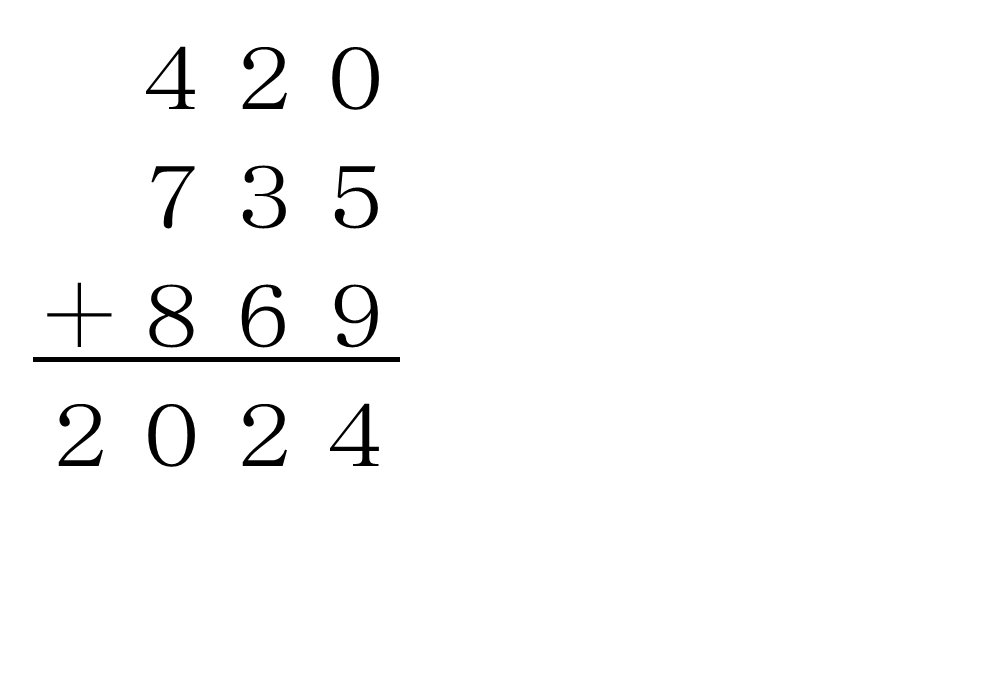
B:イ=2、エ=4、オ=6、キ=5、ク=8 のとき
ア+ウ+カ=19で、残っている数字が3、7、9になりますから、
ア=3、ウ=7、カ=9ですね
筆算にすると次のようになります。
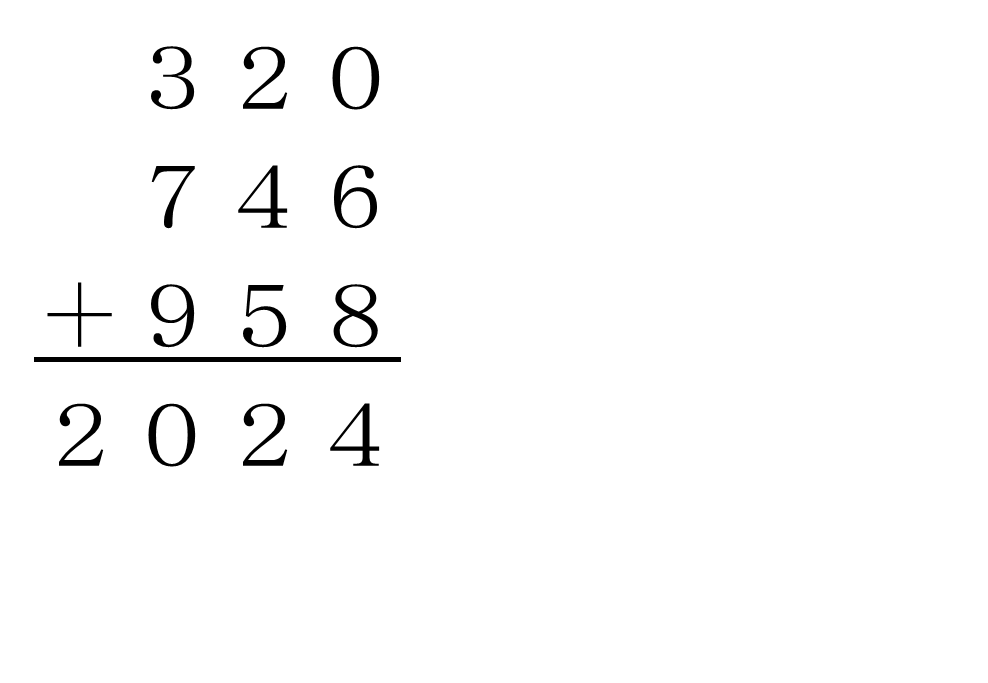
答え ア=4、イ=2、ウ=7、エ=3、オ=5、カ=8、キ=6、ク=9 または
ア=3、イ=2、ウ=7、エ=4、オ=6、カ=9、キ=5、ク=8
いかがだったでしょうか。当てずっぽうで解くとかなり大変ですが、まず合計がいくつになるのか?
それぞれの位ごとの合計はいくつになるのか?など順序を追って論理的に考えればおのずと正解に
たどりつける問題になっていたのではないでしょうか。
次は、約数などの基本から、流行りの問題までのセットです
【問題】 2024について次の問いに答えなさい。
(1) 約数のうち大きい方から5番目の数を求めなさい。
(2) 積が2024となる2つの2けたの数の組をすべて求めなさい。
(3) 2024をいくつかの連続する整数の和で表します。このとき初めの数とその個数の組をすべて求めなさい。ただし、10,11,12,13,14,15 のとき(初めの数が10で個数が6)は、(10,6)と答えなさい。
こちらは、流行りの連続する整数の和の問題です。
筑駒、開成などをはじめ多くの超難関国私立中学で出題されている問題ですね。
連続する整数の和は、約数に関係が深いということをしっかり理解しておきたい問題です。
解説
(1) 2024の約数をすべて書いてもよいのですが、少し面倒です。かといって、大きい方から
2024、1012、506、…と数えていくとミスをしそうですよね。この場合は実は小さい方から
5番目の数を考える方が楽ですしミスもしづらいのです。小さい方から5つ約数を書くと、
1、2、4、8、11ですよね。小さい方から5番目は11です。
実は小さい方から5番目の約数と大きい方から5番目の約数の積は2024ですから
2024÷11=184なので 大きい方から5番目は184と求めることができるのです。
答え 184
(2) (1)の続きの問題です。2024の約数を結局はすべて書いてみるとよいですね。
ただ、2024の約数をすべて書く場合も少し工夫して書くと、書き漏らしを減らせます。
1、 2、 4、 8、 11、 22、23、44
2024、1012、506、253、184、 92、88、46
わかりますか?たての2つの数を見ると、積が2024になっているのです。
こう書けば、答えが 22×92、23×88、44×46 になるのがわかりますね。
(3) 実は連続する整数の和の表し方が何通りあるかは、1以外の奇数の約数と関係があります。
2024の場合、奇数の約数は11、23、253の3つですから、3通りの表し方があるということです。
このとき奇数の約数は「連続する整数の個数」かまたは「平均(真ん中の数)の2倍」を表します。
11個のとき、真ん中の数が2024÷11=184 ですから、初めの数は179 (179,11)
23個のとき、真ん中の数が2024÷23=88 ですから、始めの数は77 (77,23)
253個だとすると真ん中が8になってしまいますが、負の数は算数では考えませんから、
これはありえません。よって、個数が16で、平均が253の半分の126.5ということになります。
よって初めの数は119 (119,16)
答え (179,11)(77,23)(119,16)
いかがでしょうか。連続する整数の和は解き方のパターンが明確ですから得点源になりやすいですね。
和が2024になるものは3通りしかありませんから入試問題としても出しやすい気がします。
自信作ですね(笑)。
今度は、連続した整数の積に関する問題です。
【問題】 3つの連続した数の積を考えます。例えば 5×6×7=210 ですが、
これを 【5】=210 と表すことにします。
次の問いに答えなさい。
(1) 【10】を求めなさい。
(2) 【A】=2730 のとき、Aの値を求めなさい。
(3) 【B】が2024で割り切れるとき、Bとして考えられる最も小さい数を求めなさい。
連続する整数の和に続けて、連続する整数の積についても1問作ってみました。
この問題は素因数分解に関係が深い問題ですね。2024の素因数分解はしっかりできるようにして
入試に臨みましょう。
解説
(1) これは小手調べです。答え 10×11×12=1320
(2) 2730=2×3×5×7×13 です。13という特徴的な素数から、これに連続する14や15を見つけ、
2730=13×14×15 とわかります。答え A=13
(3) 2024=2×2×2×11×23 です。23という特徴的な素数から、その隣の22や24を作れないかと考えます。
素因数分解を少し変形して 4×22×23 とすると、
22×23×24ならば2024の倍数になる とわかりますので、答 B=22
素因数分解から一歩進んで、2024をいろいろな積で表してみたときに、4×22×23ということに気づいた
ことから発想できた問題でした。23の倍数というのは出題されやすいポイントになるかもしれませんね。
最後に、典型的な「変形3進法」の問題です。
【問題】 次のように0、2、4だけを使った数を小さい順に書いていきます。
2、4、20、22、24、40、42、44、200、……
次の問いに答えなさい。
(1) 15番目の数を求めなさい。
(2) 2024は何番目ですか。
(3) これらの中で4の倍数だけを並べたときに、2024は何番目になりますか。
数字は0~9まで10種類ありますが、その中でいくつかの限られた数しか使わないという
ルールの問題もよく出題されます。これらの問題はN進法の問題として解くのが一般的です。
解説
(1) 0、2、4という3種類の数しか使わないので、3進法の問題です。
3進法は本来、0、1、2の3つの数字を使います。まずは3進法で15番目の数を求めてみましょう。
10進法の15は3進法で表すと15÷3=5あまり0、 5÷3=1あまり2ですから、
3×3すなわち9のまとまりが1つと3のまとまりが2つ、1のまとまりは0個となり、120となります。
しかし、今回は0→0、1→2、2→4と変換されますから、240が答えとなります。 答え 240
(2) 2024を本来の3進法で表すと、1012になります。
これは27のまとまりが1つ、3のまとまりが1つ、1のまとまりが2つですから、10進法に直すと、
27×1+3×1+1×2=32となります。よって32番目です。 答え 32番目
(3) 4の倍数の見分け方は下2ケタが4の倍数であることです。
さらに2ケタの数の4の倍数の見分け方は
十の位が奇数なら一の位は2か6。十の位が偶数なら一の位は0,4,8となります。
今回は使われる数字が0、2、4なので十の位は偶数ですから、一の位が0と4である数が
4の倍数ということになります。
2、4、20、22、24、40、42、44、200、……という数列は、4の倍数を〇、4の倍数でないものを×とすると、
×〇〇×〇〇×〇〇…と並んでいることがわかります。
2024は(2)から32番目でしたので、32番目までに〇が何個並んでいるかを考えればよいですね。
32÷3=10あまり2、ですから、10×2+1=21で21番目ということになります。答え 21番目
2024の問題を作ってみよう!
さていかがだったでしょうか。解けた解けない、簡単だった難しかった、いろいろあるかもしれませんが、
ぜひ1問でも2問でも2024を利用した問題を作ってみると良い勉強になると思います。
特に数の性質についてはよい復習になるのではないでしょうか。2024は2025より1小さいということは、44×46が45×45よりも1小さいことからも面白い問題が作れると思います。
入試直前だからこそ、必要なのは心の余裕です。そして、心の余裕とは、算数を楽しむ気持ちから生まれて
きます。出された問題を解くだけでなく、自分なりにアレンジしてみるとか、あらたに問題を作ってみるとか
、ふだんの学習と少し切り口を変えて、みると効果的に楽しい勉強ができるかもしれませんね。
(文責:滝澤幹)










