あけましておめでとうございます。
中学受験算数指導歴30年、主に筑駒中や御三家と呼ばれる最難関中学受験を専門にしたコースで算数を担当している滝澤です。
今年もmathchannelマガジンをよろしくお願いいたします。
さて、今年は2022年ですね。
中学入試の算数ではよく、その年の西暦にまつわる問題が出題されます。
昨年は2021という数が43×47の答えであることを利用した問題などが出題されました。
43と47はどちらも素数であり、「43でも47でも割り切れる~」という文章があると、「これは2021の倍数だな!」と考えながら解くわけですね。
(ということは、2022は「43でわっても47で割っても1あまる数」であることを使った問題が出題されるかもしれませんね!?)
2022の特徴をいくつか挙げると…
- 素因数分解すると2022=2×3×337であることを使った問題
(例えば、分母が2022の既約分数の個数など) - 0と2しか使われていないこと。例えば2進数や3進数の問題
- 各位の和が6であること。これは9で割った余りが6ということでもあります。
- 一番近い三角数は65番目の2045、一番近い平方数は45番目の2025
- 下2けたと上2けたで分けると、20と22になり2つ違い。積は440
2022を使った「虫食い算」に挑戦!
さてここでは、2022という数字を使った「虫食い算」に挑戦してみましょう。
正月で十分休息を取れた脳ミソにちょっと刺激を与えてみてはいかがでしょうか?
「虫食い算」という言葉はあまり聞いたことはないかもしれません。
たし算やひき算、かけ算、わり算の筆算で、いくつかの数字が空らんであるような問題を虫食い算といいます。
さて、ここでは中学受験指導歴30年の私・滝澤が、2022が筆算の答えとなる、今年の中学受験で出題されるかもしれない!?次のような虫食い算の問題をつくってみました。
クイズではなく、中学受験の問題として作ってみますので、その違いも感じていただければと思います。
では問題です!
下のようなたし算の筆算が成り立つようにA~Iの数字を求めます。
ただし以下のような条件があります。

- A~Iにはすべて異なる数が1つ入ります。
- Bは0です。
- FはAの2倍です。
- A<D<G、E<H、C<F<Iがすべて成り立ちます。
(「<」は右の方が左より大きいという記号です)
AとC~Iのに数字をあてはめて筆算を完成させましょう。
「クイズ」と「入試問題」の違いとは?
このままだと算数クイズの出題の仕方です。
クイズではなく入試問題を作るとすると、この問題を当てずっぽうではなく、できるだけ論理的に正解を導き出してもらいたいという中学校の先生方の考えが働き、「誘導(ゆうどう)」と呼ばれる、ヒントを兼ねた小問が出題されます。
例えばこんな具合です。先ほどの問題文の後、以下のように続きます。
(1) 次の計算の答えを求めなさい。
①A+D+G= ②E+H= ③C+F+I=
(2) 1~9の数のうち、使わない数字を求めなさい。
(3) 条件に合うようにAとC~Iに数字をあてはめて筆算を完成させなさい。

それでは(1)の問題を解説します。
①でA+D+Gは、十の位から1か2繰り上がることを考えて18、19、20あたりが候補になりそうですね。
次に、②のE+Hは異なる2つの1けたの数の和ですから、1+2=3、8+9=17より、その範囲は、3以上17以下です。
一の位から1か2繰り上がることを考えると、E+H=10か11か12となりますから、1繰り上がることが確実です。
これらのことから、A+D+G=19ということが決定しますね。
範囲を一つひとつ丁寧に考えよう
一方、C+F+Iは異なる3つの1けたの数の和なので、1+2+3=6、7+8+9=24より、その範囲は6以上24以下となります。
さらに一の位が筆算より2なので、C+F+Iは12か、22となります。
それでは、12と22のどちらか決めるためにはどうすればよいでしょう?
ここでA~Iまでの9つの数字の合計はいくつかを考えてみましょう。
(A+D+G)+(E+H)+(C+F+I)は、1~9のうち一つの数をのぞいた8個の数の合計です。
A+D+G=19、E+H=10か11か12なので、これら5つの数の合計は29か30か31となりますから、C+F+Iが22になることはありえません。
よって、C+F+Iは12となります。
一の位から1繰り上がるので、E+H=11となりますね。
(1)の答え ①A+D+G=19 ②E+H=11 ③C+F+I=12
(1)で考えたことをヒントにしよう
それでは(2)はどうでしょうか。
(1)で考えた1~9の9つの数の和は45ということがヒントになります。
A~Hまでで使っている数字の和は、19+11+12=42となりますから、使っていない数字は45-42=3ということがわかりますね。
(2)の答え 3
問題の条件はすべて使おう
(3)に進みましょう。
(1)(2)でわかったことから、それぞれあてはめていくのですが、ここでまだ使っていない条件があることを思い出しましょう。
FはAの2倍ですね。このことから、Aは1~4までとわかります(Aが5だとFは10になってしまいますから)。
さらに、Fは偶数であり、C+F+I=12いうことから、Fは5以下(Fが6になってしまうと、Iは7以上になって合計が13以上)ですから、 Aが1でFが2か、Aが2でFが4かのいずれかであることがわかります。
ゴールはもうすぐ!あてはめてみよう!
A+D+G=19ですから、A、D、Gにあてはまる数の組合わせは、A<D<Gより、
- (2、8、9)
- (4、6、9)
- (4、7、8)
- (5、6、8)
の4通りですが、Aは1か2なので、A=2、D=8、G=9と決定します。
ここでF=4も決まりますね。
E+H=11ですから、EとHにあてはまる数の組合わせは、E<Hより
- (2、9)
- (4、7)
- (5、6)
の3通りですが、2、4、8、9は使えませんから、E=5、H=6と決定します。
C+F+I=12ですから、C、F、Iにあてはまる数の組合わせは、C<F<Iより、
- (1、2、9)
- (1、4、7)
- (1、5、6)
- (2、4、6)
の4通りですが、残っている数字は1と4と7しかありませんので、C=1、F=4、I=7となります。
よって答えは
A=2、C=1、D=8、E=5、F=4、G=9、H=6、I=7
となります。
筆算にすると、このようになりますね。
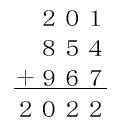
答えと同じくらい「途中の考え方」が大事
いかがだったでしょうか。
「正解だった!」「間違えてしまった……」などの結果が気になる人も多いかもしれませんが、最近の入試問題では、答えだけではなく、途中の考え方(過程)を問われる問題が増えています。
数をあてはめて、正解にたどり着くことももちろんとても大事ですが、一つひとつ論理を積み上げていくことがとても大事なのです。
「2022」という数の特徴を他にも考えてみた
2022を使った問題はこれ以外にもいろいろと考えられます。
この数の特徴をいくつか挙げると
- 素因数分解すると2022=2×3×337であることを使った問題
(例えば、分母が2022の既約分数の個数など) - 0と2しか使われていないこと。例えば2進数や3進数の問題
- 各位の和が6であること。これは9で割った余りが6ということでもあります。
- 一番近い三角数は65番目の2045、一番近い平方数は45番目の2025
- 下2けたと上2けたで分けると、20と22になり2つ違い。積は440
などなど。
これらの特徴を使ってどんな問題が作れるだろう?と考えてみるのも面白いですね。
最後に、2022にまつわる面白い計算を!
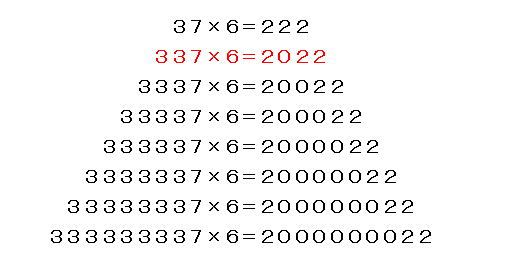
いかがでしたか。
今年はどんな西暦を使った問題に会えるのか、とても楽しみです。

実際に出題された2022年中学受験算数「面白い問題」ベスト3はこちら!
動画で2023年の予想問題を紹介しています!
(文責:滝澤幹)