こんにちは。中学受験算数ナビゲーターの滝澤です。
秋が深まってきました。
勉強もしやすい気候になりましたが、それはつまり2026年度中学入試が近づいてくるということですね。
受験生の皆さんは、秋の模擬試験がはじまり、志望校の過去問も解き始めているころではないでしょうか。
今年も「2026」に関する問題を考えます！（今年で５年目です）
さて、私としてはこの時期は頭をひねってある問題を考える時期になります。
それは、「西暦の問題」です。
例年、様々な中学校の入試問題で、その年の西暦の数字を題材にした問題が出されることがあります。
これを毎年このマスチャンネルマガジンで予想問題を発表しているのです。
なかなか百発百中というわけにはいきませんが、昨年も１問、「九九の81個の答の和が2025である」
という問題が的中しました。今年もこりずに予想したいと思います。
なぜなら楽しいからです。算数の問題作るの楽しいんですよ。
来年は2026年です。
というわけで来年の西暦は「2026」。昨年は2025という極めて特徴的な整数だったのですが、
2026はあまりこれといった性質がありません。
それでもいくつか2026の数の性質を紹介しておきましょう。
① 各位の数の和が10である。
2＋0＋2＋6＝10 になりますね。さらにこの10を同じように各位の和を求めると１になります。
② 各位の数を２乗してそれらをすべてたすという操作を繰り返し行うと１になる。
まず、１回操作を行うと、2026→2×2＋0×0＋2×2＋6×6＝44
さらにこの操作を繰り返すと、44→4×4＋4×4＝32
32→3×3＋2×2＝13
13→1×1＋3×3＝10
10→1×1＋0×0＝１ となって、最終的に1になります。
このような性質をもつ数には、「ハッピー数」という名前がついています。
③ 2025に1をたしたものである。
2026＝2025＋1になります。当たり前のようにも思えますが、2025＝45×45ですから、
2026＝45×45＋1×1であるということになります。
2026自体が、２つの平方数の和になっているんですね。
④ 2026の半分の1013も2つの平方数の和で表すことができる。
2026の半分は1013です。1013＝22×22＋23×23
とこちらも２つの平方数の和で表すことができます。
共通テーマは２乗（平方数）の和？
①②はともかく、③④は絞り出した感がありますね。
2026という数字はあまり特徴がない数ですが、こうしてみると、２乗の和に関するものをいくつか見つけることができました。
２乗の和と言えば、三平方の定理も思い出すことができますね。これらのことを用いた問題も出題されたら面白いですね。
今年は３問作ってみました。さっそく参りましょう。
問題編
第１問 虫食い算
下のア～キには、それぞれ異なる０、２、６以外の整数が入ります。
この筆算が成り立つような４けたの数アイウエのうち、
最も小さい数を求めなさい。
第２問 場合の数
2026は各位の数の和が10になる整数です。同じように各位の数の和が10になる
整数を小さい順に並べていくことを考えます。次の問いに答えなさい。
(1) 30番目の数は何ですか。
(2) 2026は何番目の数ですか。
第３問 平面図形
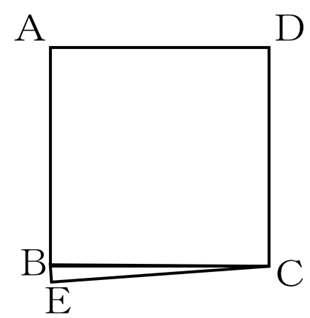
次の正方形ＡＢＣＤの面積を求めなさい。ただし、BE＝1cm、CE＝45cm、角BECは直角です。
解答解説編
第１問 虫食い算
ア～キに入る数は、1、3、4、5、7、8、9のいずれかです。この中で最初にわかるところがありますね。
そうです。くり上がるだけですからア＝１です。
残りはイ～キで、残っている数字は3、4、5、7、8、9です。
筆算を見ると、エ＋キ＝６、ウ＋カ＝２、イ＋オ＝10のように見えます。合計18ですね。
3、4、5、7、8、9の和を計算すると36になります。１回くりあがると、数の合計は９
減りますから、一の位と十の位もくりあがりをしているということになりますね。
つまり、
イ＋オ＝9
ウ＋カ＝11
エ＋キ＝16
ということがわかります。それぞれあてはまる数を考えてみると、
エとキがまずわかりますね。7と9になります。残った数字も
イとオは4と5、ウとカは3と8ということがわかります。
最も小さい４けたの数アイウエを求めるので、答えは1437
第２問 場合の数
(1) まず2けたの数で各位の和が10になる数を小さい順に書いていきましょう。
ここまでで9つあります。
19、28、37、46、55、64、73、82、91
次に3けたの数のうち、百の位が1で各位の和が10になる数を小さい順に書いていきます。
109、118、127、136、145、154、163、172、181、190
ここまでで全部で19個になります。30個まではあと11個です。
次は百の位が2で各位の和が10になる数を小さい順に書いていきます。
208、217、226、235、244、253、262、271、280
ここまでで全部で28個。次は百の位が3ですから、
307、316 よって答は316です。
(2) (1)から、2けたの数は9個、3けたの数のうち、百の位が1の数が10個、
百の位が2の数が9個ということがわかっています。
ということは３けたの数の場合、百の位の数が1増えるごとに、個数が1ずつ減っていくということです。
確かに、百の位の数が9の場合、901と910の2個ですね。
よって、3けたの数は、
10＋9＋8＋7＋6＋5＋4＋3＋2＝54
で54個であることがわかります。
次に1000～1999の数のうち、各位の和が10になる数を考えます。
ということは百の位と十の位と一の位の和が9になる数を考えることになりますね。
009、018、027、036、045、054、063、072、081、090、ここまでに10個
108、117、126、135、144、153、162、171、180 この列は9個
207、216、225、234、243、252、261、270 この列は８個
……
やはり、１個ずつ減っていくことがわかります。
つまり10＋9＋8＋7＋6＋5＋4＋3＋2＋1＝55
よって、1000～1999の数のうち、各位の和が10になる数は55個です。
最後に、千の位が2で各位の和が10になる数を小さい順に書いていくと、
2008、2017、2026
となりますから、
9＋54＋55＋3＝121番目が答となります。
別解もありますが、小学生にはなかなか理解しづらいかもしれません。
１～999までに各位の和が10になる数は、〇を10個としきりのたて棒｜を２本を並べること
で表すことができます。例えば、〇〇〇｜〇〇｜〇〇〇〇〇なら、〇の数が左から3、2、5なので、325と考えるわけです。｜〇｜〇〇〇〇〇〇〇〇〇なら、０、１、９なので19です。
すると、全部で〇と｜合わせて12か所からしきりのたて棒｜が入る2か所を選ぶ
組み合わせを考えればよいので、
12×11÷（2×1）＝66通りとなります。
しかし、各位の数は9までしかないので、〇が10個連続で並ぶ3通りは除きます。
よって、１～999までで、各位の和が10になるのは63通りです。
次に千の位が1の4けたの数で、各位の和が10になるのは、同様に考えると1～999までで、
各位の和が9になる数が何個あるか考えればよいですね。
よって、〇が9つと｜が2つを並べればよいので、11か所から2か所を選ぶ組み合わせで、
11×10÷（2×1）＝55通り
あとは、2008、2017、2026の3通りなので、
63＋55＋3＝121番目となります。理屈がわかればこちらの解き方の方が簡単ですね。
第３問 平面図形
図のように、正方形ABCDの内部に三角形BECと合同な直角三角形を4つ書き込みます。
すると中央に正方形ができます。この正方形の1辺は、45－1＝44cmです。
よって、正方形ABCDの面積は、直角三角形4つと1辺44cmの正方形の面積の合計
ですから、
1×45÷2×4＋44×44＝2026cm2です。
まだまだ考えられそうです。問題募集します！
以上３問ご紹介しました。どの問題も難易度としても適度ですので、挑戦してもらえると
うれしいです。ハッピー数の問題も作ったのですが、例えば
「2026はハッピー数ですが、2026に最も近いハッピー数はいくつですか？」
などという問題はいかがでしょうか。他にもまだまだ考えられそうです。
問題を考えるのはとても楽しいので、ぜひ皆さんにも挑戦してみてほしいです。
いい問題がいくつか集まったら、ここでご紹介しても面白いなと思いました。
ぜひ編集部あてに送ってください。お待ちしています。
（文責：滝澤幹）
『線と四角と表でわかる つるかめ算』（日東書院本社）発売中！
「つるかめ算」「和差算」「濃度算」「旅人算」などの特殊算を図解で解説している本『線と四角と表でわかる つるかめ算』（日東書院本社）が発売中です！
