ずーさん
ずーさんずーさんの『だったら算数ナゾトキ!』のページへようこそ!
この記事は、
小学生のみんなに楽しく算数にふれてほしい算数ナゾトキ★クリエイターのずーさんが、
①何かよい自学(自主学習)の算数ネタってないかな??
②もうちょっとゲームっぽく取り組める算数の問題ないの??
③ちょっとだけ、かるーく、予習できたらいいな!
の声にお応えして、
 ずーさん
ずーさんだったらコレ!算数ナゾトキ!
ということで謎解きの問題を、出題&解説しちゃいましょう!
そして、さらに!
今お読みいただいているパパママ、もしくは小学生のみんなとナゾトキを作成しちゃいましょう!というものです♪

「円」をかるーくおさらい!
今回のナゾトキは小3であつかう単元にかかわるものです。
必要となる知識があるので、小2以下の読者のためにもさらっと今回のテーマである「円」についてお話しておきましょう。
どうぞみなさん、紙の上のまんなか辺りに、点を1つかいてみて下さい。この点を「きほんの点」とよぶことにします。正しくまんなかでなくても、だいたいで大丈夫です。頭の中で想像するだけでもかまいませんよ。

次に、「きほんの点」から4㎝はなれたところに、また点をかいてください。ものさしを使って4cmをはかれますか?

そして、さらにもう1つ、「きほんの点」から4㎝はなれたところに点をかいてみましょう。2つもあるのかと思うかもしれませんが、頑張ってみつけてみてください。必ずありますよ!

さらに!あと3つかけますか?さあ、ものさしをななめにしましょう。実は「きほんの点」から4㎝はなれた点はまだまだあるのです!
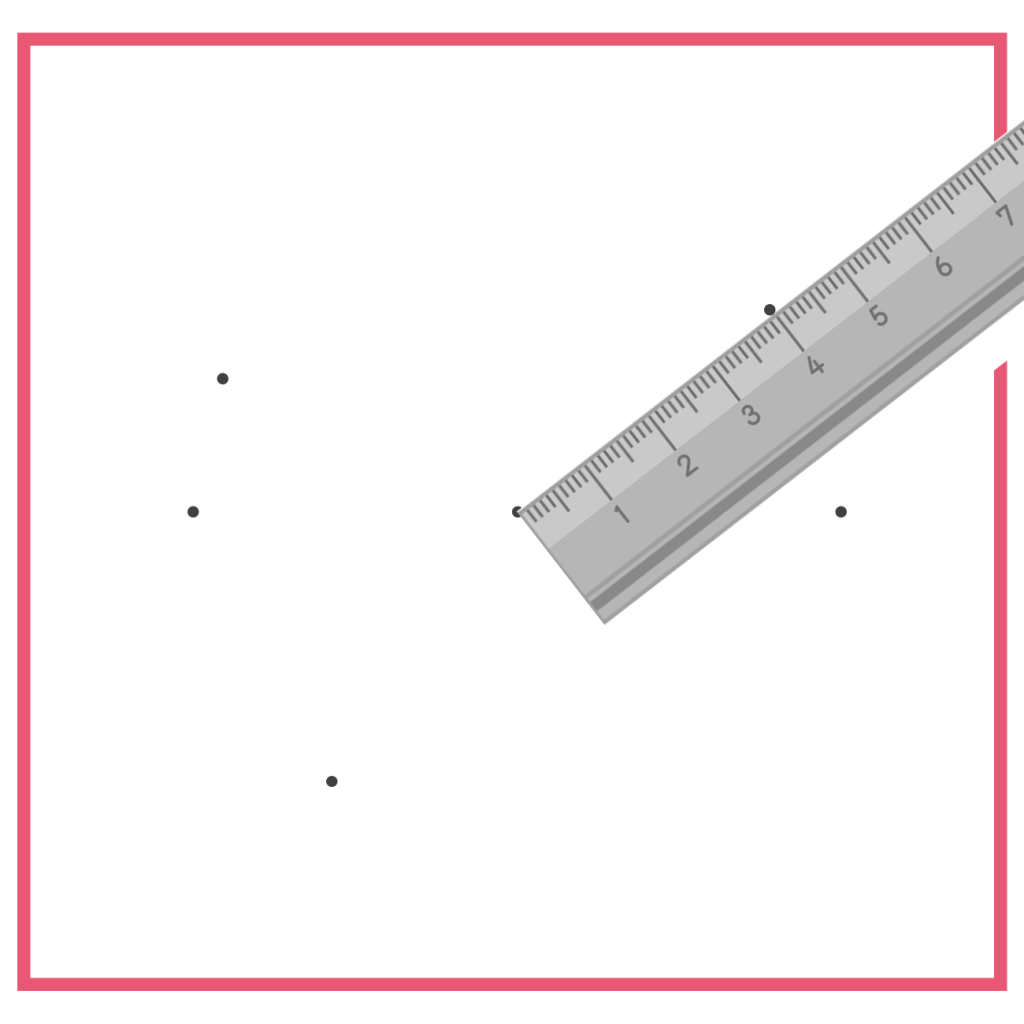
もっともっとかいてみてほしいのですが、たくさん書くとどんなカタチができるか、わかりますか?まだよくわからないぞという人は、少しずつずらしながら、あと5つかいてみましょうか。

丸い形が見えてきたのではないでしょうか。
このように、ある点から同じキョリにある点の集まりを「円」といいます。
今回の場合でいえば、「きほんの点」から4㎝のキョリにある点の集まりですね。
そして、「きほんの点」のことを「円の中心」、4㎝の長さのことを「円の半径」といいます。
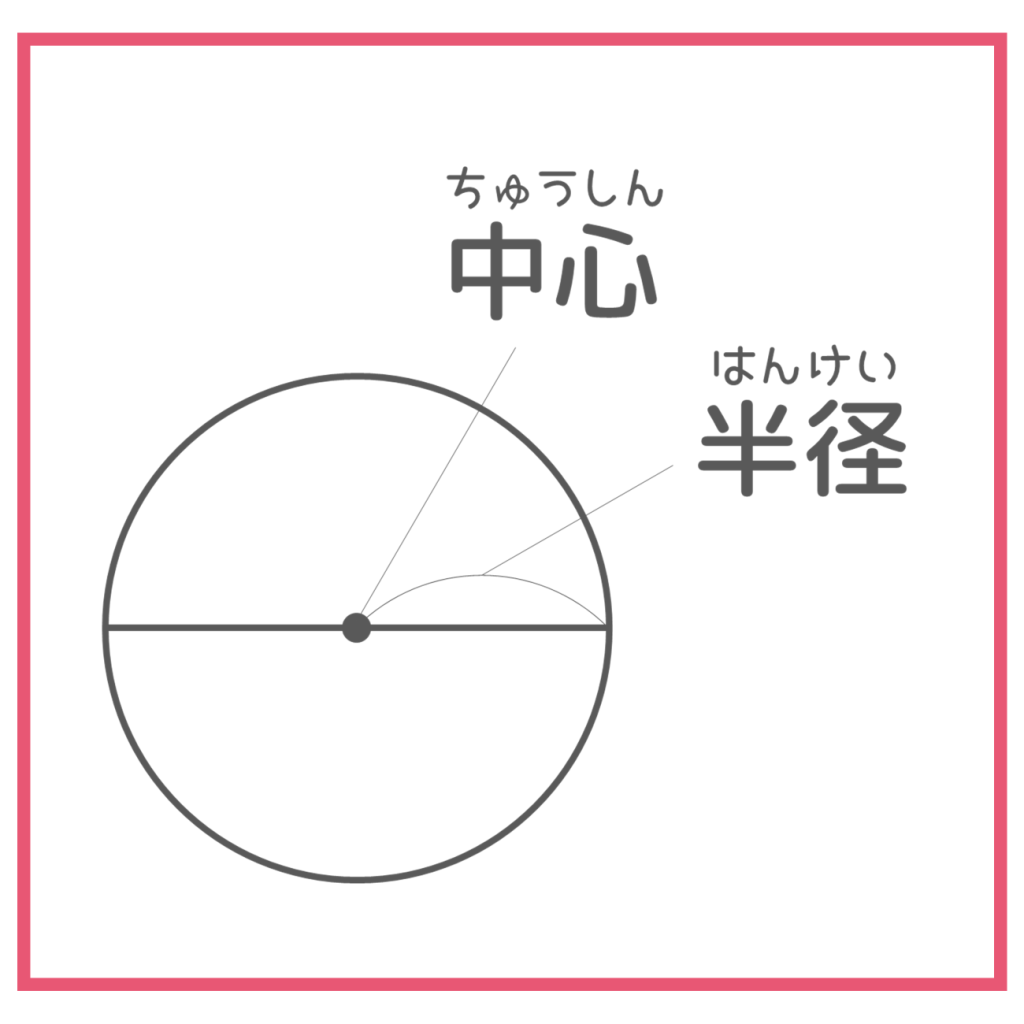
また、4㎝はなれた点でできた線を「円周」、その円周の1つの点から「円の中心」を通る直線をひいたとき、反対側の円周とぶつかるところまでの長さを「円の直径」といいます。
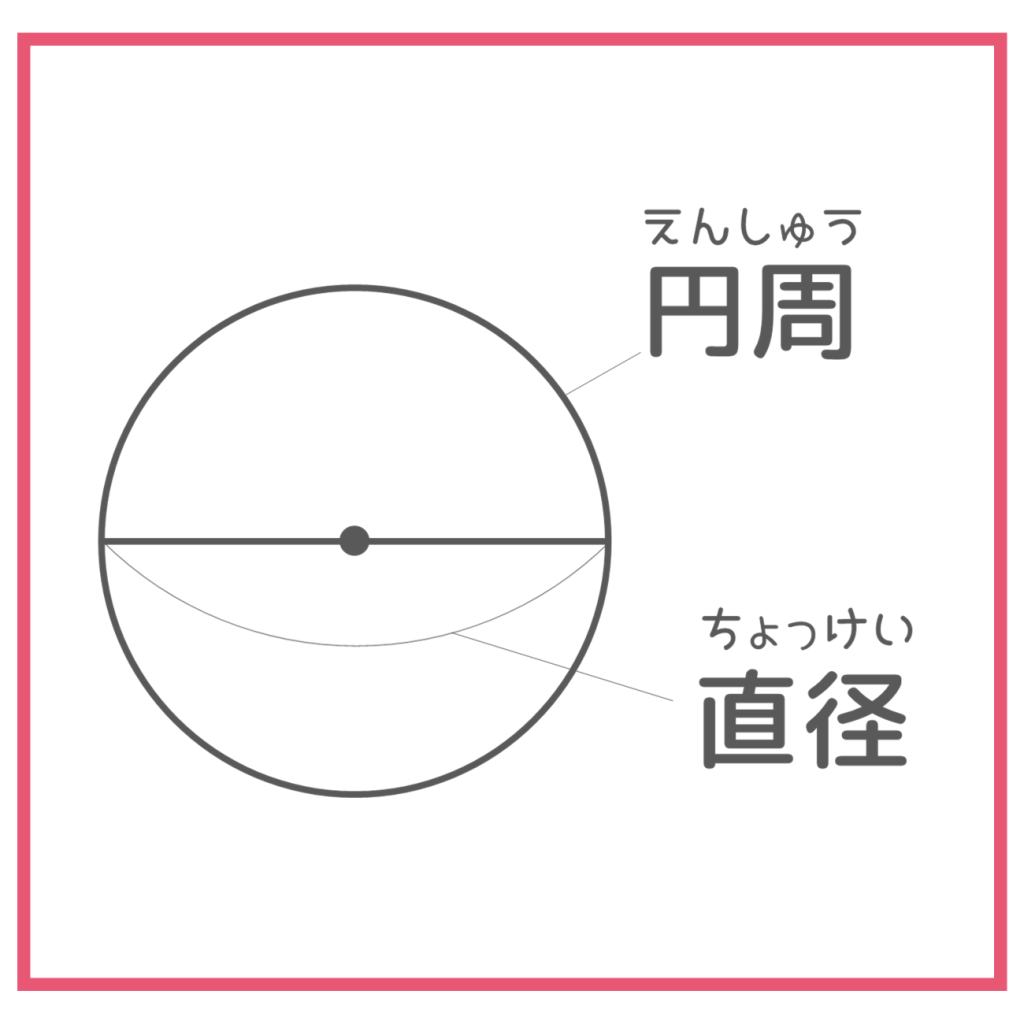
こんな風に、円についてはいろいろ名前が決まっているので、この先「円周」「中心」「半径」「直径」がどこの部分のことかわからなくなったら、上の2つの図を見てくださいね!
便利な道具、コンパス!
ところで、円をかこうと思ったら、いつも先ほどのようにたくさん点をかきまくらないといけないのでしょうか?ちょっと大変ですよね。実は、とてもいい道具があるのです!それがこちら!

コンパスという道具です。棒人間の脚みたいな姿で、2本の脚の開き具合を変えることができます。
脚の一方の先(写真では左)は針で、もう片方(右)は鉛筆やシャーペンなどの筆記用具がついています。
どうやって使うかわかりますか?
たとえば、先ほどと同じように半径が4㎝の円をかくのだとしたら…
- コンパスの脚を4㎝の幅に広げます。
- 円の中心にしたいところに針を置きます。
- あとは筆記用具の方を紙に付ければ中心から4㎝はなれた点が打てるので、そのまま、隣にもかき、そのまた隣にもかくようにすべらせれば、円が完成します。
 ずーさん
ずーさんこれがあれば、まあるい線をきれいにかけます!
日常でも脚のことをコンパスって言ったりするよね。
ずーさんはよく「缶けり」という遊びをするときに自分の左足を針にしてしゃがみ、のばした右足で円をかいてました(缶けり知ってるかな~?)。
今回のナゾトキ〈作成編〉ではこのコンパスを使用します!
が、その前に謎を出題しましょう~!
問題
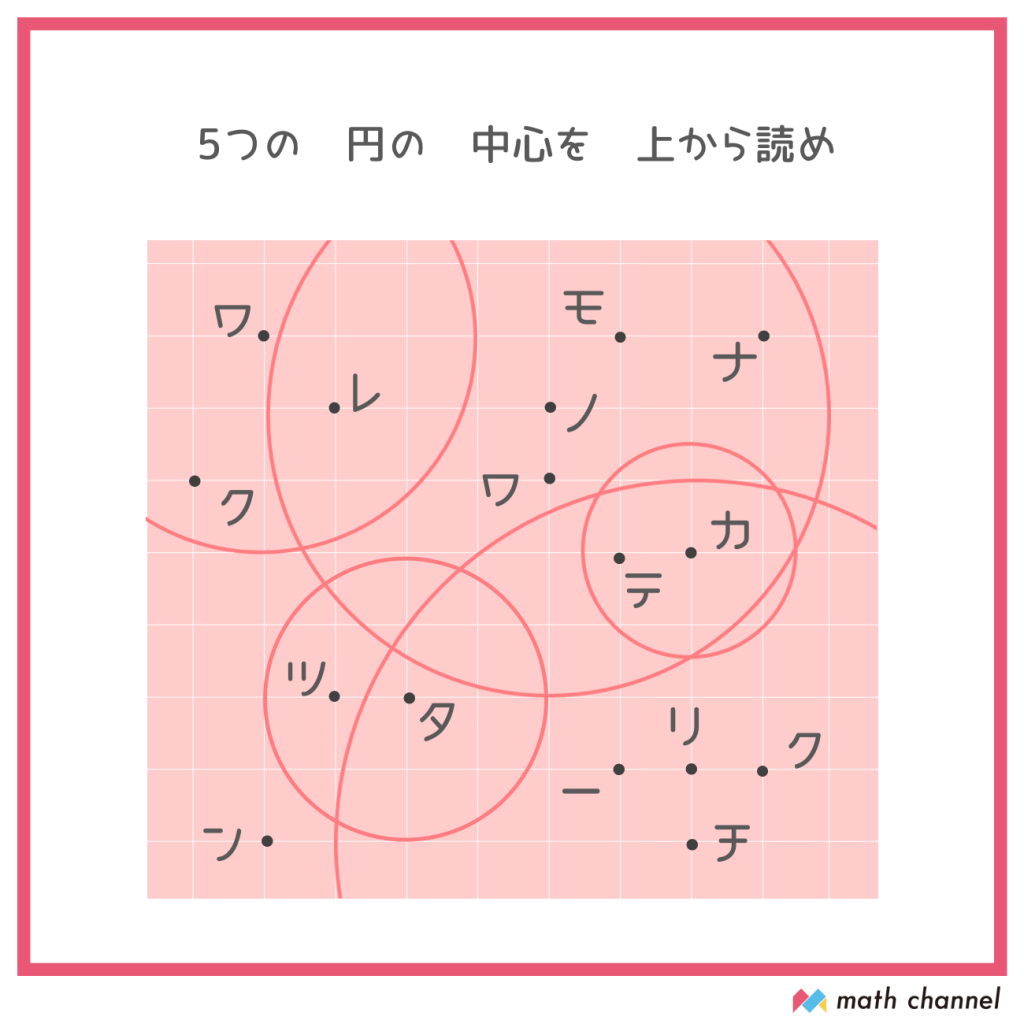
↓注意(ちゅうい)!この下にヒントがあります↓
ヒント1
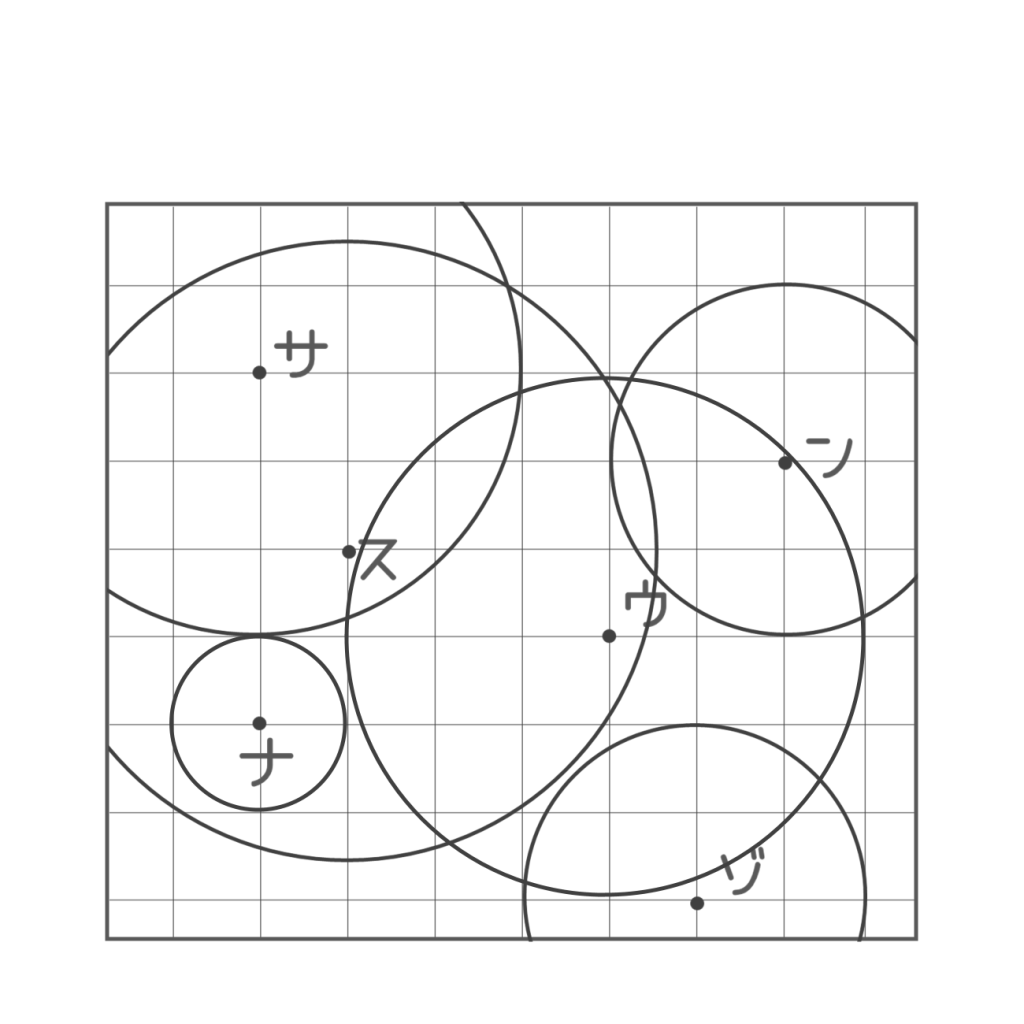
まずは5つの円(3つは一部)をすべてみつけてみましょう。
↓次のヒント↓
ヒント2
みつけた円の中からひとつ決めて、その中心だと思える点を選びましょう。円の中心はその円の中にあるはずですよ。もし違っても大丈夫! 選びなおせば良いだけなので、まずはどれか選んでみてください!
その選んだ点が本当に円の中心なら、そこから円周までのキョリはどれも同じはずです。でも、円周までのキョリはどうやってくらべたらいいでしょうか……?
↓次のヒント↓
ヒント3
ものさしをあてるのは難しいですが、マス目がありますね!
中心(と思われる点)からまっすぐ上やまっすぐ下、あるいは左右であればマス目の数で長さを表せそうです。
では、実際に数えてみましょう。
中心だと思う点からまっすぐ上にいったとき、円周までの点は何マスくらいになりますか?上の方に円周がない場合はまっすぐ下にいって数えてみましょう。ぴったり何個分では表せないかもしれませんが、そんなときは「3マスと半分」などと覚えておいたら大丈夫です。
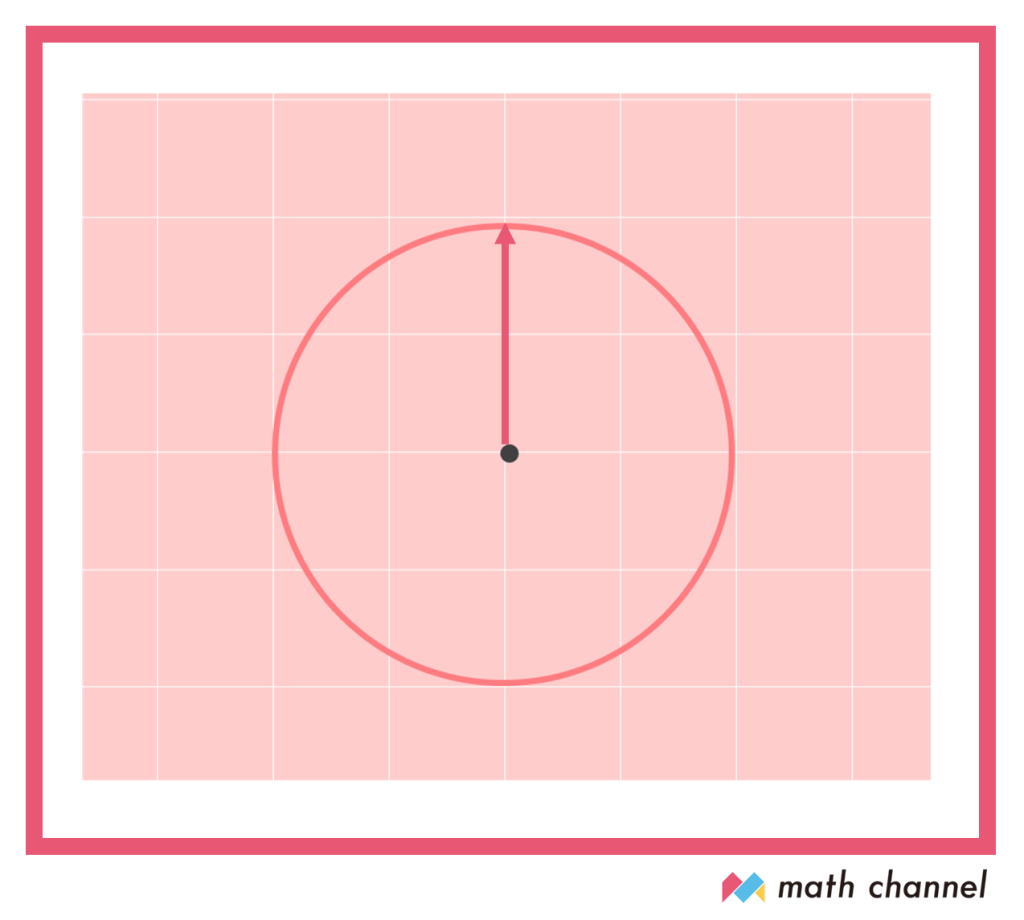
次に、左か右についても調べます。
ここで、上下と左右、2回はかった長さが同じなら、それは円の中心である可能性があります!そして、3回はかってどれも同じ長さなら絶対に中心です。
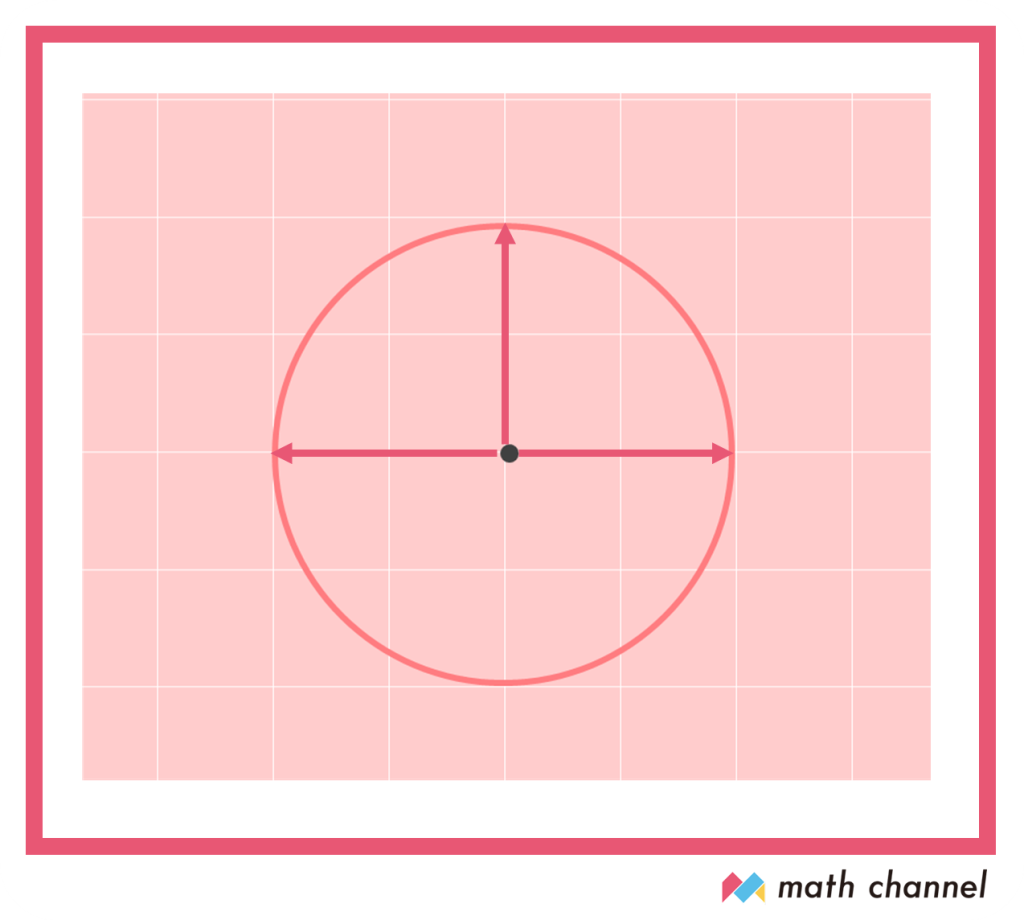
 ずーさん
ずーさんやったね! 中心を見つけたぞ!
2回や3回はかった場合に違う長さがあった時は、残念ながら中心ではないので別の点を選んでもう一度調べてみてね。
困るのは、上下左右のうち2回しかマスの数を数えることができない点の場合ですが、
そんな時は、円周をよくみてみましょう。
例えば、えらんだ点からまっすぐ上にたどった時、出発の点が本当に円の中心であれば、終わりの円周の点は必ず他の円周の点より上の位置にあります。山の頂上のようなイメージです。
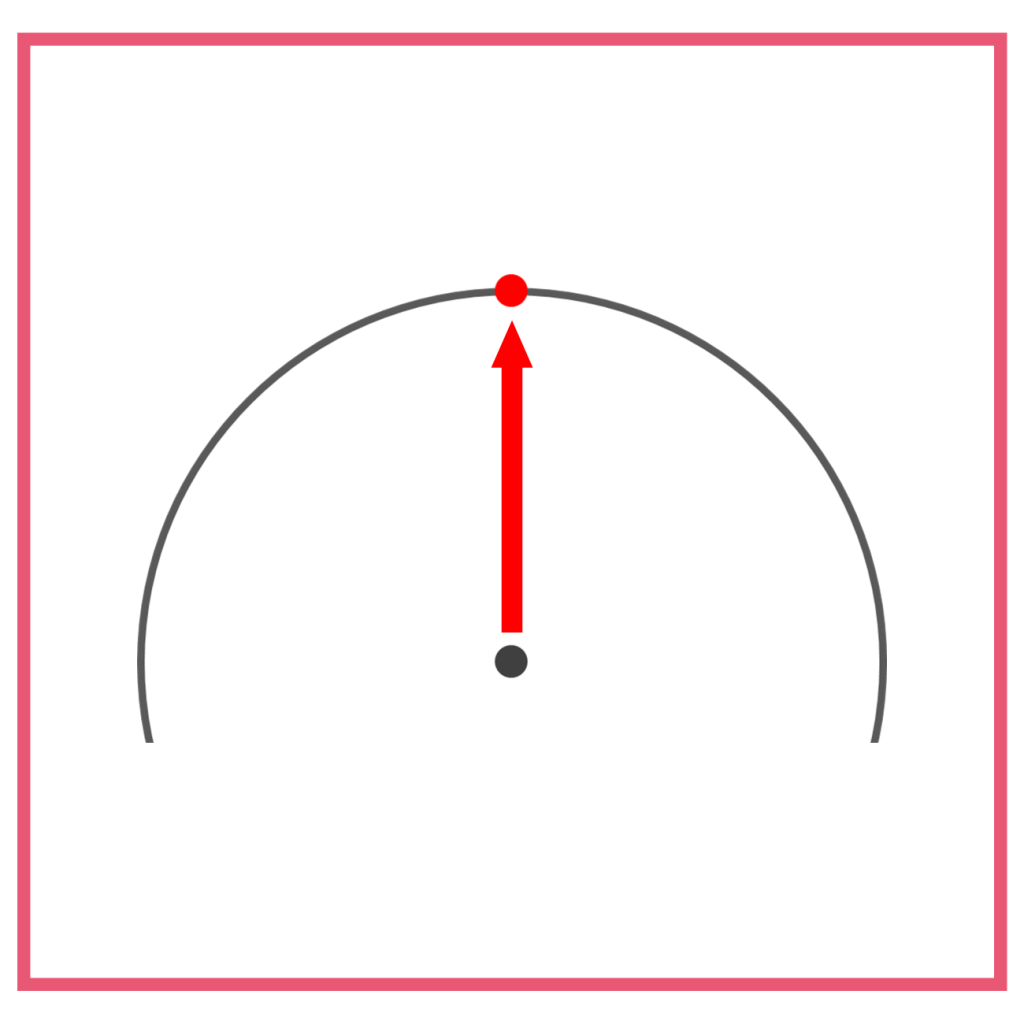
中心と思われる点からまっすぐ下にはかるのであれば、終わりの円周の点はまわりよりも下にあります。右にはかるなら、まわりよりも右になっているか、左にはかるならまわりよりも左であるかをみればいいわけです。
もし違った場合は、円の中心ではなかったということなので、他の点を選んでまた調べてみましょう!
↓次のヒント↓
ヒント4
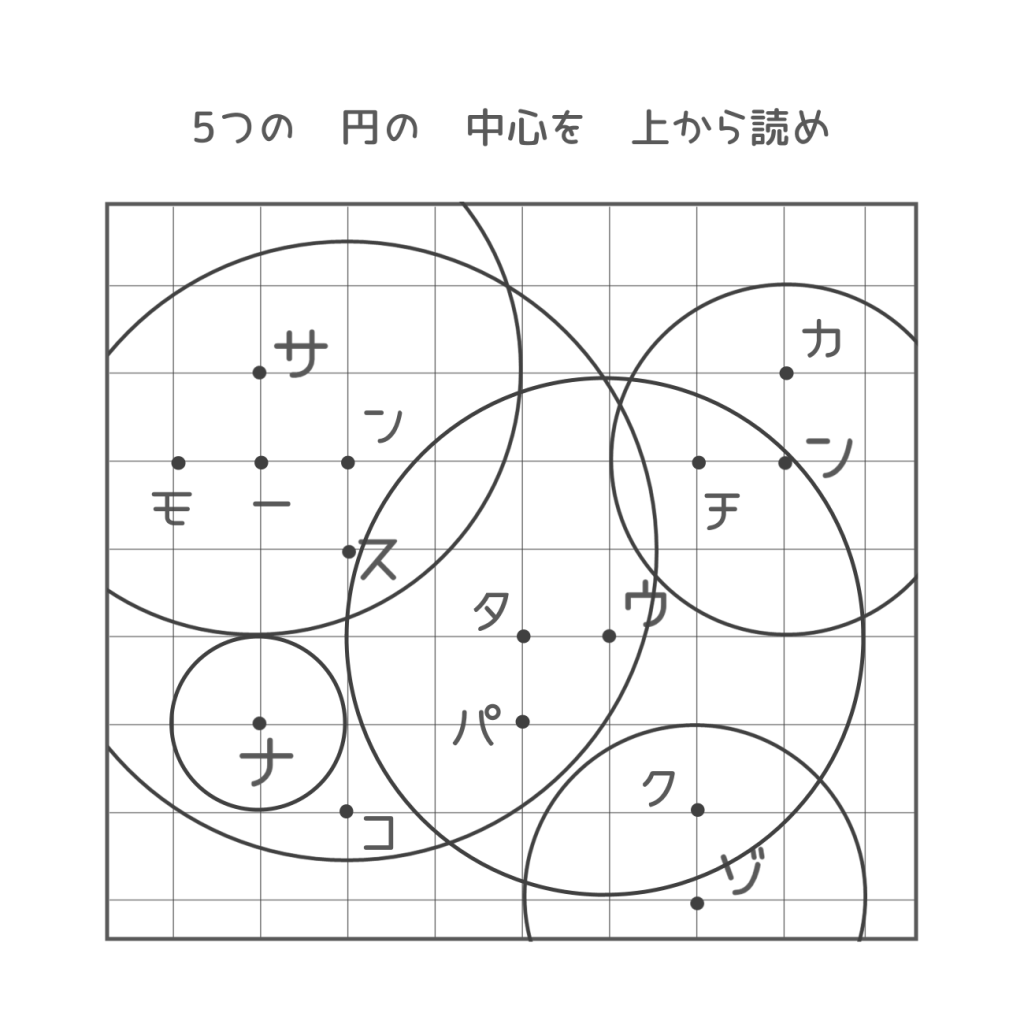
同様に、5つの円についてその中心を探します。みつけたら、文字と一緒に囲っておきましょう。全部みつけて上から文字を読むと……?
↓この先に解答と解説があります↓
解答

答えは「ワノカタチ」(輪の形)でした!
できましたか?
解説
といっても、解き方はほぼ「ヒント」で説明してしまいましたのでそちらをご覧ください。
ここではそれぞれの円についてまとめておきましょう。
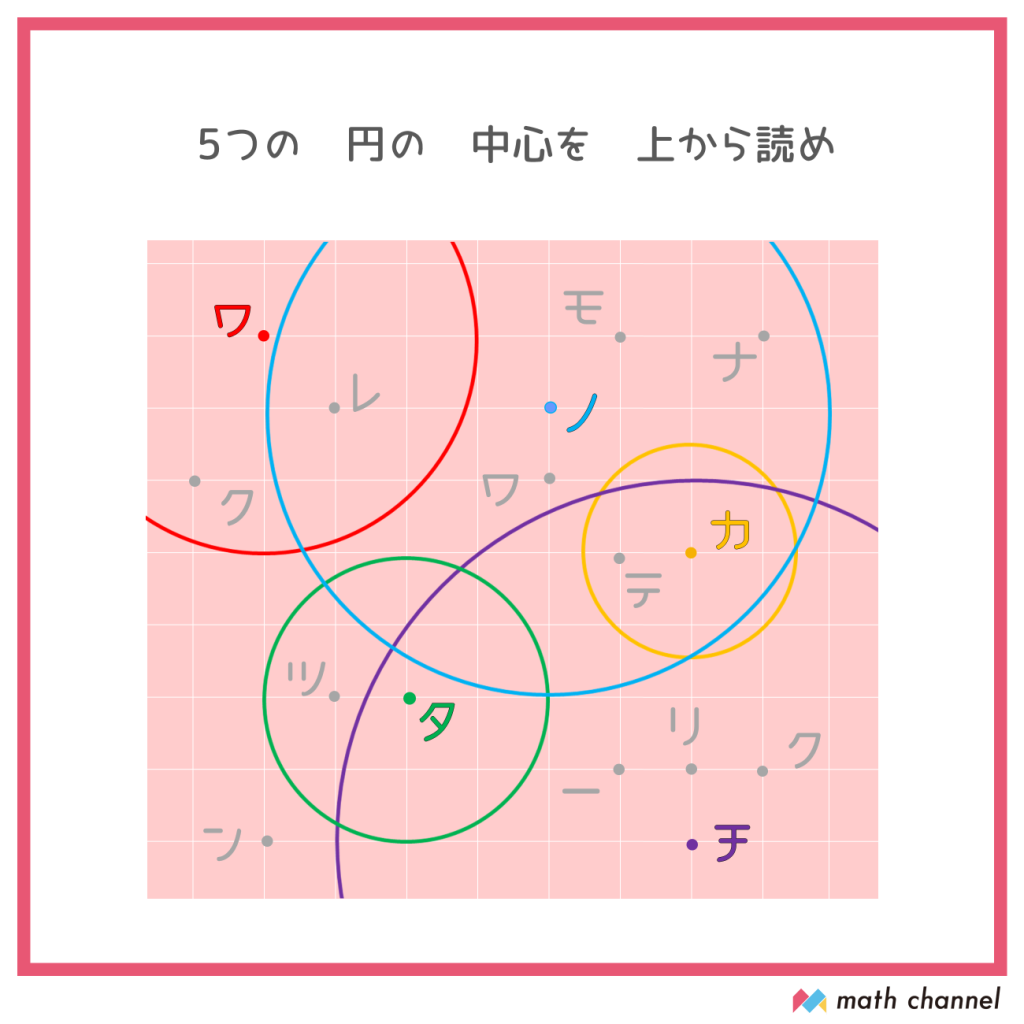
赤い円の中心は「ワ」の点、半径は3マス分
青い円の中心は「ノ」の点、半径は4マス分
黄色い円の中心は「カ」の点、半径は1.5マス分(1マスと半分)
緑の円の中心は「タ」の点、半径は2マス分
紫の円の円の中心は「チ」の点、半径は5マス分
でした!
見た目はごちゃごちゃしていますが、1つ1つ順番に注目する円を定めて中心をみつけてもらえたら答えにたどりつけるかと思います!
つくってみよう!
さあ、では次は、この謎を一緒に作ってみましょう!

 ずーさん
ずーさんこの単元が「ちょっと苦手だな。」というお子さんには、どうぞパパママが作って類題にしてあげて下さい。
「自学としてやってみたい!」というお子さんは、ずーさんとレッツ・トライ!
作成にはこちらのPDFを印刷すると便利です。
手順(てじゅん)1
まずは方眼用紙を用意しましょう!
小学生のみなさんはノートにマス目がもともとあると思うので、そちらを上手く利用してください!
手順2
次に、答えにしたい言葉を決めましょう。4~6文字の単語がおすすめです。
 ずーさん
ずーさんフランス、スロバキア、アルゼンチン……
たこやき、きなこもち、ちょこれーと……
なんでもOK!
決めたら、方眼のわかりやすいところ(交点)に答えの文字の数だけ点をうち、
上の点からそのそばに文字をかきます。
今回は答えを「算数ナゾ(サンスウナゾ)」にして、6文字で説明しますね!
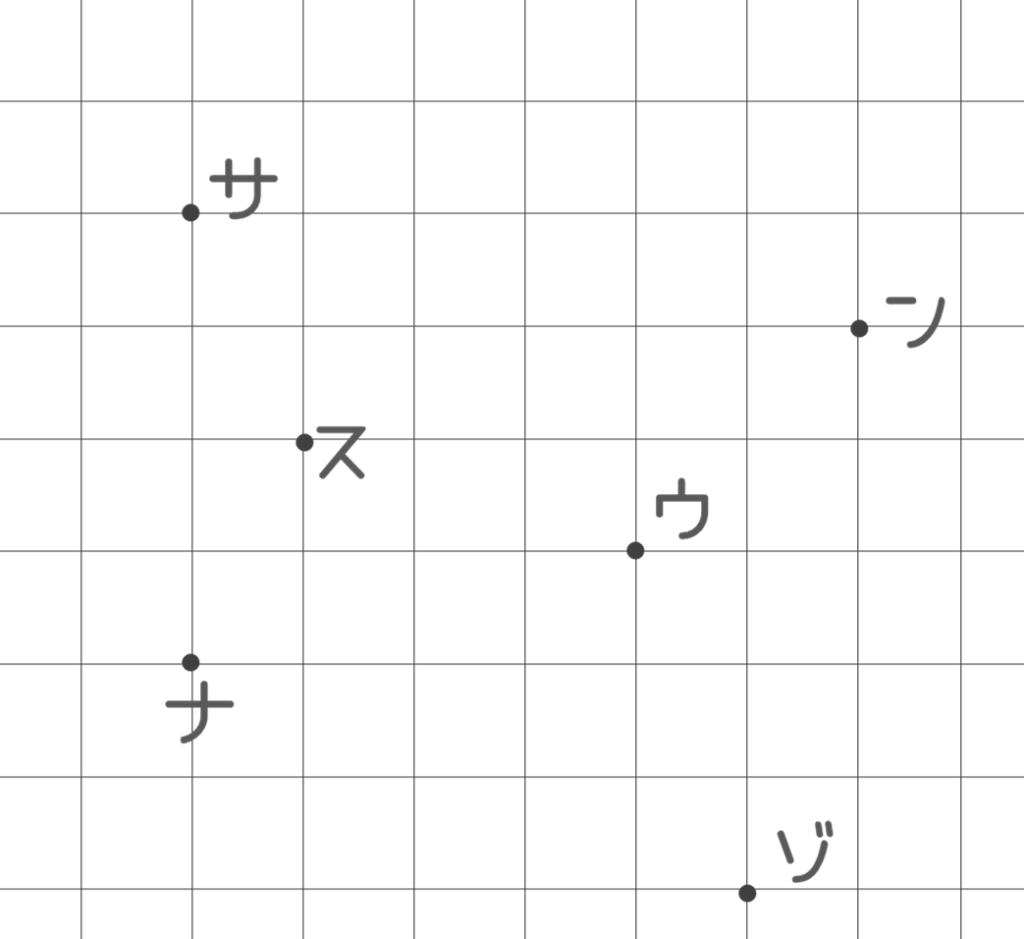
手順3
さあ、いよいよ円を描いていくのですが、先にどこまでを描く範囲にするか決めて、四角い枠を描いてしまった方が楽かもしれません。これは絶対ではないのでお好みで!
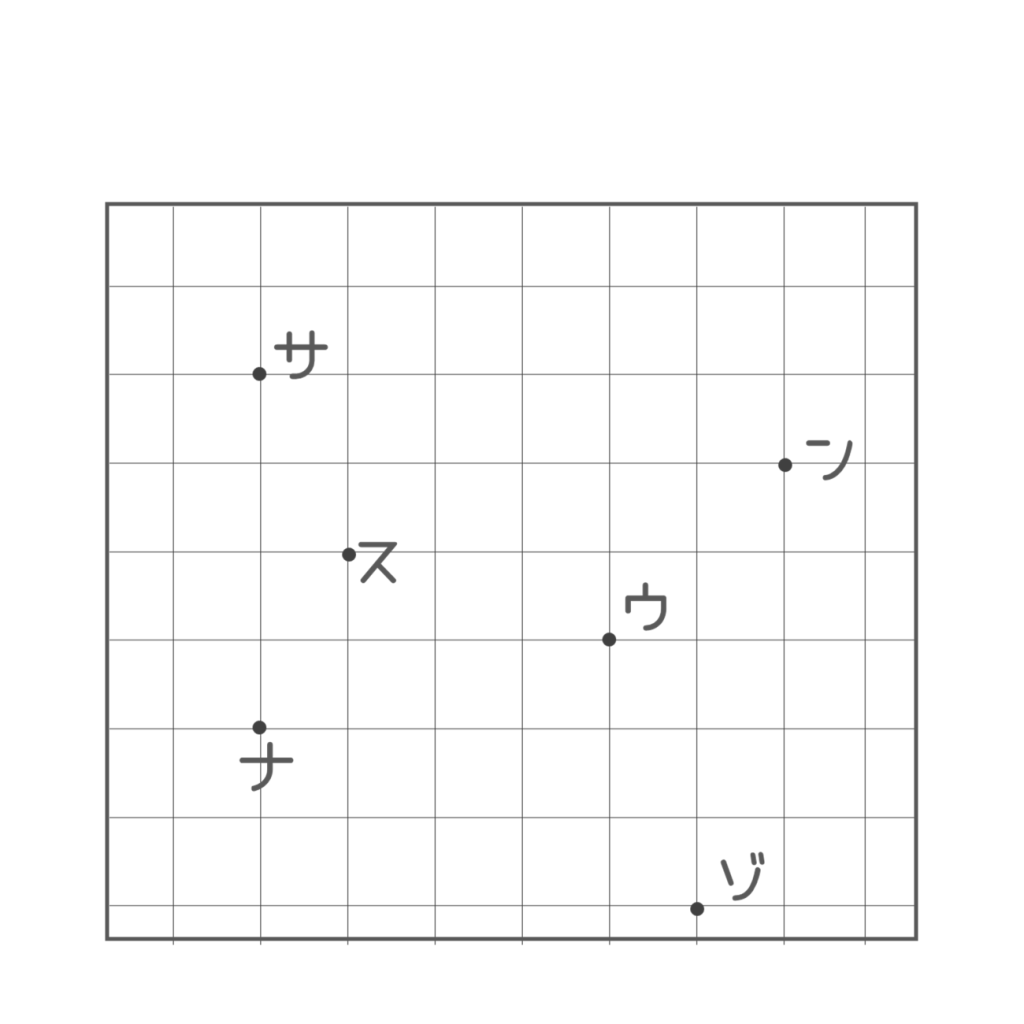
では、コンパスで円を描いていきます!
まずは、中のほうにある点を選んで、その点を中心とした半径3~5マスの円を描いてみましょう。できれば、途切れることなく完全に円が枠にはいるような半径にしてみてください。
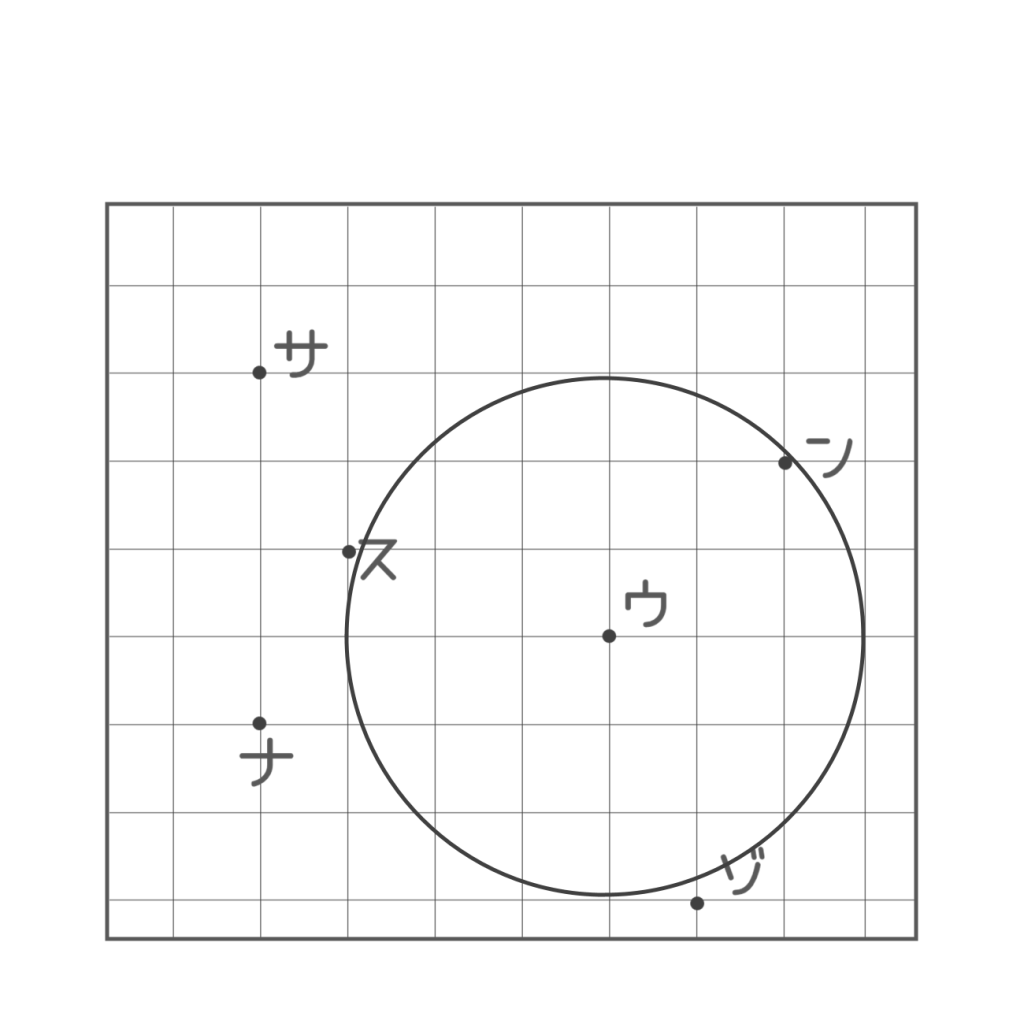
それがかけたら、他の点も同様にそこを中心とした円を描きましょう。なれてきたら半径を1・2マスや6・7マスにしてもいいかもしれません。枠からはみでた部分はかかないでおきます。ただし、1~2つは完全な円があったほうがよいと思うので、半径をうまく調節してみてくださいね。
 ずーさん
ずーさんコンパスまだなれてない!何回も消すかも……という人は、1つ円がかけるごとにペンでなぞっておいてもいいかもしれません!ファイト!
手順4
最後に、ダミーの点を打ちます。本当の中心の点のそばに1~3個点をかいて、適当に文字を入れましょう。
 ずーさん
ずーさん完成!! やったね!
せっかくだから、楽しくね!
いかがでしたか?
ナゾトキに挑戦することで、「円」や「中心」の意味を確認し、
作問することで、「さまざまな半径の円」をかく経験ができたかと思います!
今回の問題は、できた模様に色をぬっても楽しいかもしれませんね!
そしてその過程で、
どんどん「円」への理解を深めていったり、コンパスに慣れてくれたらうれしいです!
それでは、また次回の記事でお会いしましょう!
お読みいただき、

(文責:河野梓)
毎週出題しています!
ずーさんもせっせと作問中!
作った問題は私のXアカウント、もしくはLINE公式アカウントで公開しています!
今回説明した円の知識を使うナゾトキもあるので、是非、公式LINEを友達登録して「sns009」と打ち込んでみてください!答え合わせもできます!
『算数ナゾトキ20』発売中☆
また、いろんな算数ナゾトキを20問集めた問題集も販売しています。
直接書き込んで考えたい人におすすめです!