こんにちは、みうらです。
前回は、縦横が同数のマス目に数を並べ、各行(横の並び)、列(縦の並び)、さらに2つの対角線上の数の和がすべて等しくなる「魔方陣」をご紹介しました。
今回は、その同じマス目を使って、いつでもどこでも披露できる数当てマジックをご紹介します!
どの数を選んでも……
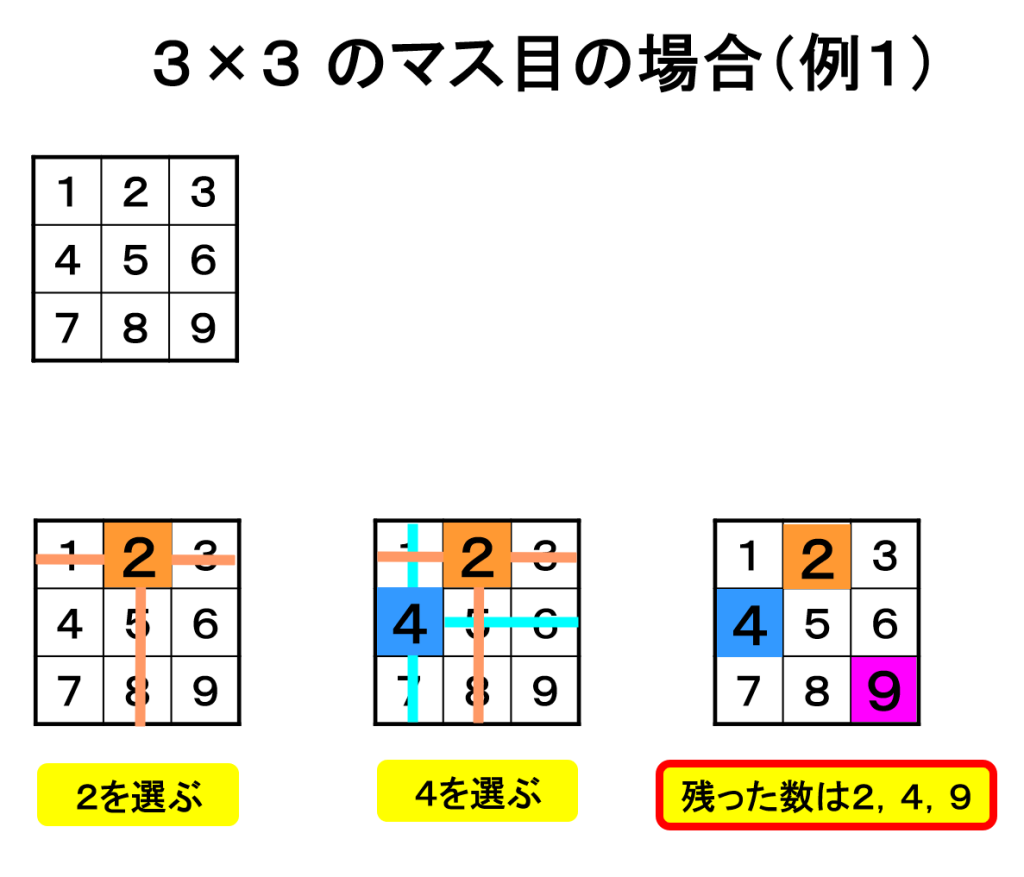
3×3のマス目を作り、左上から順に1から9までの数を書き入れます。次に、好きな数を1つ選び、その数を残して、同じ行と列にある他の数を消します。残った数の中からさらに1つ選び、同様にその行と列の数を消します。すると、3つの数が残ります。その3つの数の和を求めてみてください。

例えば、最初に「2」を選び、次に「4」を選んでみましょう。残った数は「2」「4」「9」となり、これら3つの数の和は「15」です。
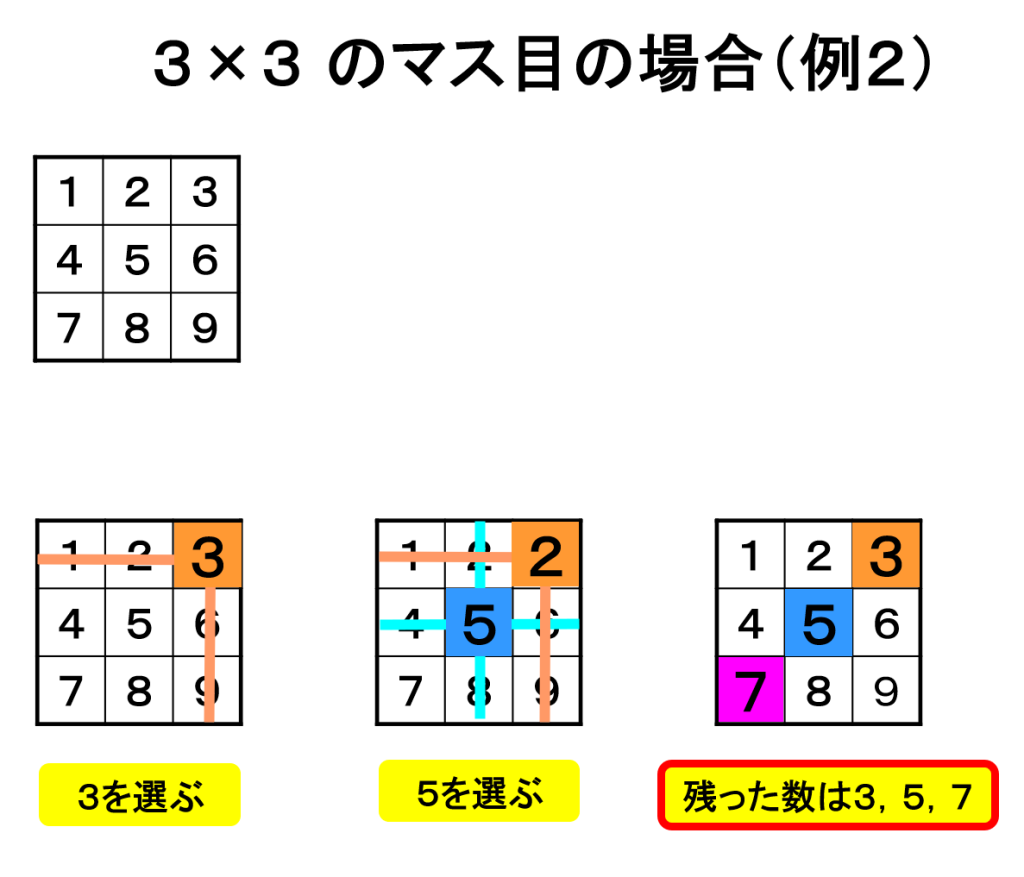
別の数を選んでみましょう。今度は最初に「3」、次に「7」を選びます。残った数は「3」「5」「7」で、その和も「15」になります。また同じ結果になりましたね。
これは偶然でしょうか?皆さんも試してみてください。やっぱり15になったでしょう。どうやら偶然ではないようです。
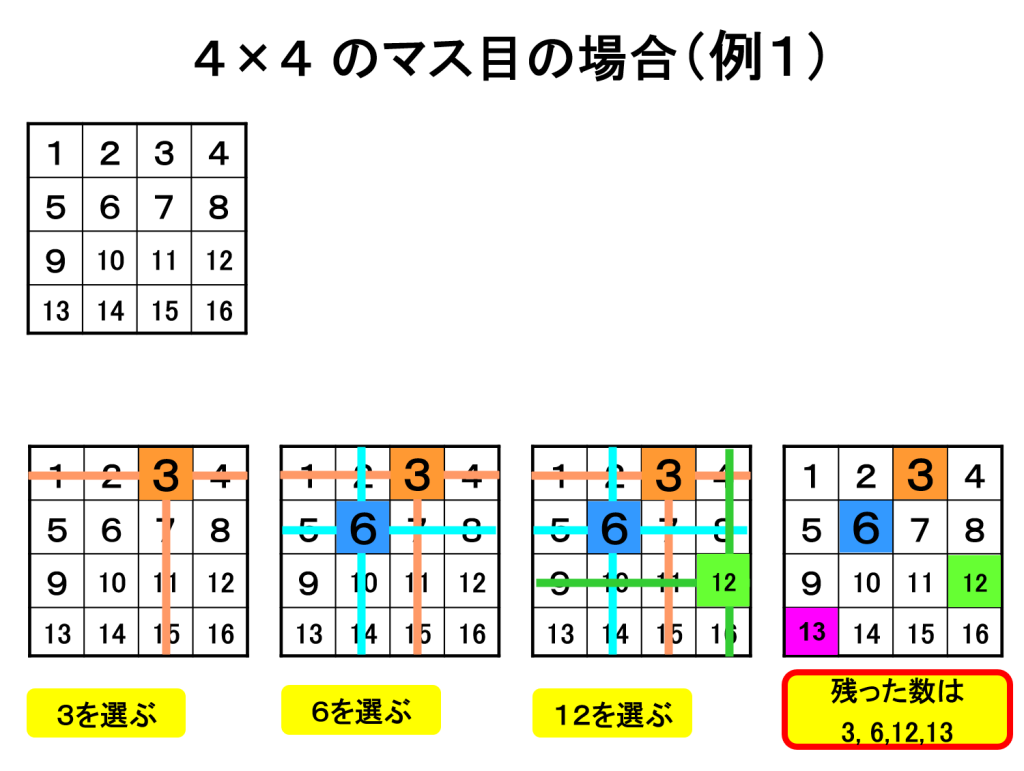
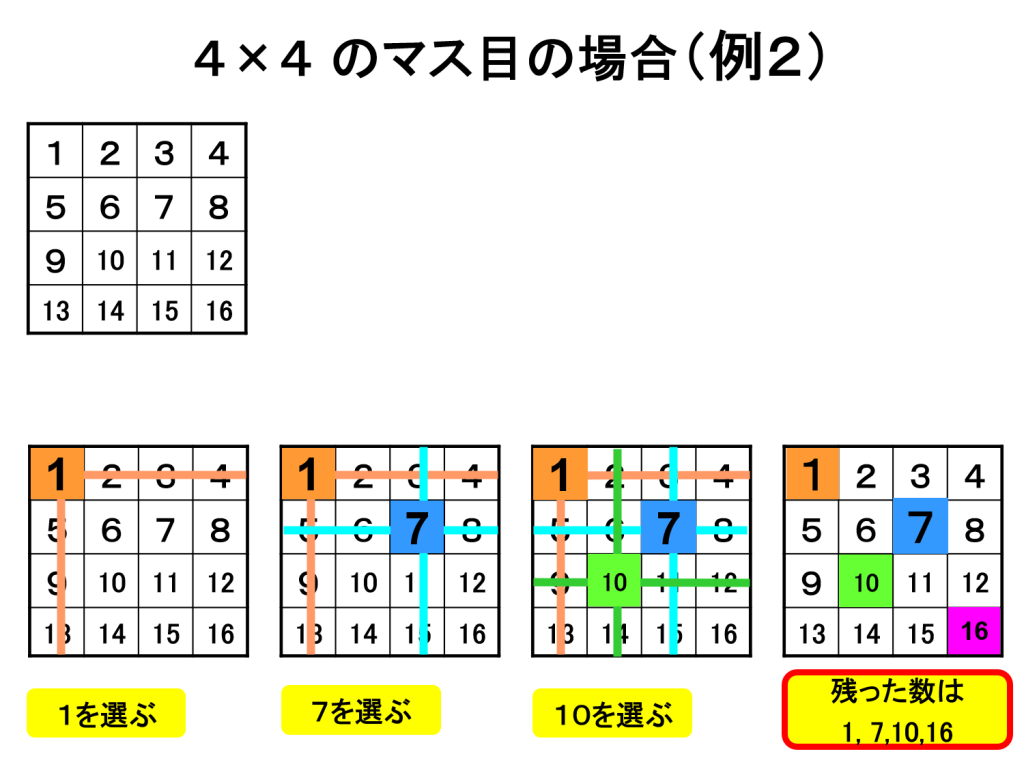
今度は、4×4のマス目で試してみましょう。4×4のマス目では、1つ数を選んで、その数を残し、同じ列と行にある数を消すという操作を3回行います。すると、残った数は4つになります。それらの数の和はいくつでしょうか?

最初に「3」を選び、次に「5」を、最後に「12」を選んでみましょう。残った数は「3」「5」「12」「13」となり、これら3つの数の和は「34」になりました。
別の数を選んでみましょう。今度は最初に「1」、次に「7」を、最後に「10」を選びます。残った数は「1」「7」「10」「16」で、その和も「34」になります。
また同じ結果になりましたね。
5×5のマス目で試してみてください。4回消す操作をして、5つの数を残すと、残った数の和は65になるはずです。
なぜこうなるの?
どうやら、このようにマス目で数を消していく操作を行うと、選んだ数にかかわらず、残った数の和が マス目のサイズに依存して 常に同じ値になるようです。
たとえば、3×3のマス目では和が15に、4×4のマス目では和が34に、5×5のマス目では65になるといった具合です。
実は、どんな消し方をしても答えは変わりません。
なぜこうなるのでしょうか?
素朴に場合を尽くしても、同じ値になることを確認できます。
つまり、3×3のマス目の場合、最初に数1を選ぶと、5, 6, 8, 9が残ります。次に5を選ぶと9が残り、6を選ぶと8が残ります。この操作を、数1から9まで全てに繰り返すと、繰り返す回数は9(最初の数の選び方)×4(最初の数を決めた際に残る数の個数)で、合計36回になります。
そして、すべての場合で残った3つの数の和が15であることが分かります。
しかし、これでは大変ですね。もっと効率的な方法を考えましょう。
マス目を左から1列目、2列目と呼ぶこととします。
そして、残った数を見て、数がどのように散らばっているかを確認します。
3×3のマス目では、残った数は1列目から3列目までの各列に1つずつ存在します。
一方、4×4のマス目では、残った数は1列目から4列目までの各列に1つずつあります。
これで勘の良い方は何かに気づいたかもしれません。下の図を見るともっとはっきりわかりますね。
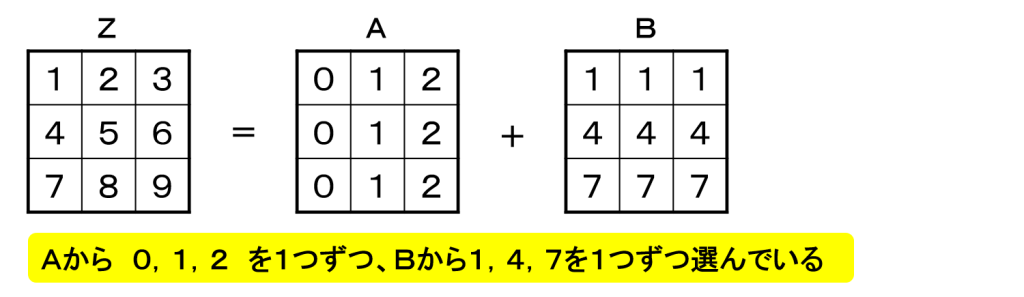
マジックで並べた 3×3マス目(Z)の数は、2つのマス目((A) (B))の数の和で表されます。
Zの各行各列から数を1つずつ選ぶと言うことは、AとBの対応する 各行各列 から1つずつ選んでいることと同じです。
つまりAから、0,1,2を1つずつ、Bから1,4,7を1つずつ選んでいることになります。
従って、 Zの各行各列から数を1つずつ 選んだ3つの数の和は、(0+1+2)+(1+4+7)=15となります。4×4のマス目の場合も同様です。
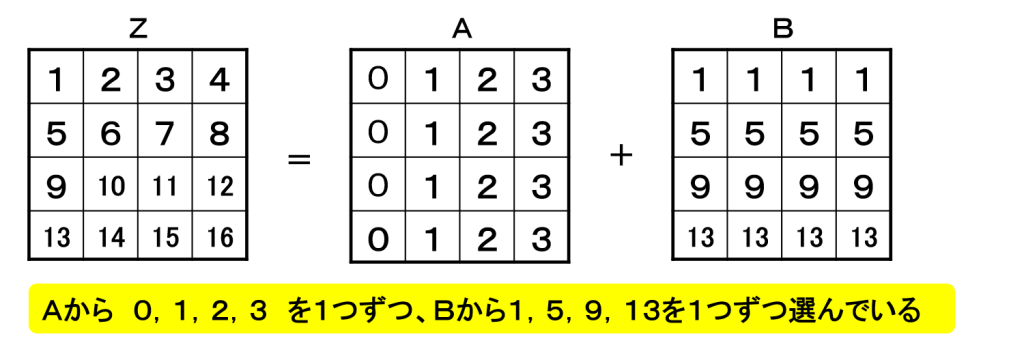
一般の場合は
一般に○×○のマス目では残った数の和は、第1列の数の和に、1と2と…(○-1)を足したものになります。
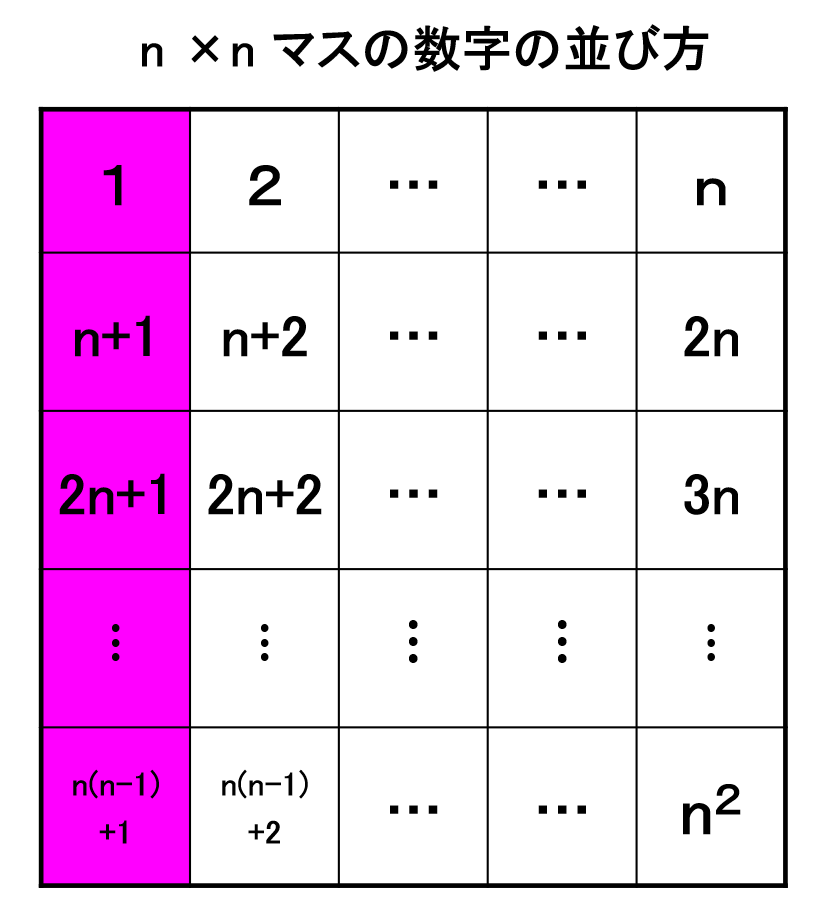
文字式や数列が分かっている皆さん向けに n×n のマス目の場合に数の和は値がどうなるか示しておきます。ここは読み飛ばしてもかまいません。
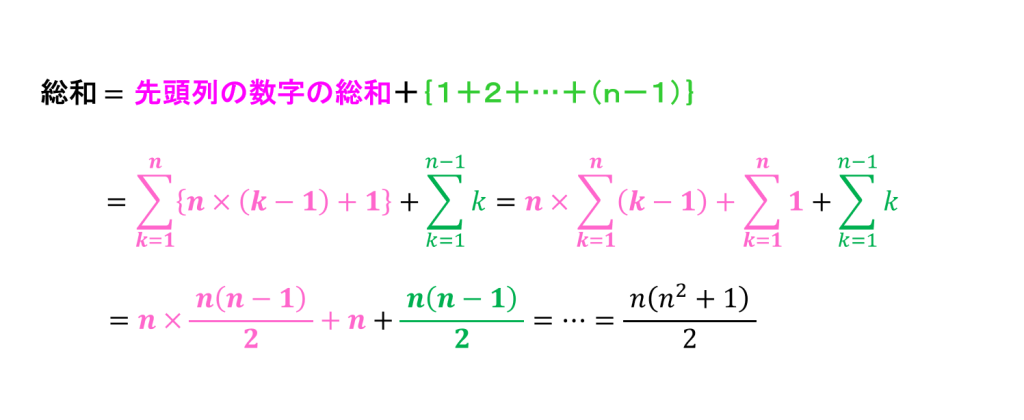
おわりに
このマジックは、どこでも簡単にできます。ぜひ周りの人に披露して驚かせてみてください。
さらに、仕組みを説明することで、あなたの知的な一面もアピールできます!
ところで、残った数の和は、3×3のマス目で15、4×4のマス目で34、5×5のマス目で65……でした。
この値、見覚えはありませんか?
実は、この数は前回ご紹介した魔方陣の縦横斜めの数の和、つまり定和と一致しています。
単に同じマス目を使っているだけではなかったのです。その理由については、ぜひ皆さんで考えてみてください。
(文責:みうら)
著者プロフィール 数学博識王みうら(三浦章)

みうら(三浦 章) math channelマガジン数学博識王
国立市在住。東京工業大学大学院修士課程を修了後、通信キャリヤで30年ほど通信サービスの研究実用化に従事。15年ほど前に、大学教員に転身。情報システム、数学、問題解決フレームワーク等を教えてきました。5年ほど前から地元公民館で月2回程度市民向け数学教室も開催しています。近頃は数学的背景のあるパズルに興味があり、その内容の発信にも関心があります。博士号(工学)、高校教員免許(数学)あり。
■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。
ぜひ、お手にとってご覧ください!