私が考える「算数の勉強のゴール」【もったいない「短期記憶」を、どうすれば「長期記憶」に移せるのか？】

こんにちは、うっつんです。 
突然ですが、皆さんは算数の勉強をどのようにしていたでしょうか。 
算数は「暗記する教科ではない」と言われながら、「解き方」や「公式」を覚えるのが算数の勉強方法だと考えている方も多いかもしれません。
そんな方はぜひ、この記事を読んでみてください。
算数に対する考え方やお子様への勉強方法のアドバイスに用いてもらえるように、今回の記事では算数の勉強でもったいない短期記憶のみの学習と最終ゴールである長期記憶について話していきます。 

短期記憶と長期記憶 

まず、記憶には大きく分けて2種類の記憶があります。
2つについての詳しい話はできませんが、ざっくりいうと「忘れてもいいように覚えた短期記憶」と「忘れにくい記憶である長期記憶」だとこの記事では解釈してください。 

長期記憶しているものとしては、箸の持ち方、衣服の脱ぎ方などです。
これらは生活をしていて「やり方を忘れた！」と困ることはないと思います。
なぜなら、習慣化していて脳に定着しているからです。 

一方で、短期記憶になりやすいものとしては行政手続きや着物の着方などです。
これらは仕事などで日常的に使う人以外は日常生活で使う回数が限られたいるため、必要なときに調べてしばらくすると忘れてしまうことが多いのでないでしょうか。
そして、また必要なときに調べるということを繰り返す経験がみなさんあるのではないでしょうか。 

勉強において「暗記をする」というのは、この2つのうち短期記憶のことをこの記事では指します。
学生時代の勉強において暗記するものの代表例としては、理科や社会で習う単語があります。これらは社会人になって思い出すのが難しいことが多いです。
一方で、長期記憶しているものもあり、その例が漢字です。
習った全ての漢字を覚えているのは難しいですが、自分の名前の漢字などは社会人になっても書けなくなることは少ないはずです。 

算数の学習のゴールは長期記憶 

それでは算数の学習のゴールについて考えていきます。
私が考える学習のゴールを、九九の学習を使って説明していきます。

九九では、学習を始めた際には「いんいちがいち、いんにがに、……、くくはちじゅういち」と語呂合わせを唱えて覚える子が多いと思います。
このとき、発声することで口や耳でも覚えることで短期記憶がしやすくなります。
そうして短期記憶した九九は、かけ算を解くときに、次のステップでアウトプットされると考えています。 

繰り返しかけ算の練習をしていくと、３つのステップをほぼ同時にできるようになります。
（多くの人はこのアウトプットが当たり前になっているので、3ステップになっていることに気づかないかもしれません）
こうなると長期記憶に保存されていくと考えています。
長期記憶になってからも練習をさらに繰り返すことで、アウトプットがはやくなり計算速度も上がっていきます。 

こうして長期記憶になった九九は忘れづらく、テストの度に勉強しなおすことは少ないはずです。
そのため、かけ算qは算数の色々な単元に登場し九九を必ず使いますが、あまり苦労せず九九を思い出せていると思います。
特に、算数の得意な子は反射的に九九の答えが出てきています。

私が考える算数のゴールは、このように長期記憶に単元の理解が移り、別の単元の学習で再度出てきたときに勉強しなおすことがないような状態です。

もったいない学習

それでは逆にもったいない算数の勉強方法とはなんでしょうか。
速さの単元を例にそのもったいなさを説明します。

速さでは、「きはじ（みはじ）図」というビジュアルを使って速さの3公式を覚えるやり方があります。
この方法では、距離（道のり）、速さ、時間の頭文字と横に並んでるのはかけ算、上下に並んでるものは割り算（上÷下）として3公式を覚えます。 

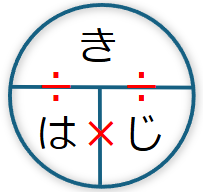
この方法で速さの問題を解くステップは、例えば次のように考えられます。 

繰り返しきはじ図を書いて、公式を思い出すことで長期記憶にすることは可能ですが、九九よりも難易度が高い上に速さの問題は解けるようにはなりません。
理由は２つの目のステップがきはじ図の暗記のみではできないことだからです。
そのため、長期記憶には移ることなく、短期記憶で終わってしまうでしょう。算数で速さの学習をした後しばらくすると忘れてしまい、中学校の数学で算数の復習や方程式の文章題で再度覚えなおすという負担が発生します。
その負担がかかる分だけ新しい学習に時間をかけれず、以前の学習に時間がかかってしまうことが多いのがとてももったいないです。

これを改善するためには、距離、速さ、時間の意味をしっかり理解することが必要です。
実は、それができれば、速さの公式は覚える必要がありません。
例えば、距離は「ある時間をある速さで進んだ長さ」なので「時間×速さ」が自然と出てきます。
この方法で速さの問題を解くステップは次のようになると考えています。 

この方法で速さの問題を繰り返し解いていくと、最初の３つのステップがほぼ同時にできるようになります。
こうすることで速さの公式だけを覚えようとするよりも、言葉の意味を理解して計算式を考える方が記憶に残りやすくなるうえに解くスピードも速くなることが多いです。

継続することを大事にしよう

今回話した算数の学習方法について一番重要なポイントは継続することです。
九九のように繰り返すことで長期記憶に移るという点に加えて、継続することて必ず成果が見えるタイミングがあります。
成果が見えるようになると学習が楽しくなったり、もっと成果を出したくなったりと、継続すること自体が苦ではなくなります。

そこまで諦めずに続けるために、短期的な目標設定だけではなく1年後などの長期的な目標をお子様と一緒に決めたり、精神的にくじけそうになった時に自己肯定感を高めるサポートしたりすることも効果的です。
算数の勉強は、一つできないままにしておくと後々とりかえすのが難しくなります。
一つ一つの単元を長期記憶に移るまで学習を続けることで、算数への苦手意識が芽生えるお子様が少なくなることを願っています。

（文責：宇都木一輝）