こんにちは。中学受験算数ナビゲーターの滝澤です。
今回のテーマは、「設問の前に考えよう」です。
桜蔭中学の変わった時計の問題を取り上げます。
問題です。/桜蔭中学(2019年、問題4)
2019年 桜蔭中学 第4問「変わった時計」
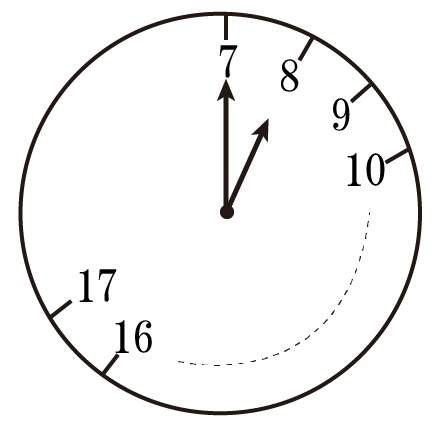
図のようなかわった時計があります。この時計には,7から17までの数字と目盛りが書いてあります。7と8,8と9,9と10,……,16と17の目盛りの間隔は,すべて等しいとします。午前7時を8時0分,午後1時を13時0分のように表すことにします。8時0分のとき,右の図のように時計の長針は7,短針は8を指します。長針と短針は右回りになめらかに動きます。長針は次の①②の規則に従って動きます。
① 長針は7時0分から17時0分までは60分で1周します。
このとき,長針と短針はそれぞれ一定の速さで動きます。
② 長針は17時0分から7時0分までは168分で1周します。
このとき,長針と短針はそれぞれ一定の速さで動きます。
長針が1周する間に短針が回転する角度は,①のときも②のときも同じで,短針は24時間で1周します。ただし,普通の時計と同じように1時間は60分です。
(1) 次の( ア )と( イ )にあてはまる数を答えなさい。
長針が1周する間に短針が回転する角度は ( ア )°で 時刻が12時45分のときの長針と短針がつくる角の大きさは( イ )°です。ただし,長針と短針のつくる角の大きさは0°以上180°以下とします。
(2) 10時0分から11時0分の1時間で,長針と短針のつくる角の大きさが60°になる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
(3) 17時0分から翌日の7時0分の間で長針と短針が重なる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
まずは設問の前に,一旦考えましょう。
中学受験算数でいう、時計算というジャンルの問題ですね。
ふつうの時計であれば、短針と長針があります。長針は60分で1周、短針は12時間=720分で1周しますね。つまり長針は1分間に6°、短針は1分間に0.5°動くわけです。
これを利用して、短針と長針が重なる時刻やある角度になる時刻、または、ある時刻における短針と長針のなす角度を求めたりするのが、時計算の基本的な問題です。塾などでは小5の秋から冬に学習すると思われます。
さて、この時計の特徴を考えましょう。
どうやらこの時計は、1日のうちに2通りの動き方をするようですね。時計算の基本は、短針と長針の動くスピードです。まずは長針が1周する時間を考えましょう。
「168」ってなんだ?
ここで実は「168ってなんだ?」と考えることが大切です。
168は2×2×2×3×7ですね。
17時0分から7時0分までは14時間ですから、「ははあ、なるほど計算しやすい数にしているな」と考えるわけです。
① 7時0分から17時0分までは、長針は60分間で1周しますね。10時間で10周します。
② 17時0分から7時0分までは、長針は168分間で1周しますね。14時間で5周します。
次は短針です。「長針が1周する間に短針が回転する角度は、①のときも②のときも同じ」ということは、
① 7時0分から17時0分までは、「長針が1周する間に短針が回転する角度」の10倍、短針は動く。
② 17時0分から7時0分までは、「長針が1周する間に短針が回転する角度」の5倍、短針は動く。
ということになりますので、文字盤の7から17までの角度は、17から7までの角度の2倍となり、合計360°ですから、文字盤の7から17までは240°よって数字と数字の間は24度、そして17から7までは120°とわかるわけですね。なるほど時計の絵でも大体そのくらいの角度になっているなと確認して、では設問を見てみましょう。
それでは1問1問説明していきましょう
(1) 次の( ア )と( イ )にあてはまる数を答えなさい。
長針が1周する間に短針が回転する角度は ( ア )°で 時刻が12時45分のときの長針と短針がつくる角の大きさは( イ )°です。ただし、長針と短針のつくる角の大きさは0°以上180°以下とします。
実は時計算で聞かれる一般的な問題です。
アは1つの数字分動きますから「24°」とわかります。イは長針と短針が1分間に何°動くかを考えます。
長針は360÷60=6°/分、短針は24÷60=0.4°/分ですね。
12時0分では長針と短針のつくる角は24×(12-7)=120°で、45分間で長針の方が短針よりも5.6×45=252°多く進むので、12時45分のときの長針と短針のつくる角は、 252-120=132°となります。
(2) 10時0分から11時0分の1時間で、長針と短針のつくる角の大きさが60°になる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
これも時計算の基本的な問題ですね。同じように考えていきましょう。
10時0分のとき、針と短針のつくる角は72°ですね。長針と短針のつくる角の大きさが 60°になるのは、72°から12°縮まったとき(長針が短針より12°多く進むとき)と、72°が縮まっていって0°になって長針が短針に重なり、さらに60°開いたとき(長針が短針よりも60+72=132°多く進んだとき)の2回です。
よって、「12÷(6-0.4)=2と$\frac{1}{7}$分」と「132÷(6-0.4)=23と$\frac{4}{7}$分」となります。
(3) 17時0分から翌日の7時0分の間で長針と短針が重なる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
「長針と短針が重なる時刻」も時計算としてはオーソドックスなテーマです。考え方は同じですね。
まず、17時~7時の長針と短針の1分間の速さを考えましょう。
長針は168分間で360°ですから1分間に2と$\frac{1}{7}$°、短針は168分間に24°なので1分間に、$\frac{1}{7}$ °進みます。ということは、1分間にちょうど2°ずつ角度が縮まっていくのですね。
17時0分のとき、長針と短針のつくる角は240°なので、はじめに長針と短針が重なるのは、「240÷2=120分後」の19時0分。
長針と短針が重なってから次に長針と短針が重なるまでに、長針は短針よりも360°多く進むので、「360÷2=180分後」ごとに重なることになります。
つまり、19時0分、22時0分、1時0分、4時0分、7時0分ということです。
想像力って楽しいですよね。
いかがだったでしょうか。今回は少し高学年向きの内容になってしまったかもしれません。
けれども時計は生活の中で慣れ親しんだ題材ですので、それをこんなふうに想像して変わった時計を考えてみるのは面白くないですか?
このような設定を面白いと思えたら、素敵ですよね。
こんな複雑な動き方をする時計でも重なる時間は実はちょうど0分になるように作られているのですね。
難しそうに思えますが、この時計の長針と短針の動き方や、文字盤の配置(数字と数字が何度はなれているかなど)を設問に答える前に考えておけば、基本問題と解き方は同じです。
設問を見てしまうと、その問題のことだけを考えてしまいがちです。
ですから聞かれたことを考えるより前に、聞かれてはいないけれども自分で疑問点を見つけて、先回りして計算してしまうことが必要なのです。
それにしても17時から7時までは時計としては使いづらい時計ですね。7時から17時までは使えそうなので、例えば学校などではいいのかもしれません。
さて次回ですが、ふだんの生活でも見ることのある図形の問題です。ちょっとだけお見せしましょう。
次回は、灘中学から「見たことのある図形」についての出題です。
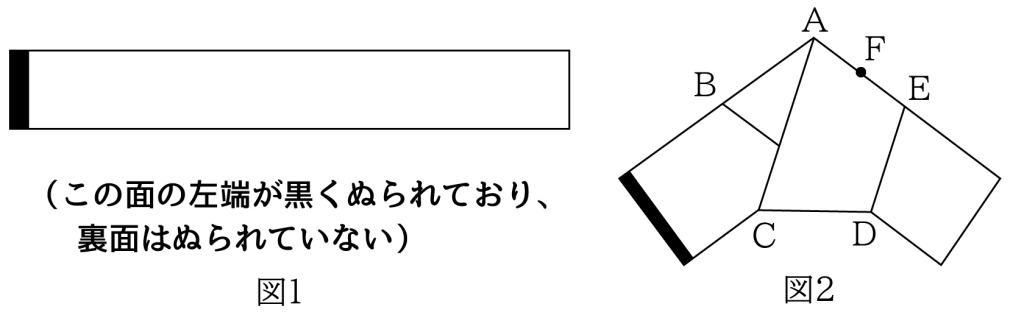
図1のような長方形の細長い紙を3つの折り目で折り込み、図2のようにしました。5個の点A、B、C、D、Eを頂点にする五角形は正五角形です。また、点FはAEの真ん中の点です。
この題材でどんな問題が出題されるのか、楽しみにしていてください。









