こんにちは、math channelマガジン編集部です。
素数を見つけるためにはいくつかの方法があります。
今回はその中の1つである「エラトステネスの篩(ふるい)」について紹介します。
エラトステネスの篩とは、「素数の約数は1と自分自身の2つのみ」という性質を利用して素数を見つける方法です。今回は1~100までの数から素数を見つけましょう。
- まずは1を消す
- 2の倍数を消す
- 3の倍数を消す
- 5の倍数を消す
- 7の倍数を消す
- 残った数が1~100までの素数
まずは1を消す
最初に1を消します。
次に、2は素数ですので「〇」を書きます。一方、2の倍数は約数に必ず2が入ってしまうので素数ではありません。ですので2より大きい2の倍数を消していきます。

これで、2の倍数以外の数が残りました。
同じように3の倍数も消してみよう
消されずに残っているマスのうち、一番小さい数は3です。
同様に3の倍数も消してみると……

だんだん残っている数が少なくなってきましたね。
消されていないマスの中で一番小さい数は5になので、また同じように5の倍数も消してみます。
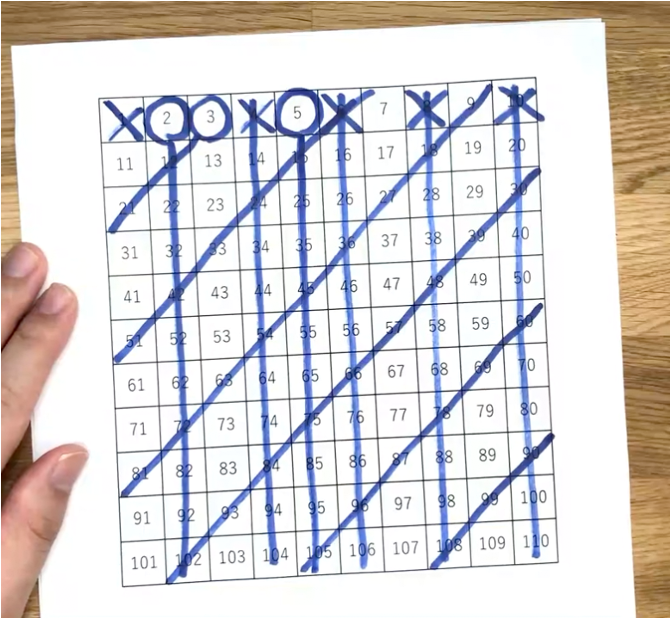
消されてていない数を見ると、九九表にはない数が多くなってきました。
次に7の倍数を消していきます。
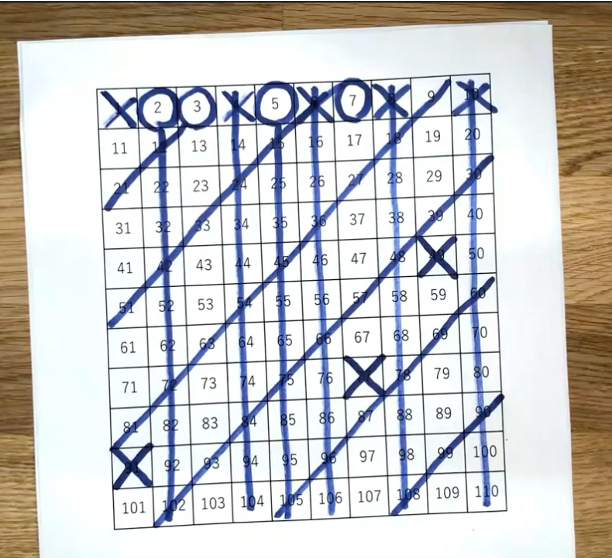
7までくると、新たに消すところは3か所のみ。だいぶ少なくなりましたね。
ここまで来てでも消されず残った数が、1~100までの中にある素数となります!
実は7まで調べると、この方法では120までの素数を探し出すことができます。
(11まで調べると168まで素数を探し出すことができます)
エラトステネスの篩、あなたもやってみませんか?

エラトステネスの篩、いかがでしたでしょうか?
単に素数を丸暗記するのではなく、九九表に表して見つけ出すと視覚的にも分かりやすいですね!
やってみたいという方は、ぜひ写真で使っているシートをダウンロードして試してみてください。
算数の「面白さ」「楽しさ」に出会えるmath channelの講座
math channelでは、算数・数学の「面白さ」「楽しさ」に出会える様々な講座を用意しています。
「わかった!」「なるほど!」「面白い!」が詰まったmath channelの講座で、算数・数学への新しい扉を開いてみませんか?
小学生におすすめの2つの講座
今すぐ申し込み可能な全講座
今すぐにお申し込みいただける講座は、以下のリンク先よりご確認いただけます。
出張講座のご依頼も承ります
数学のお兄さん・横山明日希やmath channel編集長のぬまちゃん、算数のお兄さん・よしだしんや、中学受験算数ナビゲーター・滝澤幹、数学博識王みうら、算数ナゾトキのずーさんなど、算数・数学を楽しさを伝える伝道師であるmath channelメンバーによる出張講座を開催しませんか?
全国どこでも出前講座の開催が可能です。
また、オンラインでも開催できます。
まずはお気軽にご相談ください。
詳しくは下記リンク先をご覧ください!

■math channelマガジン編集部の本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。
ぜひ、お手にとってご覧ください!














