三角形の“心”にせまる【その1】～ チェバの定理から見えてくる“重心”の不思議〜

三角形には、見た目以上にたくさんの不思議が隠れています。
その中でも、三角形の特別な「心（しん）」と呼ばれる点──重心・垂心・内心・外心──には、みんなの興味をひく性質があります。

それは、「三角形の3つの頂点と辺の特別な点を結ぶ直線が、ぴったり1か所で交わる」という不思議な性質、つまり「共点性（きょうてんせい）」と呼ばれるものです。

この現象は単なる偶然ではなく、とても美しい「チェバの定理」を使うと、きちんと説明できます。

ただし、チェバの定理を使いこなすためには、三角形の基本的な性質（たとえば、三角形の相似の条件や、円の外側から引いた2本の接線の性質など）を少し知っていると理解がスムーズです。

でも心配いりません。これらの知識は中学生でも十分に学べる内容で、難しすぎるものではありません。

ちなみに、三角形には “傍心” というちょっと変わった「心」もありますが、これはチェバの定理の少し複雑なバージョン（外角を使う場合）に関係するため、今回のシリーズでは扱わないことにしました。気になる方は、ぜひ自分で調べてみてくださいね。

この連載の第1回では、まず「心」について軽く紹介し、その後にチェバの定理を解説します。
そして、最も基本である「重心」がなぜ共点になるのか、その秘密をわかりやすく紐解いていきます。

垂心・内心・外心については、次回以降に順を追って解説しますので、安心して読み進めてくださいね。

三角形の“心”とは

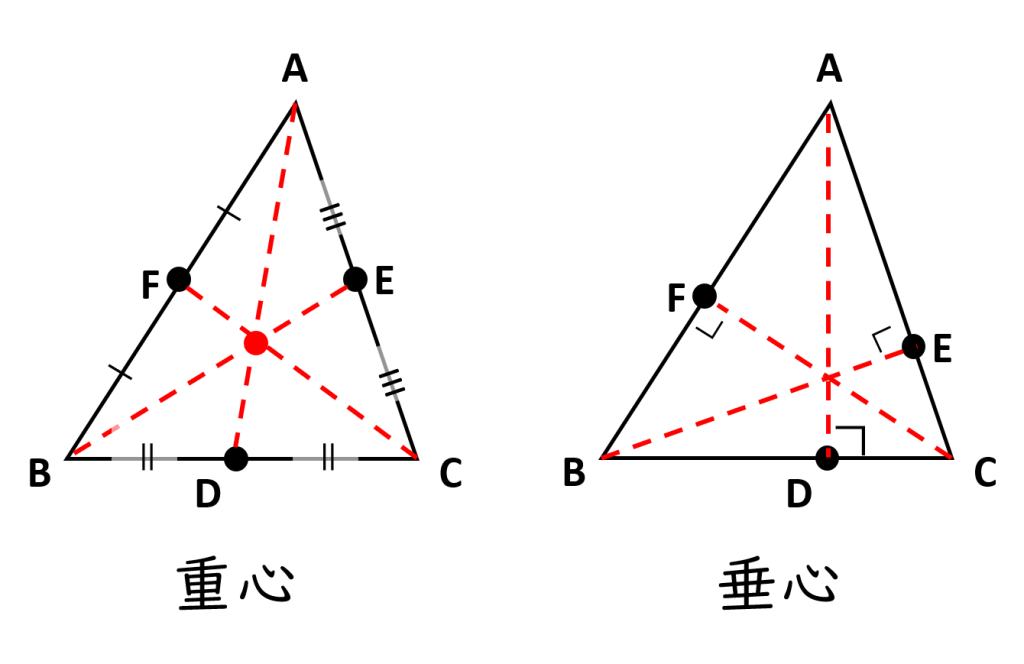
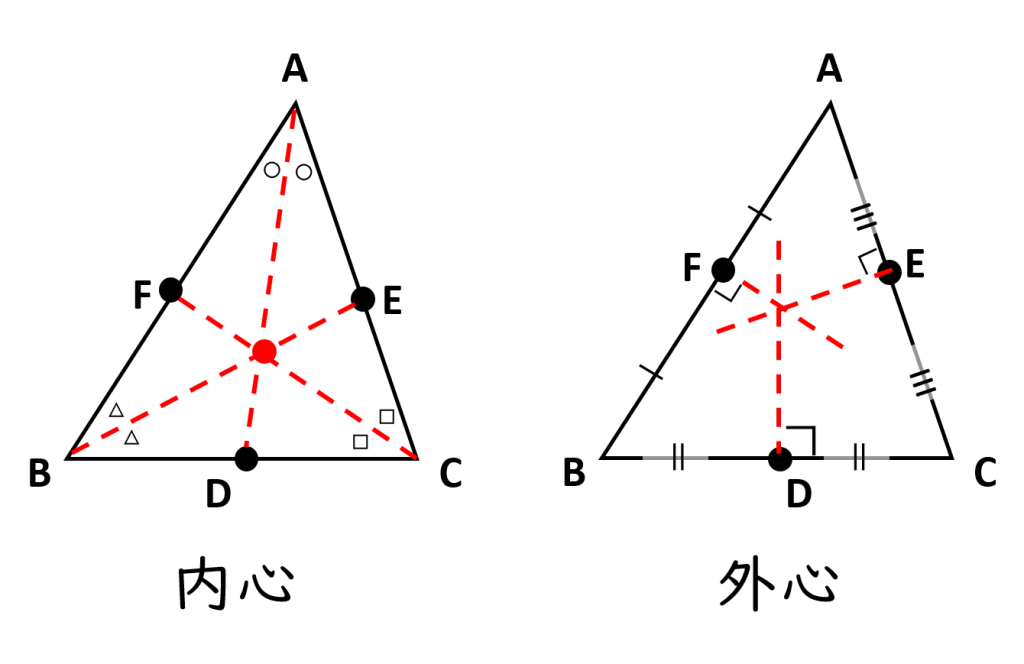
「重心・垂心・内心・外心」とは、下の表にまとめた三角形における特別な交点です。

いずれの心も3本の直線が1点で交わっています。不思議ですよね。

チェバの定理とは？

三角形の「3本の線が1点に交わる」という現象を説明する最大の武器が「チェバの定理」です。

この名前は、17世紀イタリアの数学者 ジョヴァンニ・チェバ（Giovanni Ceva, 1647–1734） に由来します。
ミラノ出身のチェバは、三角形の構造に深い関心を持ち、この共点性に関する定理を 1678年ごろ に発表しました。

彼は数学だけでなく、力学や水理学にも造詣が深い多才な人物で、幾何学を使って構造物の安定性を分析するなど、実践的な研究にも取り組んでいました。
このような応用的な視点が、「3本の線が1点で交わるための条件」という発想を導いたのかもしれません。

さて、そのチェバの定理とは、三角形において、頂点から対辺に引いた3本の線分が1点で交わるための条件を、「辺上の点と頂点間の長さの比の積」で示すものです。

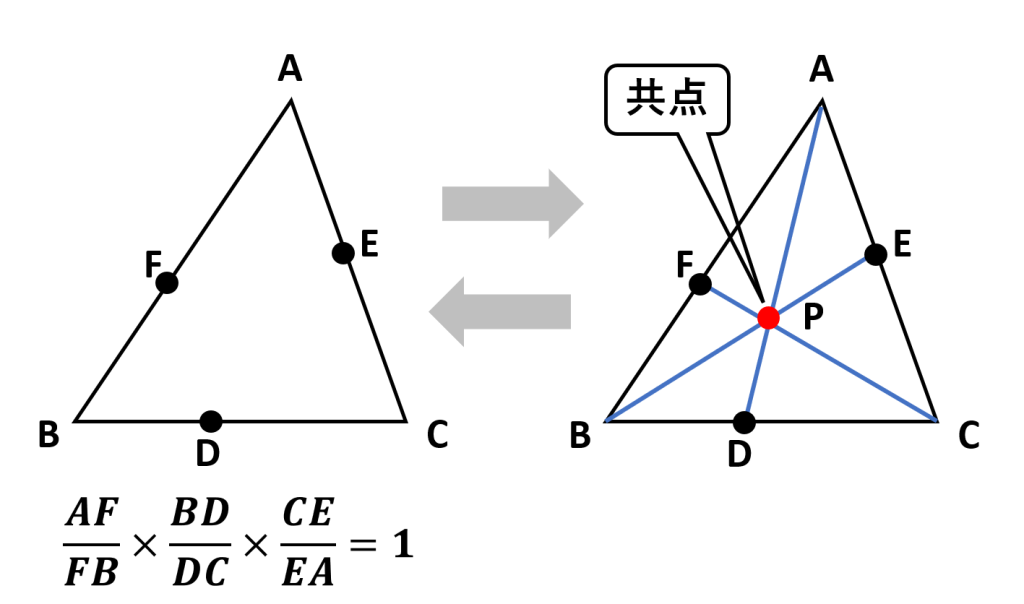
定理

三角形ABCと１点Pがあるとき、AP, BP, CPがBC, CA, ABと交わる交点をD, E, Fとすれば、

$$\frac{AF}{FB} \times \frac{BD}{DC} \times \frac{CE}{EA} = 1 \quad \cdots\;※$$

が成り立つ。

定理の逆

三角形ABCの辺BC上に点Dを、辺CA上に点Eを、辺AB上に点Fをとる。
このとき、※が成り立つならば、3直線AD, BE, CFは1点で交わる。

まずは「重心」から ― 最も基本の共点性

チェバの定理を使うと、「重心」の共点性を説明することができます。

三角形ABCにおいて、それぞれの辺の中点を以下のように定めます：

• 辺BCの中点 → D
• 辺CAの中点 → E
• 辺ABの中点 → F

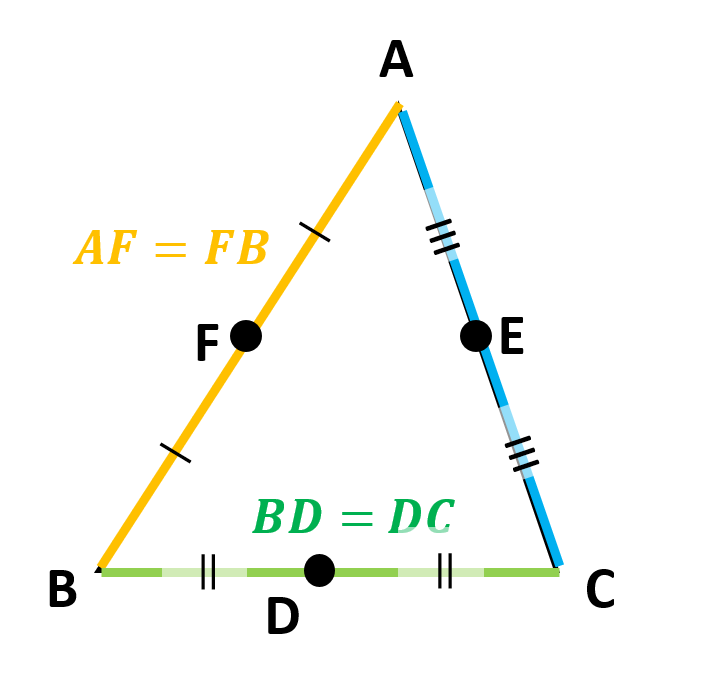
このとき、BD = DC、CE = EA、AF = FB より

$$\frac{AF}{FB} \times \frac{BD}{DC} \times \frac{CE}{EA}= \frac{1}{1} \times \frac{1}{1} \times\frac{1}{1} = 1$$

よって、3直線AD・BE・CFは1点で交わります。

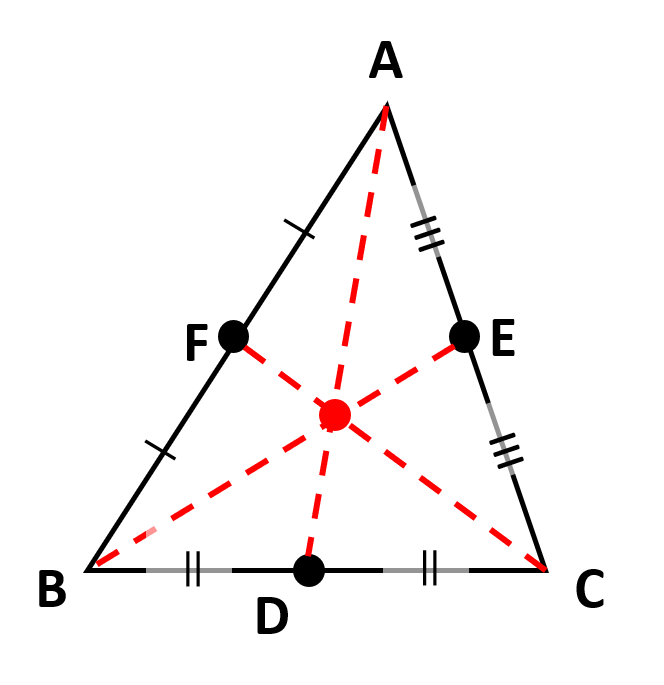
これが「重心」と呼ばれる点です。重心は、三角形の内部で、「質量の中心」や「バランスのとれた点」としても知られています。
チェバの定理の中でも、比がすべて1になる最も基本的な例として、導入にぴったりの存在です。

重心の共点性はチェバの定理を使わず、中点連結定理によっても証明できます。こちらの方法のほうがよく知られているかもしれません。
重心以外の心についても、基本的な図形の性質を使った証明は可能ですが、辺を分割する比が複雑になる場合でも、チェバの定理を使うと論理が格段に簡潔になり、より一般的な証明ができます。
チェバの定理は単に特定の点の存在を示すだけでなく、三角形の共点性を調べるうえで強力な道具です。

その2へつづく

次回の「その2」では、垂心・内心・外心というやや複雑な共点について、それぞれの定義と構造を踏まえながら、チェバの定理を用いて解説します。お楽しみに。

（文責：みうら）

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

文系オトナですが、今から数学を楽しめますか？ [ math channel ] 価格：1,760円（税込、送料無料) (2025/7/3時点) 楽天で購入

数学博識王みうらの人気記事　こちらもどうぞ！