こんにちは、うっつんです。
前回は、私の好きなパズルを通して「ひらめき」を体験する方法をお伝えしました。
「ひらめき」についてもっと体験してもらうために、今回は算数・数学の問題でひらめきを体験してもらおうと思います。
取り扱う問題は2020年の早稲田大学高等学院の入試問題です。
高校入試の問題からですが、難しい知識や計算は必要ないのでぜひ最後まで読んでみてください。
問題はこちら!
1 辺の長さが 1 の正方形 12 個によって区画された通路を、図 1 のように道路を線で表し、交差点を点として表す。地点Aから地点Bまで行くとき、次の問いに答えよ。ただし、同じ道を二度は通らないものとし、一度地点Bに到達したら、それ以降は動かないものとする。
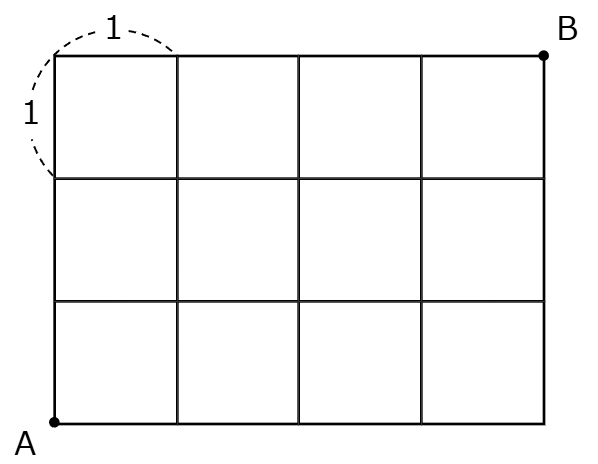
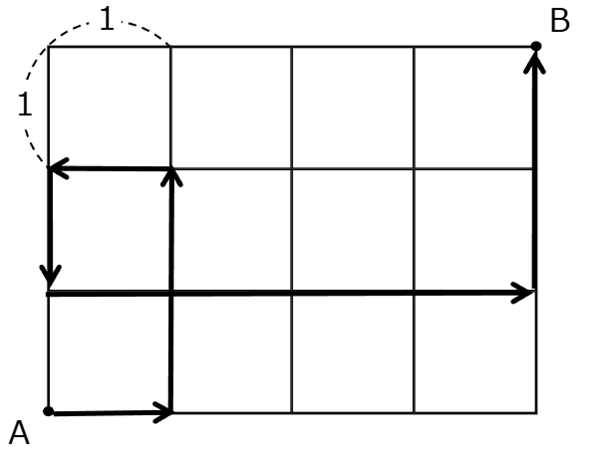
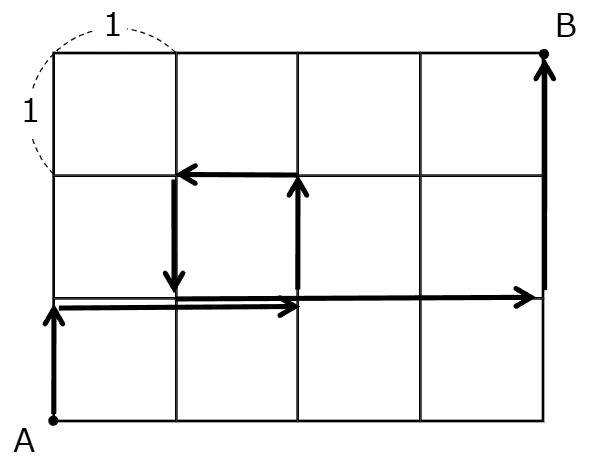
図 2 は地点Aから地点Bまでの移動距離が 11 の例である。図 3 は同じ道を二度通っている例である。
(1) 地点Aから地点Bまでの移動距離が 7 である行き方は何通りあるか。
(2) 地点Aから地点Bまでの移動距離が 9 である行き方は何通りあるか。
(3) 地点Aから地点Bまでの移動距離が 12 である行き方は何通りあるか。
(4) 地点Aから地点Bまでの移動距離として表せる数はいくつあるか。
さて、みなさんは問題をどのように読み、どんなことを考えましたか。
色々な読み方や考え方がありますが、前述のように、私が考える「ひらめき」を体験しやすい方法をご紹介します。
問いを見る前に分かることをまとめよう!
図3のように同じ場所を2度通るのは禁止なことが分かります。
また、移動距離が11の場合はAからBに行くために図2も3も一つの四角をぐるっと回っています。これについて少し考えてみましょう。
もしあなたがAからBに行くとき、同じ場所をぐるっと回っているときはどんなときでしょうか。
おそらく迷っているときや、時間に余裕がありちょっと寄り道をするときではないでしょうか。
つまり、移動距離が11のときは遠回りをしているのです。
では、遠回りをしないとどうなるのでしょうか。
それぞれの問いを見る前にこのように分かることをまとめ、そこから疑問に思ったことを整理してみてください。
また、パズルで「ひらめき」を体験してもらったときに次の3つを紹介しました。
- とにかく試す
- 自分のできることを探す
- 解けなくなったら視点を変えてみる
問題を解くときもこの3つを意識して解いてみましょう。
次からは実際に問題を解いてみましょう。
(1)の解説
先ほど遠回りをせずにAからBまで行ったらどうなるだろうと疑問が出てきましたがそれについて考えてみます。
例えば、下の2つがあります。
この移動距離を見てみると今回の問題の7になっています。移動距離が7のものがいくつかでてきたので、これについて詳しく見ていきます。
移動距離1進む事に矢印を書いて、これを順番通りに並べたものを考えてみます。
例えば、↑→→↑↑→→は下のようなルートに対応しています。
こうすることで移動距離が7のものは↑が3つ、→が4つあると分かります。
これの並び替えを考えてみましょう。
これをすべて書き出して見ると35通りになります。
ちなみに、計算でも求めることができ中学受験や高校受験では「7個の中から3つのものを選ぶ」という問題と同じやり方で$\dfrac{7\times 6\times 5}{3\times 2\times 1} =35$と計算することができます。
| ① | →→→→↑↑↑ | ⑪ | →↑→→→↑↑ | ㉑ | ↑→→→→↑↑ | ㉛ | ↑↑→→→→↑ |
| ② | →→→↑→↑↑ | ⑫ | →↑→→↑→↑ | ㉒ | ↑→→→↑→↑ | ㉜ | ↑↑→→→↑→ |
| ③ | →→→↑↑→↑ | ⑬ | →↑→→↑↑→ | ㉓ | ↑→→→↑↑→ | ㉝ | ↑↑→→↑→→ |
| ④ | →→→↑↑↑→ | ⑭ | →↑→↑→→↑ | ㉔ | ↑→→↑→→↑ | ㉞ | ↑↑→↑→→→ |
| ⑤ | →→↑→→↑↑ | ⑮ | →↑→↑→↑→ | ㉕ | ↑→→↑→↑→ | ㉟ | ↑↑↑→→→→ |
| ⑥ | →→↑→↑→↑ | ⑯ | →↑→↑↑→→ | ㉖ | ↑→→↑↑→→ | | |
| ⑦ | →→↑→↑↑→ | ⑰ | →↑↑→→→↑ | ㉗ | ↑→↑→→→↑ | | |
| ⑧ | →→↑↑→→↑ | ⑱ | →↑↑→→↑→ | ㉘ | ↑→↑→→↑→ | | |
| ⑨ | →→↑↑→↑→ | ⑲ | →↑↑→↑→→ | ㉙ | ↑→↑→↑→→ | | |
| ⑩ | →→↑↑↑→→ | ⑳ | →↑↑↑→→→ | ㉚ | ↑→↑↑→→→ | | |
(2)の解説
つぎに、移動距離が9のものを考えてみましょう。
(1) のときと比べて矢印が2つ(↓と↑) が増えています。
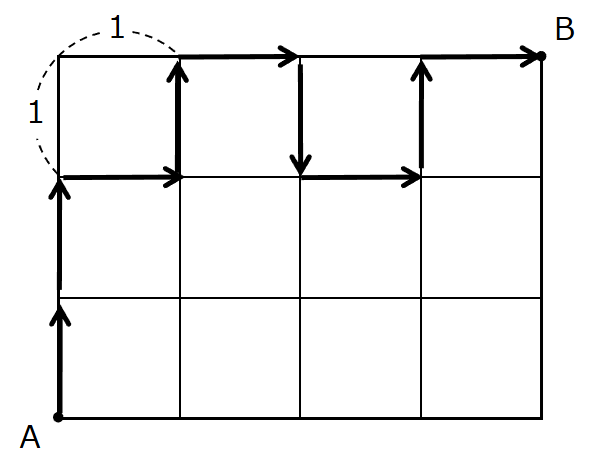
他にも考えてみると ←と→ が増えているのがあります。
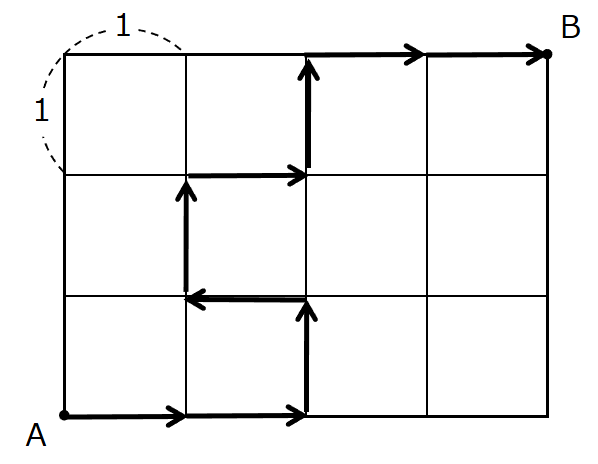
この2種類の遠回りについて調べていきましょう。
できるだけわかりやすく説明するつもりですが、もし少し難しく感じたら(2)を読み飛ばして(3)以降を読んでみてください。
(1)と同様に矢印の並び替えを考えていきます。
↑↑↑→→→→→←の並び替えを考えていきます。
同じ道を通ることができないので→と←が連続になることがないことに気づくと↑←↑と固まりができることが分かります。
この固まりの前後にどの矢印が来るかを下にまとめてみました。
ただし、↑←↑の前後に→が最低一つずつなければいけないことを考慮しています。
| 前の 組み合わせ | 真ん中 | 後ろの 組み合わせ | 前の 並び方 | 後ろの 並び方 | 合計 (前×後ろ) | |
| ① | (→) | ↑←↑ | (↑→→→→) | 1 通り | 5 通り | 5通り |
| ② | (→→) | ↑←↑ | (↑→→→) | 1 通り | 4 通り | 4 通り |
| ③ | (→→→) | ↑←↑ | (↑→→) | 1 通り | 3 通り | 3 通り |
| ④ | (→→→→) | ↑←↑ | (↑→) | 1 通り | 2 通り | 2 通り |
| ⑤ | (↑→→→→) | ↑←↑ | (→) | 5 通り | 1 通り | 5 通り |
| ⑥ | (↑→→→) | ↑←↑ | (→→) | 4 通り | 1 通り | 4 通り |
| ⑦ | (↑→→) | ↑←↑ | (→→→) | 3 通り | 1 通り | 3 通り |
| ⑧ | (↑→) | ↑←↑ | (→→→→) | 2 通り | 1 通り | 2 通り |
それぞれの組み合わせは↑の位置を考えるとすぐに分かると思います。
よって、全部で 5 + 4 + 3 + 2 + 5 + 4 + 3 + 2 = 28 通りです。
↑↑↑↑↓→→→→の並び替えも同様に考えると 63 通りになります。これはぜひ自分でも確かめてみてください。
したがって、28 + 63 = 91 通りが移動距離 7 の全通りです。
(3)の解説
(1)と(2)の答えから移動距離が増えると行き方も多くなるのではと思い、(3)はさらに行き方が多くなると予想する方もいると思います。
そこで、移動距離が12の行き方を(2)と同様に一つ考えてみましょう。
皆さん、何か思いついたでしょうか?実は思いつかなかった人が正解です。
移動距離が11や13の行き方はたくさん見つかるのですが、12のものは見つかりません。
これはなぜでしょうか?
それは遠回りでするさいに←や↓の方向に行くと戻るために逆方向の→や↑を使わなければいけないため、移動距離は必ず2ずつ増えていきます。
そのため、移動距離が9の次に大きいのは11、その次は13となります。
よって、移動距離が12の行き方は0通りです。
(4)の解説
(1)と(3)で7から2ずつ増えた数しか移動距離として表せないことが分かりました。
ただし、無限に増えるわけではありません。
それは同じ道を2度通ってはいけないというルールがあるからです。
それでは、移動距離として表せる最大の数を考えてみましょう。
まず、候補としてすべての道を使う31を考えてみましょう。
これは一筆書きを考えるのですが、攻略法から考えるとこのままだと無理です。
一筆書きを知らなくてもいくつか試してみると難しいことが分かります。
ここから数を小さくしていきましょう。29,27,25と順に調べていくと29と27は見つかりませんが25のものは発見することができると思います。
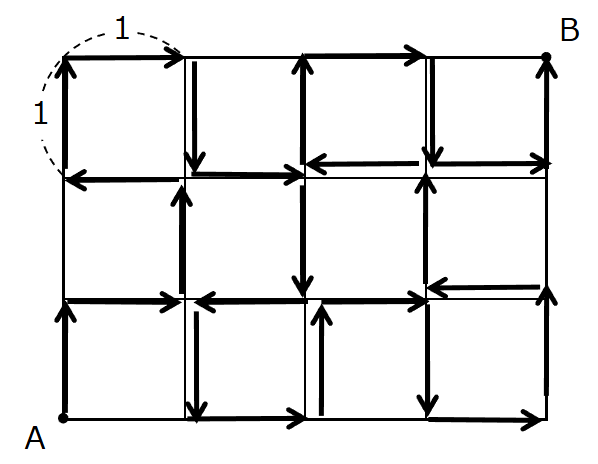
(↑→↑←↑→↓→↓←↓→↑→↓→↑←↑←↑→↓→↑)
さてそれでは本当に7から2ずつ増やして25までは全て表せるのかを考えます。
これは25のものから遠回りを少しずつ減らしていけば、できることが分かると思います。
つまり移動距離として表せる数は7,9,11,13,15,17,19,21,23,25の10個です。
疑問を大事にして「ひらめき」を体験しよう
さて、今回のお話の中ではいくつか疑問から問題を解いている場面があります。
この疑問を持って問題を考えているというのは数学だけではなく、他の学問やパズルなどにも共通していてとても大事なことです。
特に、「なぜ?」や「問題を少しだけ変えたらどうなる?」という疑問は新たな解決の糸口になります。
ぜひ、様々な疑問を大事にして「ひらめき」を体験してみて下さい。
(文責:宇都木一輝)