四角形に隠された不思議な性質５選！

私たちの身の回りには、四角形があふれています。
正方形、長方形、菱形、平行四辺形、台形など、日常のさまざまな場面で目にするこの図形には、実は驚くべき数学的な規則性が隠されていることをご存じでしょうか。
一見シンプルに見える四角形ですが、じつは意外にも奥深く、興味深い性質を持っています。

この記事では、四角形にまつわる特に魅力的な5つの性質をご紹介します。
これらの性質の証明には、中学や高校で学ぶ「中点連結定理」「円周角の定理」「中線定理」などを用いますが、これらを知らなくても、図形の持つ不思議さや美しさを感じていただけるはずです。

①四角形の角度の秘密

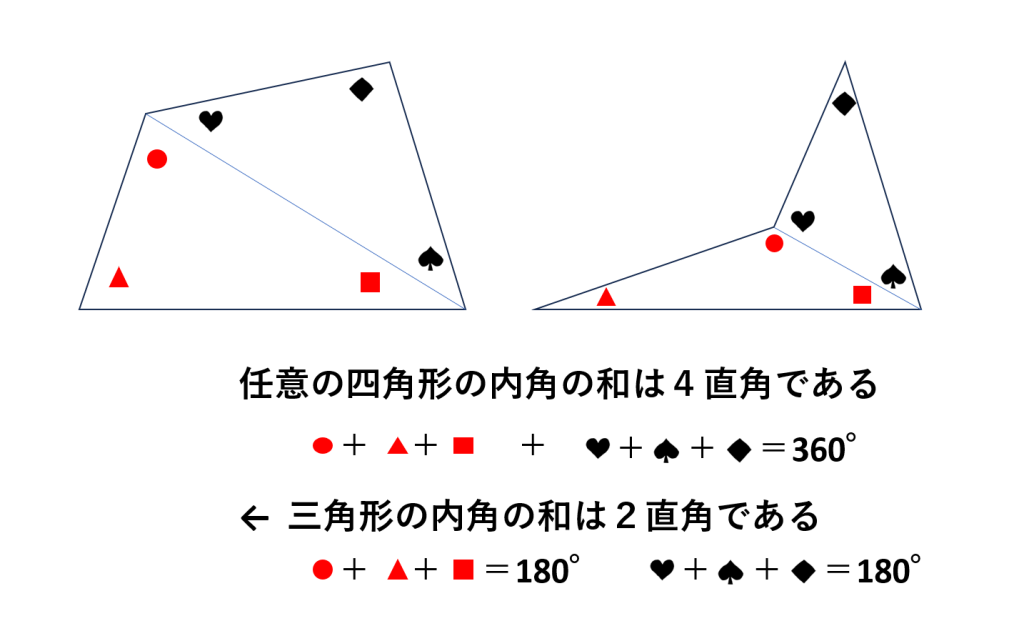
どんな四角形でも「内角の和は360°」になります。
これは、よく知られていることかもしれませんね。
三角形の内角の和が180°であることを利用すれば簡単に説明できます。

四角形の一つの対角線を引くと、三角形が2つできます。この2つの三角形の内角を合計した、180° × 2 = 360°が四角形の内角の和となります。
これは四角形全体に共通する基本的な法則です。四角形が凹んでいる場合（凹四角形）でもこの性質は成り立ちます。形が歪んで見えても、四角形の内角の和は必ず360°になります。

②四角形の中に平行四辺形が現れる？

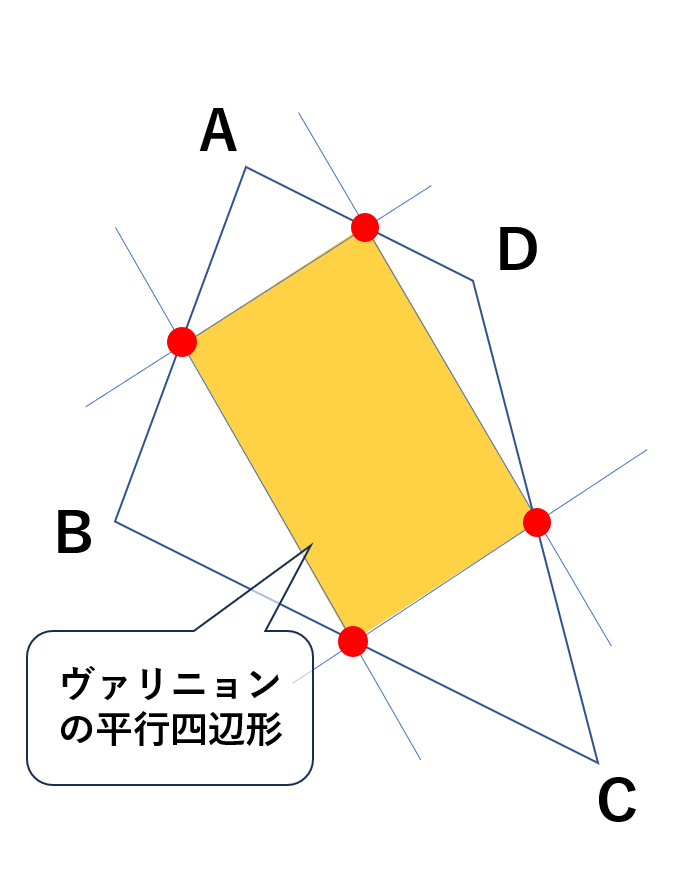
四角形の各辺の中点を順につなぐと、必ず平行四辺形が現れます。
これは「ヴァリニョンの定理」と呼ばれるもので、中にできる平行四辺形は「ヴァリニョンの平行四辺形」といいます。

ヴァリニョンの平行四辺形の面積は元の四角形の面積の半分です。
どんな形の四角形でもこの性質が成り立つため、四角形の中にはいつも隠れた平行四辺形が存在すると言えます。

ヴァリニョンの定理は、中点連結定理を用いて導くことができます。

また、この性質も凹四角形の場合にも成り立ちます。形は崩れたように見えますが、できあがる図形は確かに平行四辺形になっているのです。

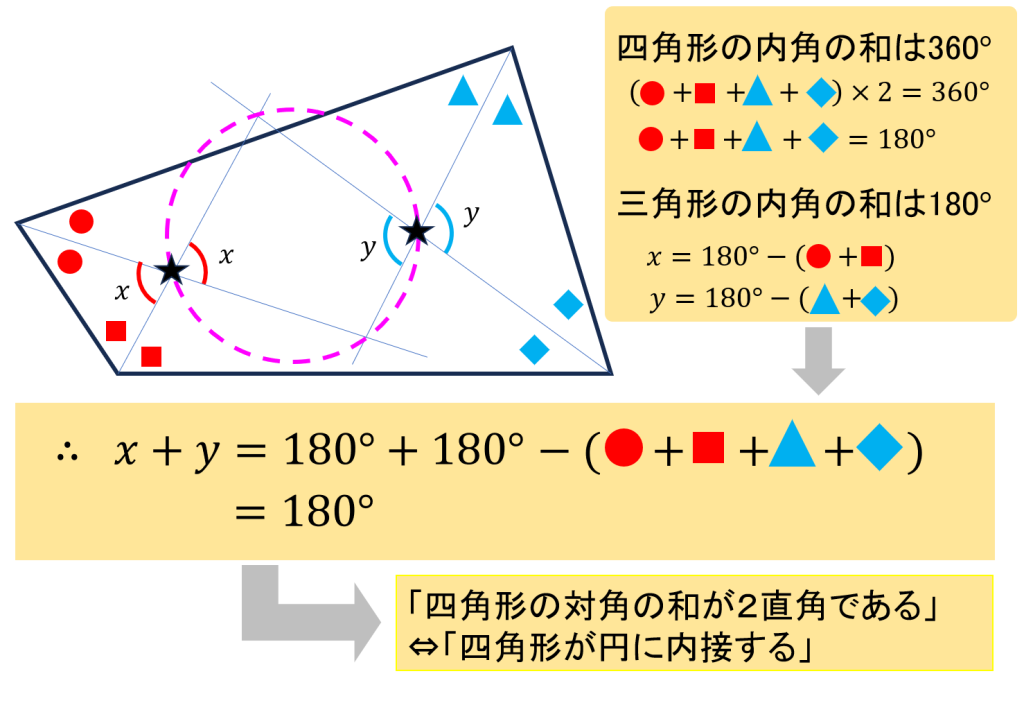
③角を二等分すると円が現れる？

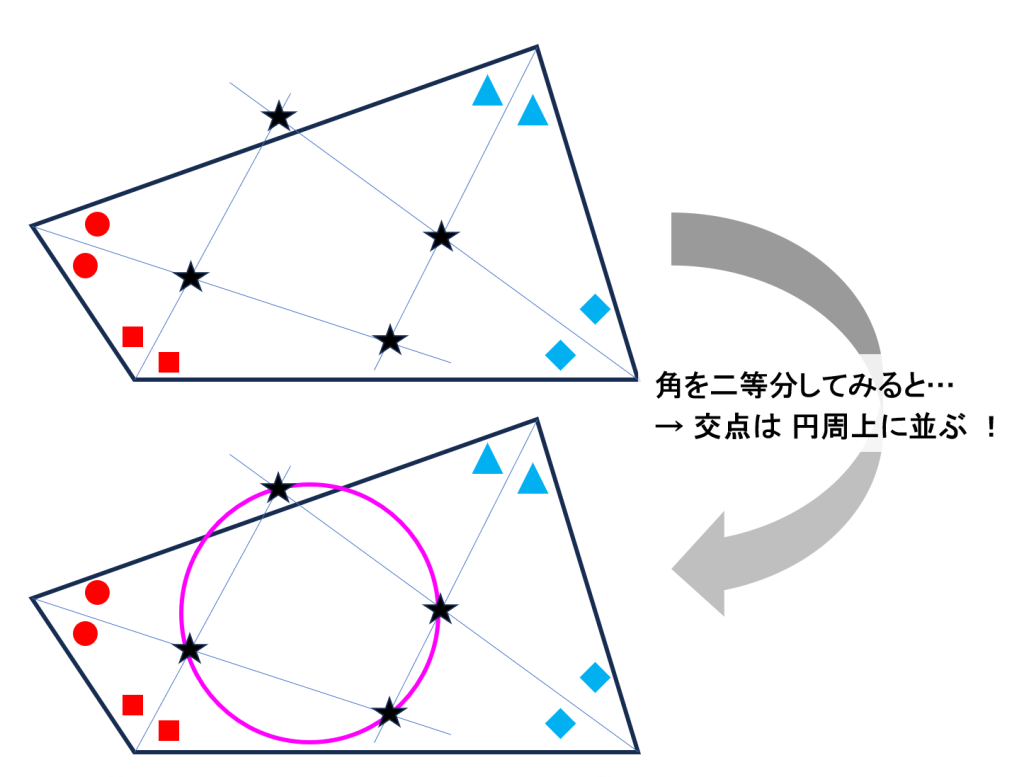
四角形の頂点から二等分線を引きます。
そして、隣り合う頂点から伸びる線分同士の交点に注目します。すると驚くべきことに、その4つの交点は必ず1つの円周上に並びます。

この性質には特別な名前がついていない「名前のない定理」ですが、何の変哲もない四角形から、突然円が現れるため、不思議さが増します。

この定理は、以下の2つの事実

1. 四角形の内角の和は360度である（四角形の角度の秘密で紹介しました）
2. （円周角の定理から得られる内接四角形の性質より）　四角形が円に内接する⇔四角形の向い合う内角の和は180度である

から導かれます。

④正方形を外側に描くと？

四角形の各辺の外側に4つの正方形を描き、向かい合う正方形の中心を線で結ぶと、不思議なことに、それらの線分は直交し、しかも長さが等しくなります。

これは「オーベルの定理」と呼ばれ、四角形の外側にも新たな幾何学的な秩序が生まれることを示しています。

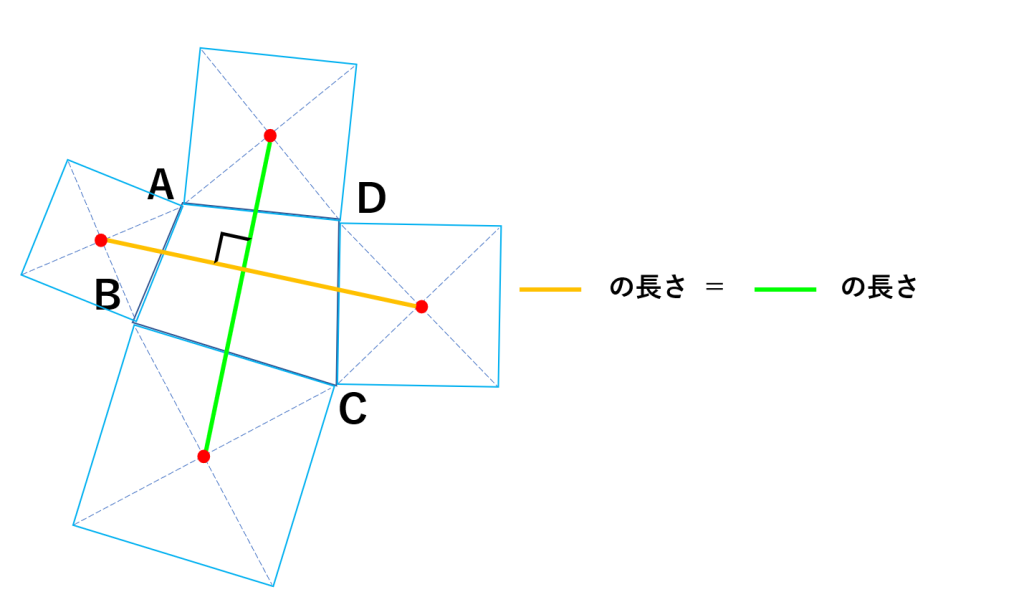
この定理は、いくつかの初等幾何学の定理を用いて証明できるほか、複素数やベクトルといった高校で学ぶ数学的手法でも導かれます。
興味を持った方はぜひ調べてみてください。

初等幾何学による証明は、どのようにしてこの関係に気づいたのかも考えると興味深く思えます。

⑤辺と対角線の長さには法則がある？

一見すると自由に形を変えられそうな四角形ですが、実はその4本の辺と2本の対角線には、図形として成り立つための見えない“束縛”が存在します。

「オイラーの四辺形定理」によれば、4辺の長さの2乗の和と、2本の対角線の長さの2乗の和は、対角線の中点どうしの距離という、ふだんあまり意識しない量を通じて、見事にひとつの式で結びついています。

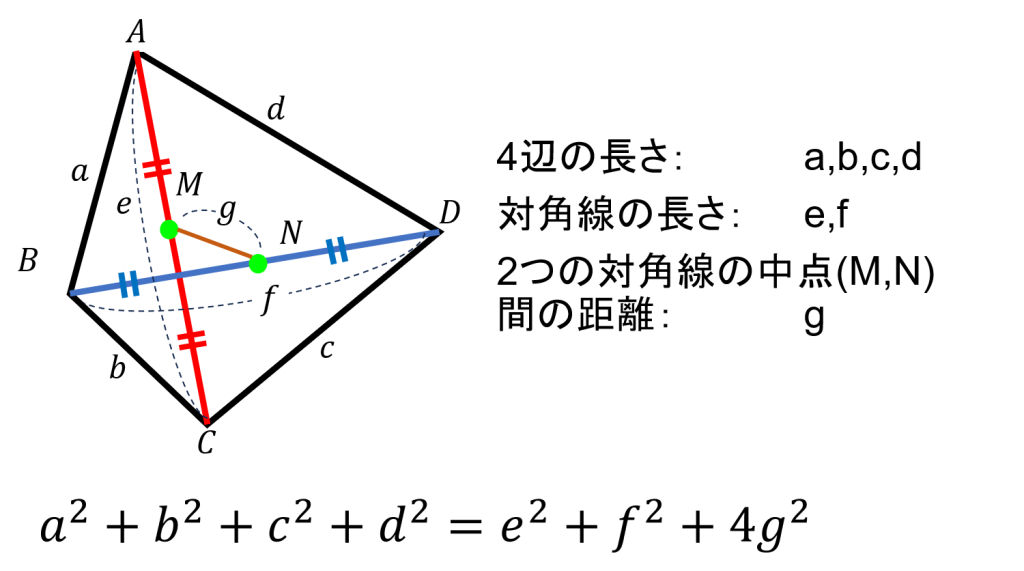
辺や対角線だけでなく、その中点間の距離までもがこの調和に加わっているという事実は、まさに数学の魔法です。何気ない図形の中にひそむこの美しい方程式を知ると、オイラーの発見に感動し、四角形の見え方が変わってくるかもしれません。

四角形は奥深い！

いかがでしたか？
四角形には、今回ご紹介した以外にも、思いがけない法則が数多く隠されています。
単なる4本の線でできた図形と思われがちですが、実は数学の奥深さがぎゅっと詰まっているのです。

これから四角形を見かけたとき、「この形の中には、どんな秘密が潜んでいるのだろう？」と考えてみると、数学の世界がより身近で楽しく感じられるかもしれません。

さらに、四角形がある円に内接していたり、円に外接していたりする場合には、また別の不思議な規則性が現れます。そうした魅力についても、機会を改めてご紹介しますので、どうぞお楽しみに。

（文責：みうら）

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

文系オトナですが、今から数学を楽しめますか？ [ math channel ] 価格：1,760円（税込、送料無料) (2025/7/3時点) 楽天で購入

数学博識王みうらの人気記事　こちらもどうぞ！