こんにちは。中学受験算数ナビゲータの滝澤です。
入試本番が近づいてきました。
今回は中学受験算数指導歴30年以上の経験をもつ私が選ぶ
「簡単なのに人によってはなかなかできるようにならない問題」
を3問ご紹介しようと思います。

弱点克服で大事なのは問題選び
受験も近づいてきたところで、弱点克服のために受験生は一生懸命問題を解いている時期だと思います。
この時期に大切なことは、誰も解けないような難しい問題を解けるように練習することではありません。
- ライバルが解ける問題は確実に解けるようにすること
- 差がつくような問題(正答率が30~40%くらいの問題)をしっかり理解すること
大切なのは、この2点です。
今回ご紹介したいのは、差がつくような問題だと思ってもらってかまいません。
これらの問題は問題演習で何回も出てくるので、子どもにとっては質問しづらい問題とも言えるかもしれません。
先生に「前にも教えただろ!」と言われるかと思うとわかったふりをしてしまう気持ちもわかります。
もし今回の問題の中に「そうそう、これわからなかったんだよ」という問題があったらいいなと思っています。
ではさっそく紹介していきましょう。まずは速さと比の問題です。
1 「歩幅と歩数の旅人算」(速さと比)
【問題】兄が4歩で歩く距離を弟は5歩で歩きます。また,兄が6歩進む間に弟は5歩進みます。
(1)兄と弟の速さの比を求めなさい。
(2)弟が家から100歩歩いたときに,兄が家から弟を追いかけました。弟に追いつくまでに,兄は何歩歩きますか。


この問題の基本的な解法は、「歩幅の比×歩数の比=速さの比」です。
歩数というのは、「同じ時間で何歩進めるか」という意味です。大きな歩幅で同じ時間にたくさん歩を進めれば早くすすめますよね。歩幅の比を考え、歩数の比を考え、速さの比を求めることがまずは基本です。
では解説していきましょう。
解説です
(1)兄が4歩で歩く距離を弟は5歩で歩くので、歩幅の比は5:4です。逆比になることに注意しましょう。
また、兄が6歩進む間に弟は5歩進むので歩数の比は6:5。速さの比は歩幅の比×歩数の比なので、
5×6:4×5=3:2となります。
ここまでは多くの生徒ができます。比を逆に書く凡ミスだけは注意しましょう。
(2) この問題が多くの生徒がなかなかできるようにならない問題です。この問題を図に表すと下のようになります。
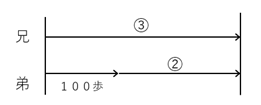
速さの比が3:2なので、兄が歩きはじめてから2人が進む距離は③と②になりますね。
これを見ると、③と②の差にあたる①が100歩ですから③は300歩、答えが300歩のように思えます。
多くの生徒が答えが300歩であると間違えてしまいます。
①の距離を弟が100歩で進むのはその通りです。ですから弟は③の距離を300歩で進みます。
あくまでも「弟は」です。
しかし問われているのは、「兄が」何歩歩くかなのです。
ここで、問題のはじめの文章に戻ってみましょう。
「兄が4歩で歩く距離を弟は5歩で歩きます。」
これが重要なのです。③の距離を弟は300歩で歩きますから、同じ③の距離を兄が何歩歩くかといえば、
4:5=□:300 の□を求めればよいので240歩が答えとなります。
【解答】(1) 3:2 (2) 240歩
速さの問題は「誰が」歩いているのかを常に考えることが大切です。
もう一問、速さの問題を紹介しましょう。速さの問題は多くの学校で出題される単元ですし、得意としている生徒と苦手にしている生徒がそれぞれ一定数いる、最も差がつく単元のうちの1つといっていいでしょう。
2 「○分ごと・○分間隔 問題」(速さと比)
【問題】ある道路を自転車に乗って毎時12kmで走っている人が12分間隔で運転されているバスに20分ごとに追い越されました。バスの時速を求めなさい。また,この人は反対方向からくるバスに何分ごとに出会いますか。


この問題は本当に教えても教えてもできるようにならない問題の代表格です。さらにこの問題は速さの基本の基本をしっかり理解できているかどうかを測ることができる問題です。ですからよく出題されます。さっそく解説していきましょう。
解説です。
まず速さの基本の基本とは「距離÷速さ=時間」という3要素の関係です。
距離・速さ・時間の3要素のうち、この問題でよく理解できないのは、「12分」間隔と「20分」ごとのそれぞれの時間の意味です。
どんな距離をどんな速さでわったものが12分であり、20分なのかが理解できないことが多いのです。ここをしっかり押さえておく必要があります。
「12分間隔」の12分とは、(バスとその次のバスまでの間の距離)を(バスの速さ)でわった時間です。
「20分ごとに追い越される」の20分とは、(バスとその次のバスまでの間の距離)を(バスの速さと自転車の速さの差)でわった時間です。
つまり、この2つの時間は距離が同じなのです。
ですから、(バスの速さ)と(バスの速さと自転車の速さの差)の比が、時間の比の逆比であるとわかります。距離が同じであれば、速さが速いほど、時間は短くなりますよね。よってこの問題では
(バスの速さ):(バスの速さと自転車の速さの差)=5:3
すなわち(バスの速さ):(バスの速さと自転車の速さの差)=5:2となり、
自転車が時速12kmですから、バスの速さは時速30kmとなります。
すると、(バスと次のバスまでの間の距離)は、30km/時×12分=6km になりますね。
反対方向からくるバスに何分ごとに出会うかは、
(バスと次のバスまでの間の距離)÷(バスの速さ+自転車の速さ)で求めることができますから、
6km÷(12km/時+30km/時)=1/7時間=60/7分ごとに追い越されることになります。
【解答】バスの速さ 時速30km 反対方向からくるバスに60/7分ごとに出会う
速さの問題が2つ続いたので、数の性質と規則性の融合問題から1問紹介しましょう。これもなかなか理解が定着しない問題の1つです。
3 「〇や□でわれない数の数列の問題」
【問題】3でも5でもわれない数を順番にならべていきます。
1,2,4,7,8,11,13,14,16,17,19,……
50番目までの合計はいくつですか。

50個くらいであれば全部書いて全部たすという方法で考え方を理解せずに正解してきた生徒もいるでしょう。しかし、その方法ではミスもしやすいですし、500番目と言われたら正解できなくなってしまいます。では解説していきましょう。
解説です
「3でも5でもわれない」と言われたら頭の中に3と5の最小公倍数を思い浮かべられるようになりましょう。15ですね。15以下で、3でも5でもわれない数は次のように8個あります。
1、2、4、7、8、11、13、14
そしてこれらの合計は、1+14.2+13.4+11.7+8と両端から順にたしていくとすべて15になり、15×4=60になりますね。ここまでを1セット目とします。
次に2セット目は16~30まで。実は15以下でさきほど求めた8つの数字(1、2、4、7、8、11、13、14)にそれぞれ15をたした8つの数になります。
16、17、19、22、23、26、28、29
そしてこの8つの数字の和はそれぞれ15ずつ増えているわけですから、60+15×8=180です。
このように考えていくと、次の31~45までの3セット目の8つの数の合計は、180+15×8=300
となることもわかります。
つまりセットごとの合計は、差が120の等差数列になるわけですね。
次にこの問題では50番目までの合計を求めますから、50番目の数が何セット目の何番目の数かを考えます。50÷8=6あまり2 ですから、50番目の数は7セット目の2番目ですね。
6セット目が76~90の数ですから7セット目の2つの数は91と92です。
あとは6セット目まで(60から120ずつ増える6つの等差数列の和)をすべてたせばよいので
60+180+300+420+540+660+91+92=2343
【解答】2343
「理解したふり」はキケン!しっかり練習を
いかがだったでしょうか。これらの問題は多くの生徒が苦手にしている問題ですが、根本を理解してしまえば応用もきく考え方です。
また入試ではこれらの問題を少しひねった問題がよく出題されます。
理解したふりをせずしっかりと得点できるように練習しておきましょう。
公式のように教わる場合もありますが、なぜその公式で解くことができるのかをしっかり理解しておくことが必要です。
これからの学習のコツは、「何をそぎ落とせるか」
入試本番まで決して短い時間ではありませんが、であるからこそ練習する問題はしっかり選んで短い時間で効果的な学習をこころがけましょう。
1問につき10分~15分考えて難しければすぐに解答解説を見て理解するようにすると時間短縮になります。
睡眠時間も大切です。
何を増やせるかではなく、何をそぎ落とせるかを常に考えて本番までの時間を真剣に楽しく過ごしていきましょう。
『線と四角と表でわかる つるかめ算』(日東書院本社)発売中!

「つるかめ算」「和差算」「濃度算」「旅人算」などの特殊算を図解で解説している本『線と四角と表でわかる つるかめ算』(日東書院本社)が発売中です!
文責:滝澤幹
著者プロフィール

タッキー先生(滝澤 幹 たきざわ かん)
中学受験算数ナビゲーター
御三家筑駒中学受験専門塾にて指導歴30年。「算数の楽しさは正解だけではない」「すべての小学生に算数の難問を解く楽しさを知ってほしい」と思い、math channnelに参加。算数表現力ゼミを主催。共著書に『親子で楽しむ!中学受験算数』(平凡社刊)がある。
滝澤先生が選ぶ、中学受験「面白い問題」ベスト3もチェックを!
2022年から2024年まで、中学受験算数で出題された「面白い問題」ベスト3を選んで記事にしています。
ぜひチェックしてみてください。












