こんにちは。中学受験算数ナビゲーターの滝澤です。
早速ですが前回の続きです。前回は開成中学のこの問題をご紹介しました。
問題です
十野くんは1円硬貨と5円硬貨と10円硬貨をそれぞれたくさん持っています。また、五十川くんは1円硬貨と5円硬貨と10円硬貨と50円硬貨を、百山くんは1円硬貨と5円硬貨と10円硬貨と50円硬貨と100円硬貨を、それぞれたくさん持っています。
たとえば、十野くんが20円を支払うとき、硬貨の組み合わせは次の9通りです。

このとき、10円硬貨の枚数に着目すると、
1+3+5=9=3×3
となっていることがわかります。
(1) 十野くんが70円を支払うとき、硬貨の組み合わせは何通りありますか。また、五十川くんが70円を支払うとき、硬貨の組み合わせは何通りありますか。
(2) 百山くんが170円を支払うとき、硬貨の組み合わせは何通りありますか。
(3) ある金額を百山くんが支払うとき、硬貨の組み合わせは 875 通りあります。その金額を五十川くんが支払うとき、硬貨の組み合わせは何通りありますか。また、そのような金額のうち、最も小さいものと最も大きいものを答えなさい。
(2011 開成)
前回の記事で(1)を解説しましたので、今回はこの問題の(2)から解説していきましょう。
第2回のテーマは「解き方なんかない!」です。
わかるとは「分かる」であり「解る」である。
「何通りありますか。」という問題は場合の数と言われる単元の問題です。この単元の問題で、最も重要な考え方は、「問題を分解すべし」という考え方です。
考えてみれば、「わかる」という言葉を漢字にすると「分かる」とも「解る」とも書きますよね。
「わかる」=「分解」なんだなあとわかります。
場合の数では、「~の場合 ★通り」「~の場合 □通り」……などのように様々な場合(パターン)に分けて考える解き方を知っておきましょう。
これを「場合分け」といいます。
(2)は百山くんが170円を支払う方法ですが、まず、100円玉を使わない場合と、使う場合に分けて考えます。
そこからは、50円玉の枚数によってさらに分けて考えていけばよいですね。さらに(1)で考えたことも上手に利用していきましょう。
(2)は、100円玉を使わない場合と、使う場合に分けて考えよう
100円玉を使わない場合、
50円玉が0枚のとき、十野くんが170円支払うのと同じだから、18×18=324通り
50円玉が1枚のとき、十野くんが120円支払うのと同じだから、13×13=169通り
50円玉が2枚のとき、十野くんが70円支払うのと同じだから、8×8=64通り
50円玉が3枚のとき、十野くんが20円支払うのと同じだから、3×3=9通り
100円玉を1枚使う場合、
50円玉が0枚のとき、十野くんが70円支払うのと同じだから、8×8=64通り
50円玉が1枚のとき、十野くんが20円支払うのと同じだから、3×3=9通り
(五十川くんが70円を支払うときと同じだから73通り)
よって 計639通り
解きやすいだけではない!「場合分け」をする意外なメリット
このように場合分けをするメリットは次の2点です。
① 見直しがしやすい。
人間誰でも計算ミスや数え間違いなどはします。それは入試の場合でも同じです。
ですから絶対に必要なのは見直しです。
算数の得意な生徒もテストの最初はミスをしているものです。だからこそ、テストの後半になると必ず「問題を解くモード」から「自分の答案を見直すモード」に頭を切り替えて、一つひとつミスを直していくのです。
そのためには、途中の考え方などは見直しがしやすいものにすべきです。場合分けをしておくと、1つ1つは短い計算や数え上げなので、チェックが楽になります。
② 途中点がもらいやすい。
途中式や考え方を求める多くの中学校では、受験生が書いた答案をしっかり見てくださいます。
そして「この生徒はここまではしっかりわかっているんだな」と伝われば、途中点がもらいやすくなります。
場合の数の問題は完全に正答するのはなかなか大変な単元です。だからこそ、正解はしなくとも得点をしっかり取れるような答案作りを意識することが必要です。
つまり、「自分はここまではわかっていますよ」とアピールすることが必要なのです。
場合分けをすることで、細かく「ここはできている」「わかっている」ということが伝わりやすくなります。
難問が解ける人の発想を鑑賞しよう
次に(3)の解説をしますが、(3)は正答率が低かったと思われます。
入試で場合の数の大問が出題されて、(1)(2)(3)…と小問に分かれている場合、最後の小問については合否を左右しない程度の正答率であることが多いです。
ですから正解する必要はありません。ここからは気楽に、「この問題が解ける人はどのような発想をしているのか」を鑑賞しましょう。
どのような発想をするのか、というと(2)の途中式ででてきた数字に注目するわけです。
18×18、13×13、8×8、3×3という計算をしましたよね。
ここで、18、13、8、3という数字に注目しましょう。5ずつ減っていますね。
この発見が問題を解く発想の種になります。
では(3)にいきましょう。
(3) 百山くんの支払い方が875通りとなる金額を考えるわけですが、ここで必要な発想は「やり方はよくわからないから、調べてみよう!」です。
百山くんが170円を支払うときの「639通り」は、875通りと比較的近いですよね。ですから、「170円より少し大きい金額である180円のときを調べてみよう」と発想するわけです。
あてはめて調べてしまえ!
では、やってみましょう。
百山くんが180円を支払うときは
180を10でわって1加えた数(10円玉が18枚から0枚までだから+1)すなわち19からはじまり、5ずつ減らした数(50円玉の枚数によって、10円玉の枚数は5枚ずつへりますね)、19、14、9、4を2回かけた数の合計となります。
100円玉を使わない場合、19×19+14×14+9×9+4×4=654
100円玉を1枚使う場合、9×9+4×4=97 計751通りです。
残念、これではまだ875通りには届きません。
190円ならばどうでしょうか。
190÷10+1=20 から5ずつ減らした数の15、10、5をそれぞれ2回かけた平方数の和を考えますから
20×20+15×15+10×10+5×5+10×10+5×5=875通りとなりますね。
ビンゴ! 見つけました!
これが「ある金額」のうち最も小さいものであることがわかります。
よってこの金額を五十川くんが支払うときの硬貨の組合わせは
20×20+15×15+10×10+5×5=750通りとなります。
この金額の最も小さいものは190円で、191円、192円、193円、194円までは変わりません。
よって最も大きいものは194円となります。
いかがでしたか。答えはよくわからないけど、「170円より少し大きい金額である180円のときを調べてみよう」という発想。「ひょっとしたら邪道なのでは?」と思った方もいらっしゃるかもしれません。
解き方よりも答えを出したいという意欲が大切
しかし、これはとても大切な考え方なのです。
「解き方がわからないから解けない」と思ってしまう生徒や保護者は多いのですが、それでも答えは出したいという気持ちがありますか?と問いたい。
算数の問題の中には「解き方はわからなくても、勘を働かせて、あてはめていけば答えは出る」という問題は意外と出題されるのです。解き方よりも答えを出したいという意欲が大切なのです。
次回は、桜蔭中学の「変な時計の問題」に挑戦
さて、次回は桜蔭中学の問題を取り上げます。
変わった時計のお話です。
問題です
下の図のようなかわった時計があります。この時計には,7から17までの数字と目盛りが書いてあります。7と8,8と9,9と10,……,16と17の目盛りの間隔は,すべて等しいとします。午前7時を8時0分,午後1時を13時0分のように表すことにします。8時0分のとき,下の図のように時計の長針は7,短針は8を指します。長針と短針は右回りになめらかに動きます。
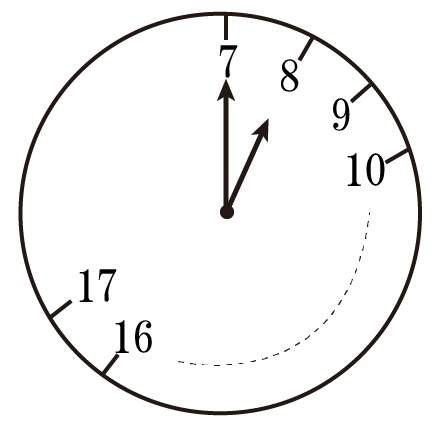
長針は次の①②の規則に従って動きます。
① 長針は7時0分から17時0分までは60分で1周します。
このとき,長針と短針はそれぞれ一定の速さで動きます。
② 長針は17時0分から7時0分までは168分で1周します。
このとき,長針と短針はそれぞれ一定の速さで動きます。
長針が1周する間に短針が回転する角度は,①のときも②のときも同じで,短針は24時間で1周します。
ただし,普通の時計と同じように1時間は60分です。
(1) 次の( )にあてはまる数を答えなさい。
長針が1周する間に短針が回転する角度は( ア )°で 時刻が12時45分のときの長針と短針がつくる角の
大きさは( イ )°です。 ただし,長針と短針のつくる角の大きさは0°以上180°以下とします。
(2) 10時0分から11時0分の1時間で,長針と短針のつくる角の大きさが60°になる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
(3) 17時0分から翌日の7時0分の間で長針と短針が重なる時刻は何時何分ですか。すべて求めなさい。解答用紙の答えのらんは全部使うとは限りません。
(桜蔭中学 2019年)
もし興味がわいたら次回までに解いてみてください。
(文責:滝澤 幹)










