魔方陣の仕組みや作り方について、図解で紹介！～魔方陣に関するアレコレをまとめて解説！～

皆さんは、「魔方陣」という言葉を耳にしたことがありますか。
整然と並んだ数字が、どの方向から足しても同じ数になるという不思議な構造を持つ「魔方陣」。

これは単なるパズルや数学の問題として楽しむだけでなく、歴史や文化にも深く結びついています。

今回のお話では、魔方陣の基本的な仕組みや歴史を簡単に解説し、その魅力を皆さんにお伝えします。
そして、一番簡単な３×３魔方陣の作り方を説明します。

ちなみに、「魔方陣」は「魔法の陣」ではなく、「魔の方陣」です。漢字を間違えないように、お気をつけくださいね！

魔方陣の定義と歴史

まずは、魔方陣の定義について見ていきましょう。

例えば、3行3列の魔方陣では、1から9（＝3×3）の数字を適切に配置し、各行・列・対角線上の数字の和が15になるようにします。
（ここで使用される「行」や「列」という用語は、数学の世界での一般的な呼び方に合わせています）

各行、各列、そして２つの対角線で数字の和が等しくなる値を「定和」と呼びます。
3行3列の魔方陣では、この定和が15となり、4×4の魔方陣では34、5×5なら65、6×6では111というふうに、魔方陣のサイズに応じて定和が決まります。

魔方陣の歴史は、紀元前2200年頃まで遡る！

このような数学的に興味深い構造を持つ魔方陣は、非常に古くから知られています。
その歴史は紀元前2200年頃の中国にまで遡り、当時から魔方陣は数学的な美しさだけでなく、神秘的な力があると考えられていました。
その後、ヨーロッパやインドでも、魔方陣は宗教儀式や占いに使われるなど、単なる数学的対象を超えた象徴的な意味を持つようになります。

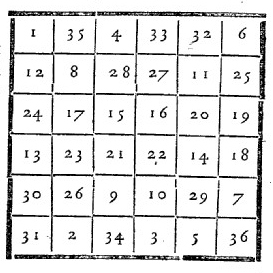
中世ヨーロッパでは、画家アルブレヒト・デューラーが描いた4×4の魔方陣が有名です。

彼の作品には、魔方陣の数学的な精密さと芸術的な感性が融合しており、魔方陣が文化や芸術の中で特別な存在であったことを示しています。
数学と芸術、そして神秘が交わるこの魔方陣の歴史は、時代を超えて多くの人々に影響を与え続けているのです。

魔方陣の種類と定和

次に、魔方陣の種類と定和の求め方について紹介します。

魔方陣の種類

回転させたり裏返したりしても同じ配置になるものは1種類として数えることにします。
そうすると、3×3の魔方陣は１種類となります。
サイズが大きくなるにつれて魔方陣の種類は増加します。4×4では880種類ですが、5×5では、2億7530万5224種類と膨れ上がります。
6×6の魔方陣は、その正確な数を把握することは非常に難しく、おおよその推定値しか求められていません。

定和の求め方

定和の求め方を説明します。

例えば、3×3の魔方陣では、1から9までの数字が使われます。
1から9までの数字の和は45であり、各行または各列の和はすべて等しくなるので、定和は45÷3=15となります。

4×4の魔方陣では、1から16までの数字が使われます。
この場合、1から16までの数字の和は136ですから、それを行（または列）の数である4で割ると、定和は34になります。

定和は使われる数字の和を求め、それを行（または列）の数で割ることで求められることが分かりました。一般化して考えてみましょう。1から△までの数字の和は、（1＋△）×△／2で表されます。したがって、1から○×○までの数字の和は次のように計算できます。

　　数字の和＝（1＋○×○）×○×○／2

これを○で割ると、○×○魔方陣の定和は次の式で表されます。

　　定和＝○×（1＋○×○）／2

このように、具体的な魔方陣の配置がわからなくても、定和を計算できるのは素晴らしいことですね。

3×3の魔方陣の作り方

では3×3の魔方陣を実際に作ってみましょう。

最も素朴な作り方は、マス目の左上から、１、2、3……と順番に数字を並べた配置を作り、それぞれの行、列、そして対角線の数字の和が等しくなるかを一つ一つ確かめる方法です。

しかし、このやり方は非常に手間がかかります。
なぜなら、単に数字を並べるだけで36万2880通り（＝9×8×7×6×5×4×3×2×1）もあり、回転や裏返しを考慮しても、4万5360通り（＝36万2880÷4÷2）あります。
これでは到底やる気が起きませんね。

そこで上手に見つける方法をご紹介します。

まず、2つの対角線上の数字の和と、第2列の数字の和に着目します。
これらの和はすべて15なので、3つ合わせると15×3=45になります。

また、第1行と第3行の数字の和もそれぞれ15ですから、この2行を合わせると15×2=30となります。この2つの差、つまり45−30=15は、何の数字に由来するでしょうか。
そうです、中央のEの数字が3回足されていることによるものです。下の図を見ていただくと分かりやすいと思います。

このあとは、試行錯誤的な手法になります。

まず、Ａ＝1としましょう。すると、Ｉ＝9になります。
したがって、残りの6つの数字｛2,3,4,6,7,8｝から3つの数字を選んでＢ、Ｃ、Ｆに割り当てる必要がありますが、条件としてＢ＋Ｃ＝14、Ｃ＋Ｆ＝6を満たさなければなりません。しかし、これは不可能です。実際にＣの値を決めると、対応するＢやＦが存在しないことがわかります。

次に、Ａ＝2としてみましょう。この場合は、Ｉ＝8となります。
残りの6つの数字｛1,3,4,6,7,9｝から3つの数字を選んで、Ｂ、Ｃ、Ｆに割り当て、Ｂ＋Ｃ＝14、Ｃ＋Ｆ＝7を満たすことができるでしょうか。これは、Ｂ＝9、Ｃ＝4、Ｆ＝3、または、Ｂ＝7、Ｃ＝6、Ｆ＝1で可能です。ここまでできれば、後は簡単です。

実は、Ｂ=7、Ｃ=6、F=1は、回転や裏返しを考慮すると、Ｂ=9、C=4、F=3の場合と同じ配置になることがわかります。

これで、めでたく3×3の魔方陣が出来ました。

おわりに

今回は、『魔方陣事始め』として、定義や歴史、3×3の魔方陣の作り方等をご紹介しました。

魔方陣は非常に奥が深く、例えば、もっと大きなサイズの魔方陣の作成方法や、正三角形・正六角形・円の形をした魔方陣等の興味深い話題が数多くあります。

また、通常の魔方陣では1から連続した数を使用しますが、素数を用いたり、積が同じとなるように並べたりといった特異な形も存在し、独自の魅力を持っています。

さらに魔方陣は数論や代数学、組み合わせ論とも関連があり、数学理論に深い結びつきを持っています。オイラーもラテン方陣という関連する構造を研究し、組み合わせ論に重要な貢献をしました。

これらの話題については、また機会を見てご紹介したいと思います。

なお、3×3の魔方陣の作り方やいろいろな話題については、以下のサイトでも紹介していますので、ご覧ください。

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

数学博識王みうらの人気記事　こちらもどうぞ！