ライターのひろぴかです！
日本で最も有名なおとぎ話の一つである「わらしべ長者」。
ある貧乏な男が藁から始まった物々交換を重ね、最後は屋敷と田んぼを手に入れて裕福な生活を手に入れたという、なんとも夢を見させてくれる話ですよね！
そんな「わらしべ長者」ですが、先日ある考えが浮かびました。『屋敷と田』をさらに物々交換すると、さらに価値のあるものと交換できるのでは……。
そして、
ゆくゆくは日本一のお金持ちになれたのではないか!?
この空想を形にすべく、『宇治拾遺物語』に収められた原作での物々交換を参考に、今回も数学のお兄さんこと横山先生に協力を仰ぎ、わらしべ長者の未来について数学的に検討してみたいと思います！
物々交換で手に入れられる物の価値は、青天井なのか？
ひろぴか早速ですが、それぞれの物々交換における価値の変動はどのように算出していくのがよいでしょうか？
横山当時の通貨などで計算するのは難しいので、現在の金額的価値に置き換え、それぞれの差額について見ていきましょう。
- 作中の物々交換による価値の変化を算出
- 各々の差額から価値上昇率などの法則を定める
- 「屋敷&田」以降、どのような価値の物と交換できるかを推測する
ひろぴかその変化を分析すると法則が見つかるかもしれませんね！
横山ひょっとすると数列や対数的に表せるかもしれません。
- 藁1本 → 蜜柑3個 1円 → 600円
- 蜜柑3個 → 反物3反 600円 → 15万円
- 反物3反 → 馬1頭 15万円 → 300万円
- 馬1頭→ 屋敷&田 300万円 → 3100万円
ひろぴかそれぞれの物々交換の価値について、ざっと算出したところ上記の通りでした。
横山では、それぞれの差額を見ていきましょう。
ひろぴかうーん、一見何の法則も見つけられなさそうですね…。
横山差額だけ見るとそうですね。では、差額の倍率で見てみましょう！
ひろぴかおや。差額の倍率は、段々と減っていますね。
横山反物→馬の変化を見ると、差額の倍率は約1/2倍になっています。
ひろぴか確かに！ 20倍→9.8倍と、約1/2倍ですね！
横山少なくともその倍率差を維持したとすると、次の差額は約4.9倍と推測できます。
ひろぴかなるほど！
横山そうすると、『屋敷&田』の次の交換物の差額は約1.4億円、そして次の交換物は約1.7億円の物と見積もれますね。
ひろぴかあと1回物々交換すれば、大台の1億円に乗ったんだ……もったいない(笑)。でも、その当時に1.7億円の物って何でしょうね？
横山『お宝』とかどうでしょうか？ 宝石などは昔からあったはずですから。
ひろぴかいいですね！ さらなる物々交換で何が手に入るのか楽しみです！
横山同様に考えると推測できます。
暗算するとややこしくなるので、エクセルを用いてみましょう。下の表のように数値を弾き出せます。
ひろぴかすごい！一発で分かりますね！
横山先ほど出した4.9倍の数値が5.05倍になっているなど微小な差はありますが、『お宝』の次は5.4億円の物と交換できることが推測できます。
ひろぴか5億4000万円！
もはや想像できない域になってきました……。
横山ただし、このまま続けても限界は見えてきます。なぜなら、計算を続けると差額の増え方の倍率は段々と減っているからです。
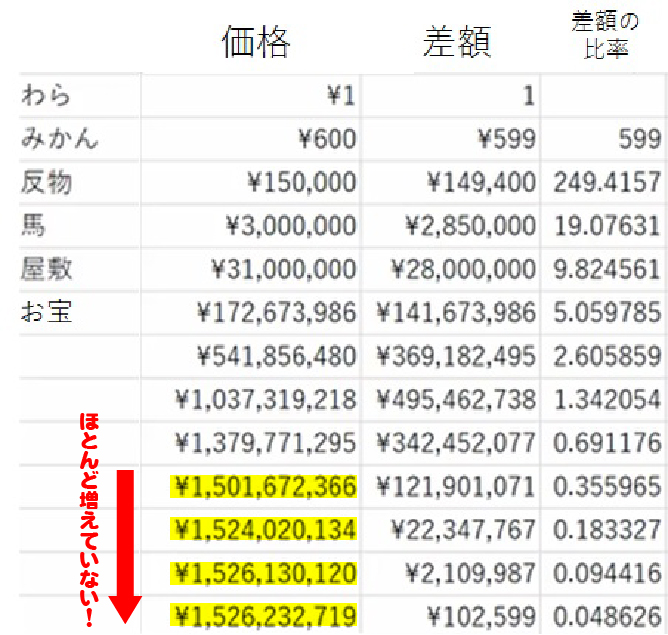
ひろぴか確かに！ 表を見ていくと、『お宝』の3つ先の交換から、増え方の倍率が0.69倍で1を下回っていますね。
横山はい、その段階での物々交換で得られるのは約15億円ですが、そこから先はほぼ増えません。
ひろぴかやはり無限に価格を増やしていくことはできないのですね……。
横山以上から、作中の『屋敷&田』から先を空想すると、あと5回は物々交換しても理に適うという結論が得られますね。
ひろぴか青天井とはいかないんですね(笑)。
『屋敷&田』で物々交換をストップしたのは妥当だった？
ひろぴか無限に増えないとはいえ、作中で主人公の男はもう少し物々交換を試みても良かったのではないでしょうか？
横山そうですね。
ただ、もしかすると物々交換をしていく中で上昇比率がガクンと下がってきたことを感覚的に気づいていたかもしれません。
ひろぴかなるほど！
屋敷あたりでやめとこうと思ったかもしれませんね。
数百倍や数十倍が、いきなり2倍ですから。
横山上昇差額の比が20倍→10倍ときて、そのあと0倍になって何もなくなってしまうかもしれないと考えた可能性もあります(笑)。
ひろぴか確かに！
「欲張ったことで全てを奪われる」っていうのは昔話の定番のオチですから、嫌な予感があったのかもしれませんね(笑)。
横山数学的に考えたのか、物語的に察知したのか(笑)
もしくは、当時は屋敷以上の高価な物が見当たらなかったのかもしれません。
ひろぴか少し調べてみましたが平安時代に5億円以上のものはなかなかないようでした……。そうなるとやはり『屋敷と田』で打ち止めせざるを得なかったのかもしれませんね！
物々交換の数学的な解釈
ひろぴかところで、今回扱った物々交換は数学的にはどのようなジャンルとして見ればよいのでしょうか？
横山これは『数列』になりますね。
その中でも『階差数列』と呼ばれるものになります。
階差数列とは？
ある数列に対し、隣り合う項の差をとることによってできる新たな数列。
ひろぴか高校時代に習ったような気がします！
横山金額自体の変化ではなく、その差額の増え方の比率について考えることで一般化できるという見方ですね。
ひろぴか差額の増え方に注目するのが階差数列ですね！
横山そうです。ここでは、価格は増えるけど、増え方は段々と減ってきて、いずれは変わらなくなる。
ひろぴか金額は増えているからこの先もどんどん増えていきそうに思いますが、差額の増え方に注目するとそうはならないことがわかるんですね。
横山それに、15億円の物を別の15億円の物と交換することはそもそも難しいですし、感覚的に間違ってはいないかと思います。
ひろぴか確かに考えてみると、高額になればなるほど物々交換が難しくなる気がしますね。
横山そうですね。ただ、今回の解釈以外にも別の関数などで考えられるかもしれないので、違う解釈を作れる方がいたらぜひ教えてもらいたいですね(笑)。
まとめ。実は、『わらしべ長者』は身近にある!?
今回は『わらしべ長者』における物々交換を続けた場合、何が手に入るのかを考えてみました。
金額や差額だけ見ていると無限に増えていくように思えますが、数列の考え方を取り入れることで、物々交換には限界があるということがわかりましたね。
気づけてよかった……！
ありがとう数列！
日常であまり触れないと思われる数列ですが、実は今回のようにあるデータから予測を立てることに多く利用されているんです。
例えば、以前は毎日ニュースで見かけていた新型コロナウイルス新規感染者数の予想グラフも数列が用られています。
日々のデータから次の結果を予測するというもので、数は増えているけれども増加率は減っているということがありますが、まさに『わらしべ長者』と似ていますね。
もし、現代で作中の主人公と同じく『屋敷&田』を手に入れた場合、皆さんならどこまでの物々交換を狙いますか？
そういう空想を広げてニヤニヤしたり、数列あるいは別の数学的解釈で物語を分析してみたりすると、『わらしべ長者』の新しい楽しみ方を発見できるかもしれません！
■こちらもどうぞ！
「ヘンゼルとグレーテルの「お菓子の家」に必要なお菓子の量を計算してみた」
