中学受験算数で必須「最大公約数」の求め方～連除法に頼りすぎるとキケン!?～

こんにちは、滝澤です。

中学受験算数では、約数・公約数の問題を小4で学習します。
約数とは、ある整数を割りきることのできる整数のことです。たとえば、18の約数は

1、2、3、6、9、18です。

公約数とは、2種類以上の整数に共通の約数のことをいいます。

18と24の公約数を考えてみましょう。
18の約数が1、2、3、6、9、18。
24の約数が1、2、3、4、6、8、12、24
ですから、公約数は1、2、3、6となるわけです。

このうち、最も大きい公約数のことを最大公約数といいます。
18と24の最大公約数は6になりますね。

小4ではこのように、まずはじめは、基本的には最大公約数を求めるときに、それぞれの約数をすべて書き上げて、共通でなおかつ最大な数を探すという解法を教えます。

これはとても大事な考え方です。1つの数が他のどんな数で割れるのか、また、ある数をかけ算の形に書き換えるとどうなるのか？が数のセンスの根本なのです。

もっと便利な方法もある。それが連除法。

しかし、この解法はそれぞれの約数をすべて書くのが面倒ですね。もっと便利な方法はないものか。そこで、塾などで習う方法が連除法というやり方です。

連除法とはこのような方法です。

1. 2つの数を割り算の逆の形で書きます。
2. 両方の数を割り切れる２以上の数を見つけ、その数で割ります。
3. 商をそれぞれの数の下に書き、また、両方の数を割り切れる２以上の数を探します。
4. 割り切れなくなったら、そこで計算を終了します。　
5. 割り切れる数の積を求めるとそれが２つの数の最大公約数になります。

18と24で連除法をやってみると図のようになります。

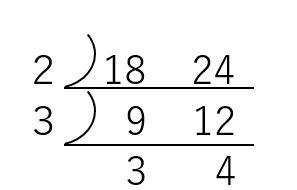
18と24をそれぞれ2で割って9と12になる
→9と12をそれぞれ3で割って3と4になる。
→3と4は、1以外に共通に割り切れる数がないのでここで終了
→割り切れる数として、2と3があるのでこの積を求めて2×3＝6
→よって18と24の最大公約数は6

連除法では解きにくい問題もある。

なるほど。やり方は簡単そうですね。

しかし例えば34と51の最大公約数を連除法で解こうとするとわからなくなってしまう生徒がいます。

34と51を共通に割り切れる数がなかなかわからないのです。
もちろん、両方とも17で割れるということがわかれば、商は2と3になりますから、最大公約数が17であるとわかります。

そう、実は連除法では、共通に割り切れる数の見つけ方はわからないのです。
ですから、最大公約数の求め方として、連除法だけを知っているだけでは不十分なのです。

しかし、最大公約数の求め方として連除法が有名になりすぎていて、この方法しか求め方を知らない生徒も実はたくさんいると思われます。

最大公約数を求める別のいい方法

私がおすすめしているのは、
片方の数の約数を大きい順に挙げ、もう片方の数を割っていくという方法です。

18と24であれば、片方の18の約数を大きい順に考えます。18、9、6、…

これを順に、24÷18、24÷9…と計算して、割り切れれば、
それが最大公約数ということになりますね。
この場合は24÷6＝4で初めて割り切れるので、6が最大公約数ということになります。

34と51でも同様です。34の約数を大きい順に考え、34、17、…
51÷34、51÷17と試すと51÷17＝3と割り切れるので
17が最大公約数であるとわかるのです。

ただ解けるだけではなく計算力もつく

この方法を私がおすすめしている理由の一つに、この方法をくりかえしていると、
計算力がつくということがあります。
約数を大きい順に一つひとつ割れるかどうかを確かめるわけですから、
何度もわり算をしなければいけなくなります。
しかも2けたでわるわり算になることも多いですから、
小4ではまだなかなか慣れていない生徒も多いでしょう。
しかし、小4の算数で一番大事なことは、計算力をつけることであると考えていますので、これは計算が得意になるトレーニングだと思ってがんばってみてください。

最後にチャレンジ問題です。

　「637と1001の最大公約数はいくつですか」

連除法でやるのはなかなか大変な問題かもしれません。共通にわれる数が見つかりますか？
3では割れませんね。7？　そう。7で割ると91と143になります。
これ以上思いつかずに最大公約数は7と答えてしまう生徒もたくさんいます。
じつは、91と143はどちらも13で割れるのです。すると、7と11になって終了。
最大公約数は7×13＝91です。共通に割れる数を見つけるのは大変ですよね。

これも、637の約数を大きい順に、637、91、49、…と考え、

1001÷637、1001÷91、…とやると、1001÷91＝11ですから、
最大公約数は91であるとわかります。

解き方をいくつか知っておくと楽しくなる

中学受験算数では、様々な問題でそれぞれ便利そうな解き方を習います。
しかしその方法は万能ではなく、他の解き方をした方が簡単に解けることも多いのです。
いくつかの解き方を知っておくと算数の楽しさも広がると思います。

（文責：滝澤幹）

『線と四角と表でわかる つるかめ算』（日東書院本社）発売中！

「つるかめ算」「和差算」「濃度算」「旅人算」などの特殊算を図解で解説している本『線と四角と表でわかる つるかめ算』（日東書院本社）が発売中です！

著者プロフィール

滝澤先生のこちらの連載もぜひどうぞ！