パパママ育児お疲れさまです!
お子さんが算数でつまづかないために、日常でできる声かけ働きかけを単元別にお伝えしていきたいシリーズ第8弾!
今回扱う単元は「分数」です。
分数って何年生で習うイメージがありますか?
「ひっくり返してかけるとかわけわからん!」と、最難関の悪名高い!?分数のわり算が印象に残っていて、分数は高学年でしょ?って思う方も多いかもしれませんが……
実は今の教科書では2年生でも扱うようになったんですよ!
といっても、あせる必要はありません。扱うのはごく簡単な分数だけ。むしろ計算を扱う前に登場することで、分数と仲良くなるための期間がたっぷりとれて良い気がします。
そんな2年生に登場する機会もうまく利用しつつ、分数という数に親しむために、おうちでできること・していきたいことは何なのか!?
お話ししていきたいと思います!Let’sgo!

分数が使えるもの、いろいろ!
さて。
おうち分数のポイントは、
とにかく臆することなく、日常でも分数を使っていく。
これにつきます。
「まだわからないんじゃないかな?」とは思わずに、どんどん使ってみて下さい!
わからなかったら……

伝わるように言い直せばいいだけです。
みかん、りんご、ピザ、ケーキ、カステラ、豆腐、卵焼き、のりまき……
分数で表現できるものは、すかさず分数で言っちゃいましょう!!
え?おうち分数って何だよって?そりゃもちろん、「おうちでしれっと子どもに染み込ませちゃう分数教育」の略ですよ?
さあ、
球のかたちのもの

円のかたちをしたもの

筒状、長しかくなどのかたち

東北の美味しいおやつです。私は白いのが好きです。是非ご賞味あれ♪
を切った時は、どうぞ分数で表現してみてください!
そんないきなり……どうしましょう??という方は、こんなふうに段階を踏んでみてはいかがでしょうか?
【LEVEL1】「半分=$\frac{1}{2}$」から始めよう
まずはやっぱり$\frac{1}{2}$!
小さい子でも想像しやすい分数といえば、$\frac{1}{2}$ですよね。
何か子どもと”はんぶんこ”するときに、$\frac{1}{2}$というワードを使っていきましょう!
 パパママ
パパママじゃあ、はんぶんこしようか。
(実際に割って)
 パパママ
パパママはい、〇〇ちゃんも$\frac{1}{2}$、ママも$\frac{1}{2}$。
 キッズ
キッズにぶんのいち?
 パパママ
パパママそ、$\frac{1}{2}$
こんな感じ♪
【LEVEL2】「単位分数」も登場させてみよう
$\frac{1}{2}$に慣れたら、$\frac{1}{3}$・$\frac{1}{4}$など、他の単位分数も登場させてみましょう。
単位分数というのは、分子が1の分数のことです。
(2年生で習うのはこれです。)
例えば6つに切れてる冷凍ピザを食べる時……

 パパママ
パパママパパにも$\frac{1}{6}$だけちょうだい
なんて言ってみたらいいですね。
他にも、
 パパママ
パパママお。このロールケーキ最初から5つに切れてた。親切~!はい、$\frac{1}{5}$本どーぞ。
 パパママ
パパママおかわりちょっとってどのくらい?$\frac{1}{4}$くらい?
などなど。
たくさん分数に触れさせてあげてください。
もし、子どもから説明を求められたら、
「1枚を同じ大きさの3つに分けたとき、そのうちの1つ!これね。これを3分の1っていうんだよ。」
「1本を同じ大きさの5つに分けたうちの1つを5分の1っていうんだよ。」
などと伝えてあげたらいいかと思います。
分数を使い慣れている大人は「同じ大きさに分けたときの」という前提を忘れがちなので気をつけて。
逆に子どもがスルーした場合は大人もスルーしてくださいね。
くれぐれもとっ捕まえて説明しないように(笑)
おうち分数は「しれっと染み込ませる」のが流儀ですからね!
その分数は、量ですか?割合ですか?
そうそう、ここで少し注意したいことが。
分数というのは量を表すのに使う時と、割合を表すのに使う時があるんです。
例えば……
「このカステラ、みんなで$\frac{1}{5}$ずつに分けよう!」
「りんご、食べてもいいけど$\frac{1}{3}$は残しておいて」
「A4のコピー用紙を$\frac{1}{4}$にした大きさの紙を使ってね」
と言った場合には、それぞれ1本のカステラ、1個のりんご、1枚のコピー用紙を等分していて、切り分けた後のものを$\frac{1}{5}$本とか$\frac{1}{3}$個、$\frac{1}{4}$枚と表現することが可能です。
この場合は分数が量を表しています。

対して、
「この場いる人の$\frac{2}{3}$以上の賛成で可決です。」
「これで在庫の$\frac{1}{5}$は捌けたね。」
「ちょっとまって、私のジュース、君の$\frac{5}{6}$くらいしか入ってなくない??」
このような場合、「この場にいる人」「在庫」「君のジュース」をそれぞれ3等分、5等分、6等分しているわけですが、このときの分数は割合を表しています。
この違いを意識できるようでしたら、はじめは量に使う分数に限定してあげたほうが、分数と付き合いやすいのではないかと思います!
ざっくりとした違いとして、「本」や「個」や「枚」などの数助詞がつくかどうかを考えてみて下さい♪
量に使う分数に慣れたら、逆に割合の分数を日常で使ってみせると、これまたしれっと割合の考え方が身について、割合の学習が楽になります!
「茶碗$\frac{1}{4}$杯」などの量に分数を使うのは、もともと1杯という実物があるものを分けているわけではないので、カステラやりんごとは少し毛色が違うものの、「杯」という単位がつけられるぶんイメージがしやすく、両者の橋渡しにちょうどいいかもしれません。

【LEVEL3】実際に切ってみよう
会話の中で$\frac{1}{2}$、$\frac{1}{3}$、$\frac{1}{4}$…などの数を登場させるだけでなく、たまには切れていない何某かを手に入れて、一緒に切り分ける経験もしてほしいなとも思います。
実はコレ、結構できない子が多いんです。
なのでちょっと丁寧にコツを紹介しますね。わかるよって人は飛ばしてください。
今回はピザのような円形のものではなく、カステラみたいな長しかくのものを切ることを想定しましょう。
●$\frac{1}{2}$ずつ
半分ですね。右と左が同じ長さになるように狙いを定めてカット!

●$\frac{1}{3}$ずつ
まずは半分になるくらいの位置に包丁を置き、そのあと少し左(右でもOK!)にずらします。右の長さが左の長さ2つ分になったところ(1:2になるところ)でカット。

●$\frac{1}{4}$ずつ
端から順にカットしようとする子が多いんですがちょっと待って!まず、半分($\frac{1}{2}$)にしましょう!カットしてできた2つをそれぞれ半分にすればOK!
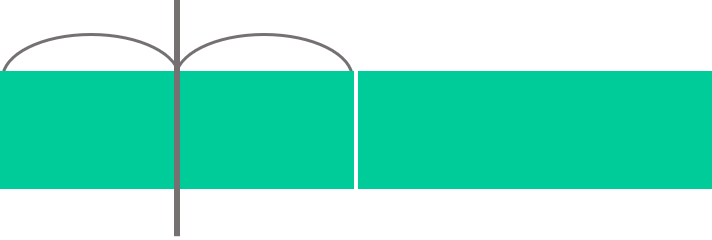
●$\frac{1}{5}$ずつ
こちらも端から切ろうとせず、$\frac{1}{3}$と同様、まずは真ん中に包丁をおいて少しだけ左にずらします。頭の中で右側の長さから左側の長さを引いてみましょう。残りの長さが左の長さの半分になっていればOK。そこで切った後、左をさらに半分にすれば$\frac{1}{5}$になりますね。
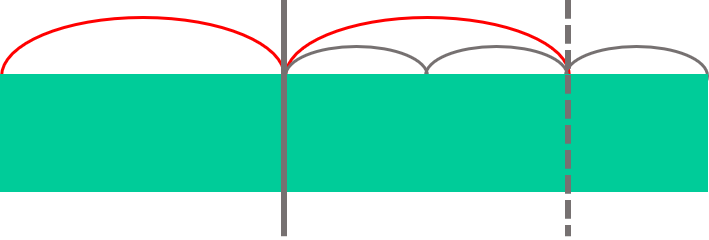
●$\frac{1}{6}$ずつ
分母が偶数の時はまず半分です!$\frac{1}{6}$の場合、そこからさらにそれぞれを$\frac{1}{3}$にすればいいですね。

……いかがですか?
カステラ、豆腐など…まずは$\frac{1}{2}$、$\frac{1}{4}$からはじめてみてくださいね。食品を切ってもらうのに抵抗がある場合は、輪飾りを作る時の折り紙やねん土などで経験できます。
経験するうちに、
「大きい数で分けると、切ったものはちっちゃくなっちゃうね」
なんて発言がでてきたらかなりGOOD!
ちなみに半分にした後$\frac{1}{3}$にして$\frac{1}{6}$を作るというのは、
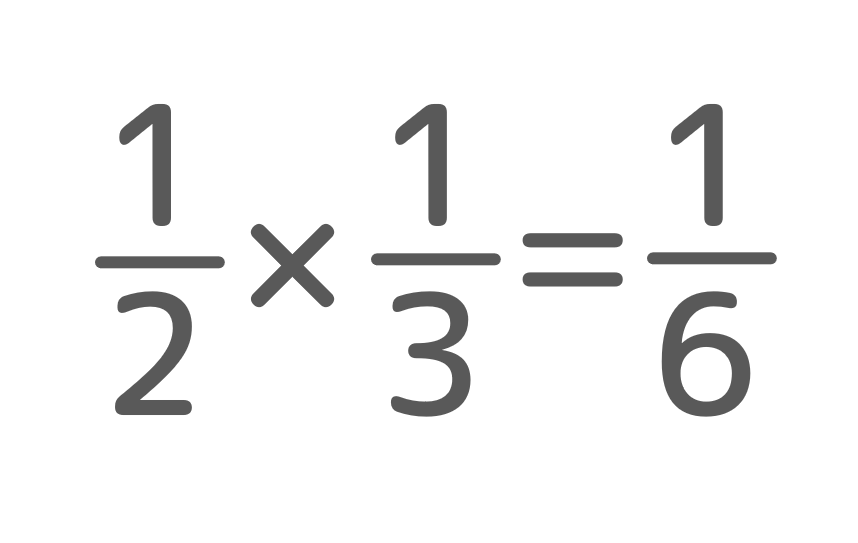
の計算をしれっと体験してたりするんですよ。ナイスしれっとですね?(笑)
【LEVEL4】等しく分けた1つ分に限らず、2つ分でも3つ分でも。
さあ、そろそろ単位分数だけでなく分子が2とか3とかの分数を扱いたくなってきましたね!
さらっと登場していただきましょう!
 パパママ
パパママなし剥いたよ~!
 キッズ
キッズやった~!ひとり何個食べていい?
 パパママ
パパママ8個に切ったから$\frac{2}{8}$個ずつね~!

こんな感じで、分子がいくつかの分数を使っていけばOK。
たいてい子どもは$\frac{2}{8}$枚や$\frac{3}{6}$個を2切れとか3個とかの整数で言いますが、それをあえて分数で表現しなおしてみると、だんだんしみついていきます。
これが十分に馴染んでいれば4年生で習う「分数のたし算ひき算」はきっとすぐ理解できると思いますよ!
【LEVEL5】同じ分数を探してみよう
「等分した大きさのいくつか分」を分数で表現することに十分慣れたら、是非同じ大きさの分数も体感したいところです。
$\frac{1}{6}$ずつに切れているピザをこう配置しなおして…

 パパママ
パパママパパ気付いちゃったんだけどさ、$\frac{2}{6}$と$\frac{1}{3}$って同じじゃね?ほら、こうやってくっつけてみると$\frac{1}{3}$だよね!?
他にも同じものあるかなあ?
みたいに発言できると、$\frac{3}{6}$=$\frac{1}{2}$、$\frac{2}{8}$=$\frac{1}{4}$あたりに気付いてくれるかも!
【LEVEL6】分数÷整数を体験してみる
この辺は、お子さんが分数にノリノリだったらやってみてください。(あまり分数と仲良くなっていないうちから話すと嫌になっちゃうかもしれないので気を付けてくださいね!)
 パパママ
パパママもしこの$\frac{1}{6}$のピザを半分にしたらさ、その大きさは何て言うんだろうね。

 キッズ
キッズ$\frac{1}{2}$じゃないの?
 パパママ
パパママ2つに分けているけど、その前に6つにわけているからなあ…
$\frac{1}{2}$枚って言ったら、こっちじゃない?

 キッズ
キッズじゃあ……$\frac{1}{7}$?
 パパママ
パパママおー!7つに分かれるもんね。
でも全部が同じ大きさじゃないから$\frac{1}{7}$とは言わないだろうなあ。
子どもの中に「?」がでてきたらそれでOK。無理に正解まで教える必要はありません。事実、数日経ってから「あの時のさあ……」なんて子どもから話し始めることはよくあります。
もちろん正解がでてくるパターンも!
 キッズ
キッズ$\frac{1}{12}$だよ
そんな時は考えを聞いてみて下さい。
 パパママ
パパママえ?どうして?
 キッズ
キッズこれって、6つにわけたピザ全部を2ずつにわけた大きさだから12こにわけてるでしょ?
 パパママ
パパママほ~!確かに!$\frac{1}{6}$を2つに分けると$\frac{1}{12}$になるのかあ~。(しれっとまとめ)
ばっちり理解できてますね。
逆に理由に詰まるようなら、無理に聞き出さなくてOK。
「説明は難しいよね~。でもなんか$\frac{1}{12}$、いい気がする!12こに分かれるもんね。」ぐらいにとどめてみましょう!
【LEVEL7】整数÷整数を体験してみる
整数と整数のわり算って、どこが分数やねん!と思うかもしれませんが、2÷5=$\frac{2}{5}$などのパターンのやつです。
子どもとこの場面の話をするには、まず、2種類のピザを作ります←
そして、家族(この場合5人とします)で切り分けながら呟きましょう。
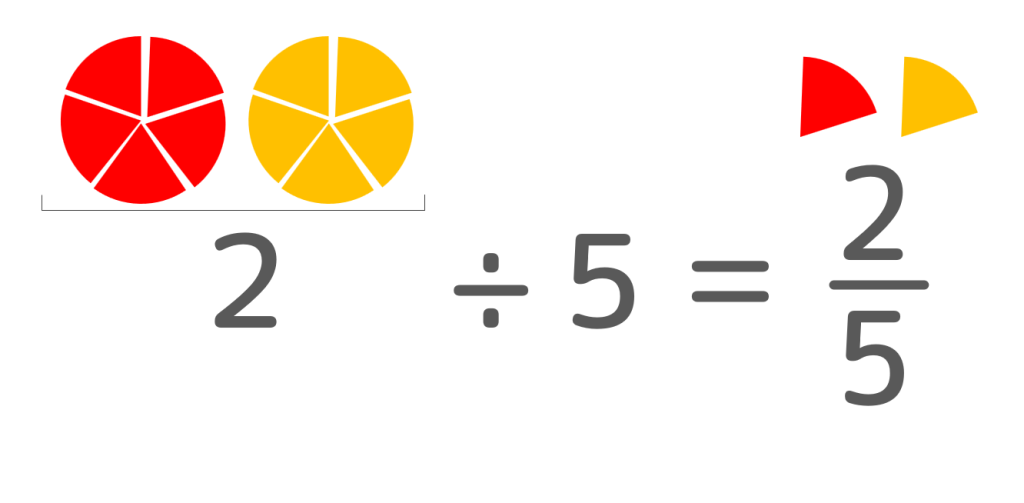
 パパママ
パパママこれでどっちも$\frac{1}{5}$ずつにわけられて、みんなマルゲリータとクワトロフォルマッジの両方食べれるように配るから、$\frac{1}{5}$と$\frac{1}{5}$で1人分は$\frac{2}{5}$じゃん?
 パパママ
パパママ2!まいを5人でわけたら、1人分が5ぶんの2!って、2と5がでてくるの面白いね~
以上!
他の分数の計算についても、なんならおうちの方が探究しなおす気分で気付きを発言すると、お子さんも「なになに!?」ってくいついてきてくれると思います。それぞれの意味がわからなくても、なんだか分数は美味しいし面白い!ってイメージがつくといいですね!
いかがでしたでしょうか?
LEVEL5以降は上級者向けではありますが、すこーしずつ慣れて、こういうことが考えられると分数の計算もやり方ではなく原理から分かるようになります。
分数と仲良くなるには少し時間がかかると思うので、おりをみてピザを食べて……違うか。分数チャンスをみつけて、親も楽しむつもりで触れ合ってみてください!
こちらの記事にもおうちで分数を楽しむヒントをまとめています。
よかったら見てみてくださいね♪
それでは、今回はここまで。
次回は「長さ」についてお話します。お楽しみに!

■バックナンバーはこちら!










