中学入試の算数指導歴30年の滝澤です。
2024年の中学受験が、2月にほぼ終わりました。苦しい時を乗り越え,目標に向かって一生懸命戦ったすべての小学6年生のみなさん、そして保護者のみなさん、塾や中学校の先生方、お疲れ様でした。
いつもミスだらけだった生徒が本番でノーミス
うちの塾では合格者に合格作文をお願いしているのですが、今年心に残る作文を書いてくれた生徒がいました。彼女は桜蔭に合格した生徒だったのですが、算数が決して得意ではない生徒でした。特に彼女は凡ミスが多かった。ミスといっても「書き間違い」、「繰り上がりや繰り下がりミス」、「掛け算の暗記ミス」「比の順番を逆にするミス」「植木算や日数計算の+1忘れ」など、多種多様でした。そこで私が渡したミス撲滅プリントをすべて言う通りやってくれて、本番の桜蔭の入試では凡ミスが1つもなかったというのです。
そのプリントを元に彼女がやったこととは大きく3つです。
- 猫背をやめて姿勢よくテストを受ける。
- 左手(利き手ではないほう)をそえて答案を書く。
- ゆっくりていねいに文字や図をかく。
こんなことでミスがなくなるのかと半信半疑だったようですが、実際に効果はあったようです。しかしこれをやるのはかなり面倒です。なによりもミスをなくすようにどんな面倒なことでもおろそかにせずやりきるという覚悟を決めることが大切です。参考にしていただければ幸いです。
2024年の中学受験算数の「面白い問題」
さて、今年も多くの算数の面白い問題に出会うことができました。今回はその中でも、有名中学の出題の中から面白い問題ベスト3を選んでみたいと思います。
面白い問題とは、私なりの「面白い」の判断基準ですが、
- 小4・小5でもチャレンジできる単元・難易度のもの
- 解法の知識などがなくても試行錯誤をくり返した末に答えを導き出せるもの
- 手間がかかりそうだけど,工夫によって簡単に解けるもの
などが挙げられます。
ではさっそく、第3位から参りましょう。
第3位 開成中学 1(1)
【問題】数字1,2,3,4,5,6,7,8,9と四則演算記号+-×÷とカッコだけを用いて2024を作る式を1つ書きなさい。ただし、次の指示に従うこと。
①1つの数字を2個以上使ってはいけません。
②2個以上の数字を並べて2けた以上の数を作ってはいけません。
③できるだけ使う数字の個数が少なくなるようにしなさい。
(使う数字の個数が少ないほど,高い得点を与えます)
開成中はこのような計算パズルを出題することがたまにあります。
「3,4,7,8と四則演算記号+-×÷とカッコだけを用いて答えが1~10になる式をすべて書く」
という問題も出題されています。
2024年の1番のとても面白いところは指示③の
「使う数字の個数が少ないほど,高い得点を与えます」
というところですね。答えはいくつもあるけれどもできるだけシンプルな美しさを求めているということになるでしょう。
さっそく解説をしていきましょう。
解説
1けたの数字をできるだけ少なく,計算の答えを4けたの2024という大きな数の答にするためには、+-×÷のうち、できるだけ,かけ算を使った方がいいですよね。というわけで2024を素因数分解してみましょう。
2024=2×2×2×11×23
1つの数字は1個しか使えませんから、2×2×2=8として、「2024=8× 11 × 23」 をもとに考えた方がよさそうですね。では、11と23を1けたの数の計算で書き表してみましょう。
11⇒2+9,3+8,4+7,5+6
23=24-1=3×8-1=4×6-1
などが考えられます。これらを組み合わせると
2024=8×(2+9)×(4×6-1)
という式が考えられますね。これも1つの解答です。
しかし、これだと使った数字は6個ですね。
もっと少ない数字で作れないでしょうか?
次に「2024=8×253」と考えて、253が答えとなる式をできるだけ少ない個数の1けたの数字で式に表すことを考えてみましょう。
9×7×6=378、9×7×5=315、9×6×5=270、9×7×4=252、…
252は253にかなり近い数字ですね。253=9×7×4+1と表すことができます。
ですから、
2024=8×(9×7×4+1)
これならつかった数字は5個なのでこれが模範解答になります
模範解答は 8×(9×7×4+1)
実は…2024の年号問題、別の学校で予想的中!
この問題は2024という年号の数字を使った問題ですね。
実は私はこのタキザワ流のブログ記事のなかで昨年末に2024を使った問題をいくつか予想していました。
この開成の問題は「予想しようと思えばできたな」と少し悔しく思いました。
でも、実は今年2問を的中させることができました!!
①栄東東大特待Ⅱの入試問題が予想的中!
<予想した2024問題>
次のように0、2、4だけを小さい順に書いていきます。
2、4、20、22、24、40、42、44、200 、……
次の問いに答えなさい。
(1)省略 (2)2024は何番目ですか。
<栄東東大特待Ⅱで出題された問題>
0,2,4の3つの数字を使って、
2,4,20,22,24,40,42,44,200,……
と小さい順に数をつくっていくと、2024は( ) 番目です
②高槻中学の入試問題が予想的中!
<予想した2024問題>
2024をいくつかの連続する整数の和で表します。このとき初めの数とその個数の組をすべて求めなさい。ただし、10,11,12,13,14,15のとき(初めの数が10で個数が6)のときは、(10,6)と答えなさい。
<高槻中学で出題された問題>
ある整数Aから始めて,1ずつ大きい整数を足したところ,B個の整数の和となり2024になりました。Bが3以上25以下の奇数であるとき,考えられるAとBの組は2通りあります。その2通りのAとBの組(A,B)を求めなさい。(後略)
生徒さんにも喜んでいただきました!
どちらの問題もほぼ完全にあてていると言ってもよいでしょう。しかもうれしかったのは、どちらの問題も実際に受験された生徒さんから「先生が予想した問題が出ました!おかげで正解できました!」と報告していただいたということです。これ以上の喜びはありません。
2025年も知恵をしぼって予想しようと思っております。
さて、ではベスト3の紹介にもどりましょう。
第2位 攻玉社中学第3回
次のA、B、C、D、E、F、Gの図形は、面積が1cm2の4つの正方形を辺どうしがぴったり重なるようにしてつなげてできる図形です。
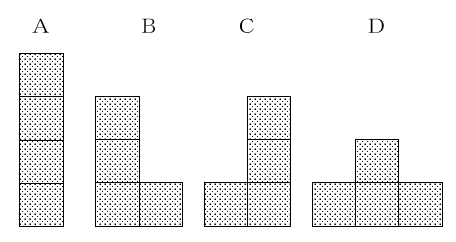
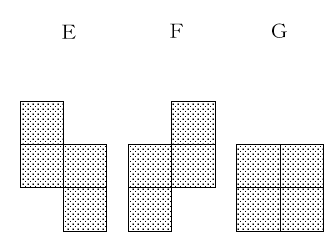
この7種類の図形のうち、1種類だけ2個使い、残りの6種類は1個ずつ使って、縦4cm、横8cmの32マスの長方形を埋めていきます。
ただし、A~Gの図形は回転させてもよいですが、裏返してはいけません。
32マスの長方形をすべて埋めるためには、A~Gのうち( )を2個使う必要があります。下の白と黒で塗り分けられた図を参考にしなさい。

いかがでしょうか。試験会場で実際にこのようなパズルを考えなければいけないのでしょうか。
実はこの問題、A~Gのピースを組み合わせてどのように長方形を埋めるかを考えることなく解くことができます。
そのための「白と黒で塗り分けられた図」なのです。
解説
解説しましょう。まず、A~Gのピースを白と黒で同じように塗り分けます。
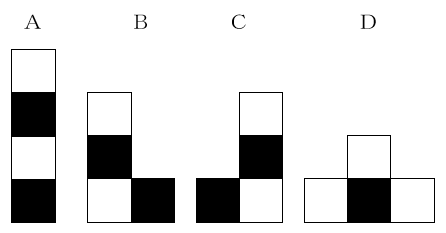
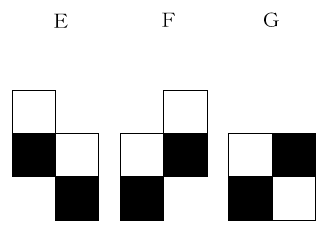
このようにすると1つだけ仲間はずれの図があるのがわかりますか。そう、Dの図だけが、白と黒の個数が違いますね。他はすべて白と黒の正方形が2個ずつになっています。
ここで、白と黒で塗り分けられた32マスの長方形を見てみると、白と黒の長方形の個数は同じですよね。ということは、Dを2種類使わなければ埋めることができないとわかるわけです。
Dの片方は白3個黒1個、もう片方は白1個黒3個の正方形になるわけですね。このように正方形を2色で互い違いになるように塗り分けた模様を市松模様といいますが、これを使ったとても面白い問題でした。
似たような問題で、白と黒で塗られたマスが交互に並んでいる7×7マスのチェス盤と駒の「ナイト」の動き方についての問題が浅野中学で出題されています。
第1位 豊島岡女子学園中学
下の図の直角三角形PQRと正方形STUVがあります。辺QRの長さと正方形の1辺の長さが等しく,辺PRの長さと正方形の1辺の長さの和が4cmであるとき、2つの図形の面積の和は何cm2ですか。
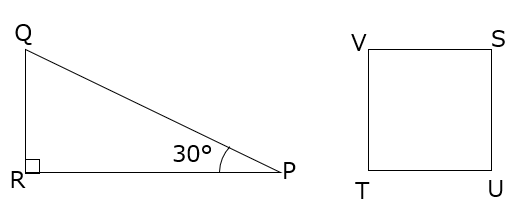
とても美しい問題です。正三角形の半分である直角三角形と正方形の面積の和を求める問題なのですが、わかっている長さは、辺PRの長さと正方形の1辺の長さの和が4cmであることだけです。
中学生になれば、30°60°90°の直角三角形の辺の長さの比が1:2:√3であることを習うので、数学の平方根の知識を使えば、すべての辺の長さを√を使って求めることができるので、解けるといえば解けるのですが、わりと面倒な計算になってしまいます。
しかし、算数で解くととても簡単に解けてしまうのです。では解説していきましょう。
解説
長さが1つしかわかっていなくても面積が出せる形と言えばまず思い浮かぶのが正方形です。この問題では、1辺が4cmの正方形をイメージすることが大切なのです。
また、直角三角形PQRは2つ並べると正三角形ができますから、辺PQの長さが辺QRの長さの2倍で、辺QRの長さと正方形の1辺の長さが等しいことから、辺PQの長さは正方形の1辺の長さの2倍であることもわかります。
さらに、辺QRの長さと正方形の1辺の長さが等しく,辺PRの長さと正方形の1辺の長さの和が4cmということは、辺QRと辺PRの長さの和は4cmということですね。
これらのことから、次のような図を描くことができます。
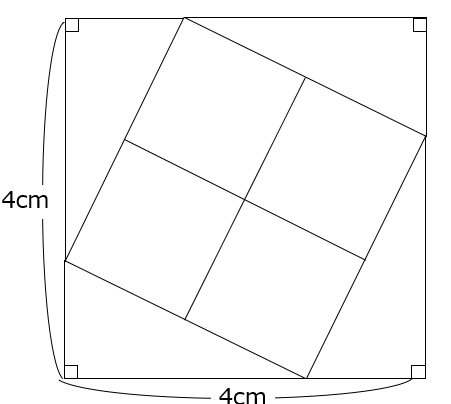
正方形4つと直角三角形4つを組み合わせて1辺4cmの正方形ができますから、
求める面積の和は、4×4÷4=4cm2とわかりますね。
算数の楽しみ方はさまざま
いかがでしょうか。この解法のシンプルな美しさがおわかり頂けますでしょうか。もちろんこの解法でなければいけないということはありません。他にも直角二等辺三角形を利用した解き方もありますし、様々な解き方があります。算数は解き方も楽しみ方も様々です。
ひょっとしたら、この問題は難しい問題と感じる方もいらっしゃるかもしれません。こんな解法を思いつかないよと思う方もいらっしゃるかもしれません。けれども、自分で解けなくても解答解説を見たときになにか感動をおぼえる、これも算数の1つの楽しみ方だと私は思っています。
自分で解けたわけでなくても、解説を見るだけで楽しいという感覚が身についてくると、算数はもっと楽しくなります。
正解することだけに価値があるのではなく、解き方の楽しさ・美しさを感じられる中学入試算数の問題をこれからも紹介したいと思っています。
滝澤先生オススメの面白い問題を集めた「おもしろ中学受験算数講座」が毎週受講できます!
math channelでは、滝澤先生オススメの面白い中学受験算数の問題を集めた「おもしろ中学受験算数講座」をオンデマンドで開講しています。
自分の好きなタイミングで受講でき、添削もできます!
過去の「面白い問題ベスト3」もチェック!
滝澤先生がこれまでに選んだ「面白い問題」もぜひチェックしてみてください!
2023年はこちら
2022年はこちら
(文責:滝澤幹)