三角形の“心”にせまる【その２】〜垂心・内心・外心をチェバの定理で解き明かす〜

こんにちは、みうらです。

前回（その1）では、三角形の“心”と呼ばれる特別な点のうち、重心に注目し、その共点性がなぜ成り立つのかを「チェバの定理」を使って明らかにしました。

今回はその続編として、垂心・内心・外心という三角形の他の“心”についても、同様にチェバの定理を用いて、その共点性を明らかにします。

これらは重心に比べて構造がやや複雑ですが、数学的なつながりが明確になるほど、図形の奥深さと論理の美しさをより一層感じていただけるはずです。

それでは、順に見ていきましょう。

垂心の共点性

まずは、垂心についてです。

三角形ABCの各頂点から対辺に下した垂線と辺の交点を以下のように定めます：

• AからBCへ下した垂線との交点 → D
• BからCAへ下した垂線との交点 → E
• CからABへ下した垂線との交点 → F

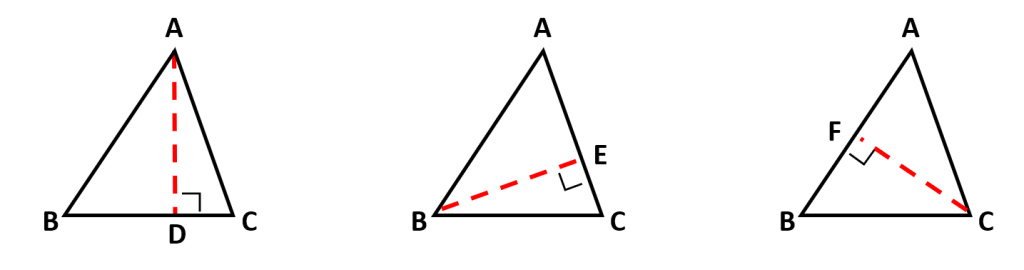
次の相似な直角三角形の性質を利用します：

• △ADC ∽ △BEC ⇒ CE /DC = BC / CA　…　①
• △ADB ∽ △CFA ⇒  BD /FB = AB / BC　 …　②
• △CFA ∽ △BEA  ⇒ AF / EA = CA / AB　…　③

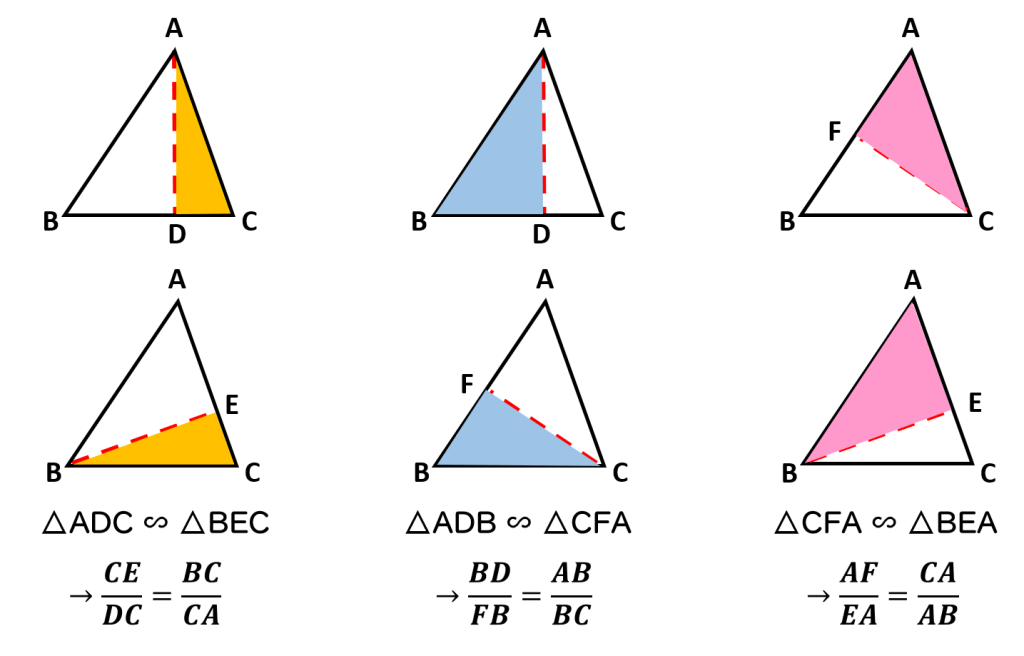
①②③を辺々掛けると

$$\frac{CE}{DC} \times \frac{BD}{FB} \times \frac{AF}{EA}= \frac{BC}{CA} \times \frac{AB}{BC} \times \frac{CA}{AB}$$

左辺の分子と分母の並びを入れ替えると

$$\text{左辺} = \frac{AF}{FB} \times \frac{BD}{DC} \times \frac{CE}{EA}$$

そして、

$$\text{右辺} = 1$$

したがって、3直線AD, BE, CFは一点で交わります。これが「垂心」です。

内心の共点性

続いて、内心です。

各内角の二等分線と対辺の交点を定めます：

• 角Aの二等分線とBCの交点 → D
• 角Bの二等分線とCAの交点 → E
• 角Cの二等分線とABの交点 → F

角の二等分線の性質により：

• BD / DC = AB / AC
• CE / EA = BC / AB
• AF / FB = AC / BC

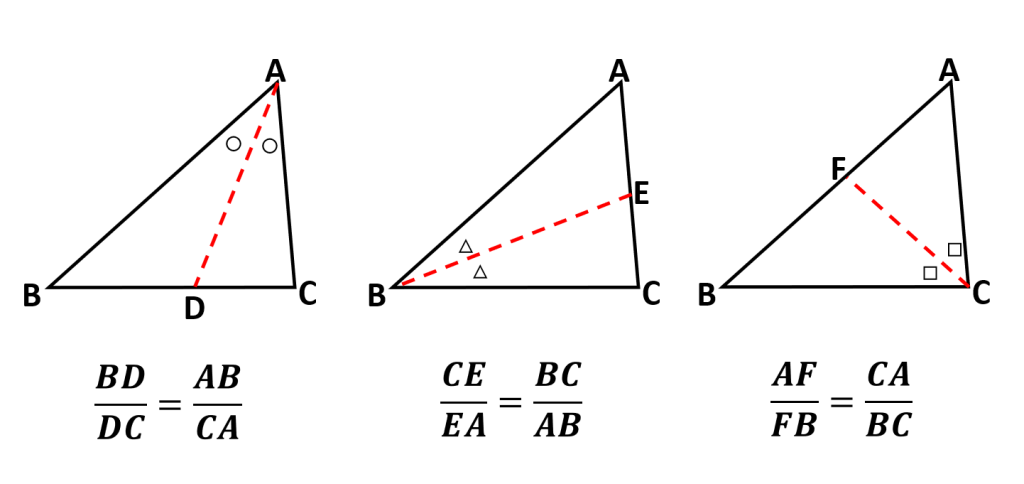
したがって、

$$\frac{AF}{FB} \times \frac{BD}{DC} \times \frac{CE}{EA}= \frac{AC}{BC} \times \frac{AB}{AC} \times \frac{AC}{BC} = 1$$

ゆえに、3本の角の二等分線は1点で交わります。
この点が「内心」であり、三角形の内接円の中心です。

外心の共点性

最後に、外心です。

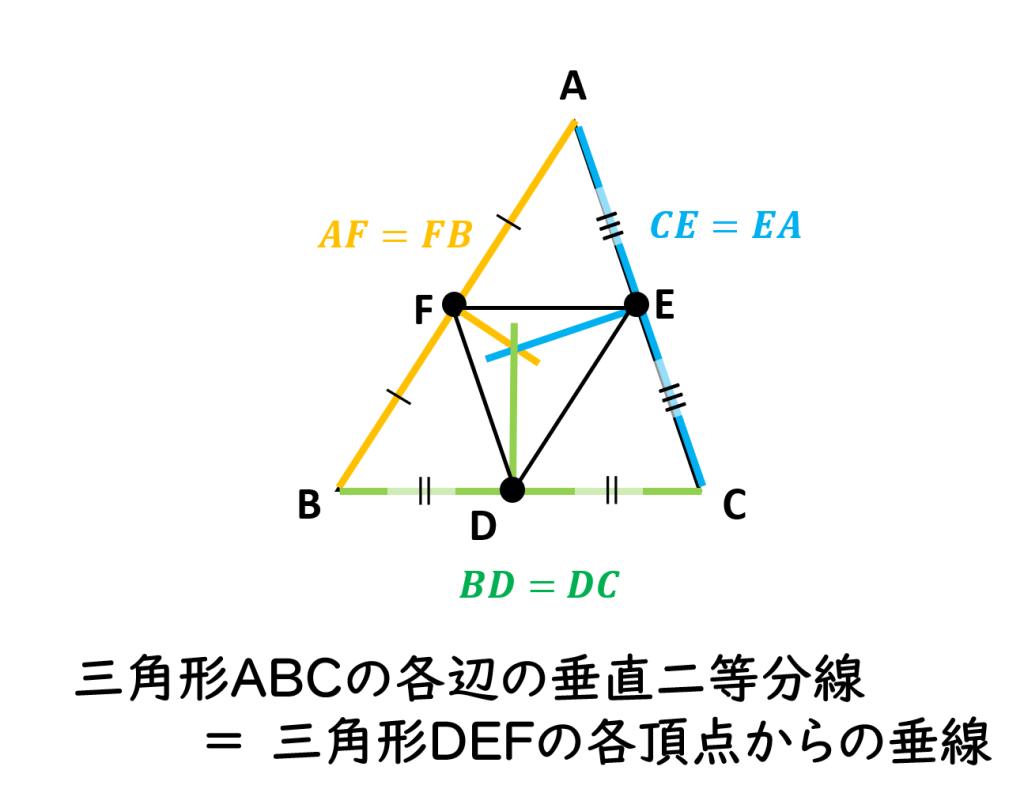
三角形ABCの各辺BC, CA, ABの中点をそれぞれD, E, Fとします。
このとき三角形DEFを考えると、三角形ABCの各辺の垂直二等分線は、三角形DEFの各頂点からの垂線と対応します。

三角形DEFの垂線は1点に交わる（＝DEFの垂心）ことから、対応する三角形ABCの垂直二等分線も1点に交わることが導かれます。

この交点は、三角形の3頂点すべてから等距離にある点であり、「外接円の中心＝外心」です。

おわりに

こうして、重心・垂心・内心・外心という三角形に特有の4つの“心”は、すべてチェバの定理によって、その共点性が数学的に説明できることがわかりました。 実はこうした「共点性」は、これら4点だけでなく、他にも「ジュルゴンヌ点」や「ナゲル点」といった、不思議に交わる点が存在します。
三角形の内部構造には、まだまだ奥深い数学が眠っているのです。

次回【その３】では、こうした他の共点（ジュルゴンヌ点、ナゲル点）を取り上げます。
より深く、より豊かな三角形の“心”の世界にご期待ください！

（文責：みうら）

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

文系オトナですが、今から数学を楽しめますか？ [ math channel ] 価格：1,760円（税込、送料無料) (2025/7/3時点) 楽天で購入

数学博識王みうらの人気記事　こちらもどうぞ！