計算がほぼいらない⁉図形パズルで「三平方の定理」を使いこなそう！【前編】

こんにちは、みうらです。

皆さん、「三平方の定理（またはピタゴラスの定理）」と聞くと、聞いたことがあるという方が多いのではないでしょうか。

今回ご紹介するのは、このピタゴラスの定理を使った、ちょっとした図形のパズルです。
ほとんど計算は不要です。基本となるいくつかの図を理解し、それを使えば解ける問題ばかりです。

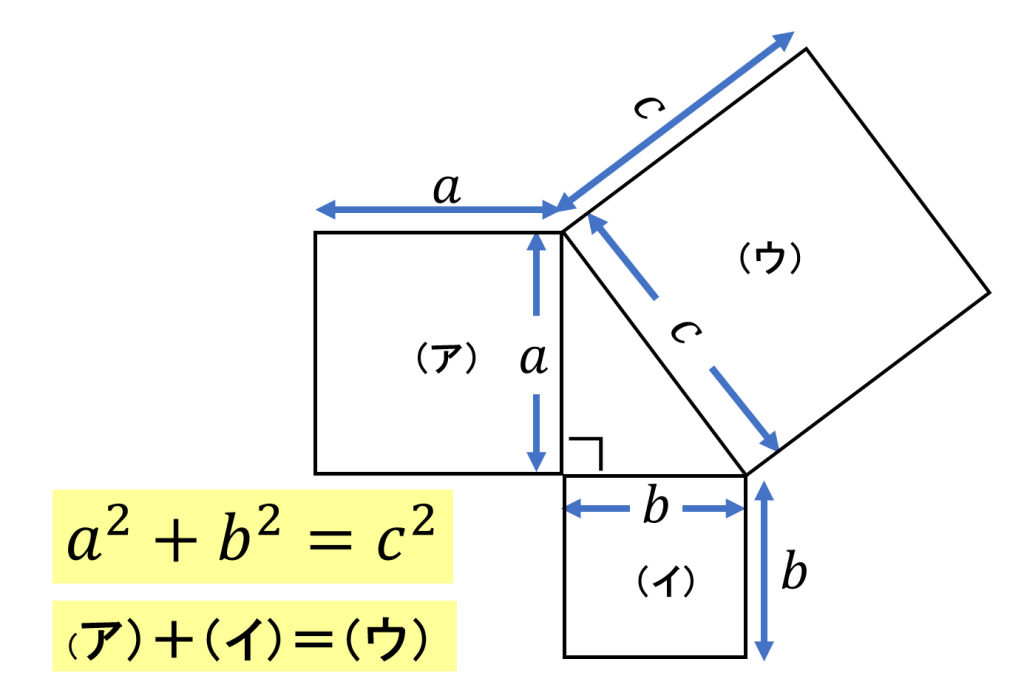
さて、三平方の定理で最もおなじみなのは、おそらく次の図でしょう。
直角三角形の3辺それぞれに正方形を描き、その面積の関係から「斜辺を1辺とする正方形の面積は、他の2辺をそれぞれ1辺とする正方形の面積の和に等しい」というものです。

そして、具体的な長さとしては「3・4・5」の直角三角形が有名です。そのほかには、「5・12・13」もあります。

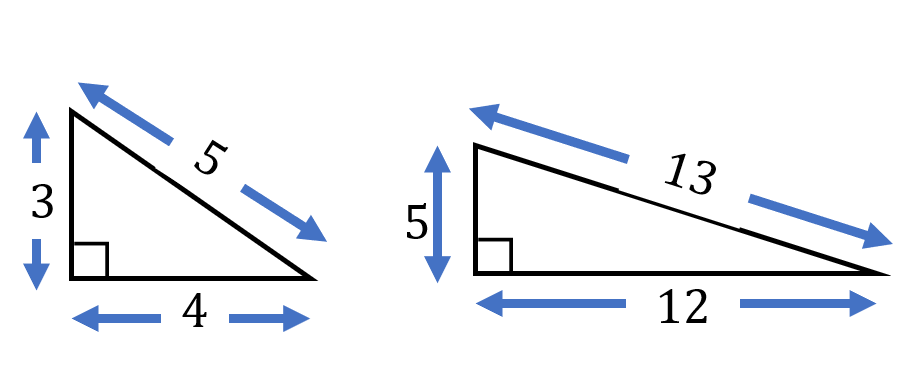
今回は特にこの図をよく覚えていてください。

直角三角形、どこに隠れているかな？

それでは、問題を出します。

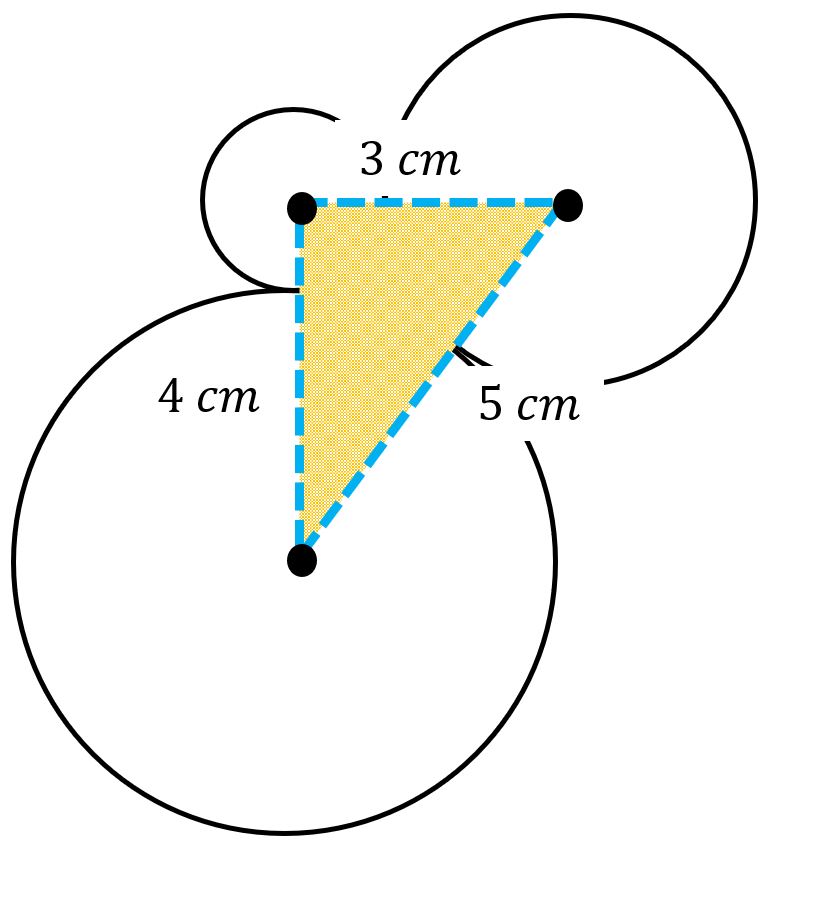
【問題1】　半径1 cm、2 cm、3 cmの円が互いに外接しています。3つの円の中心を結んでできる三角形の面積は何cm²ですか。

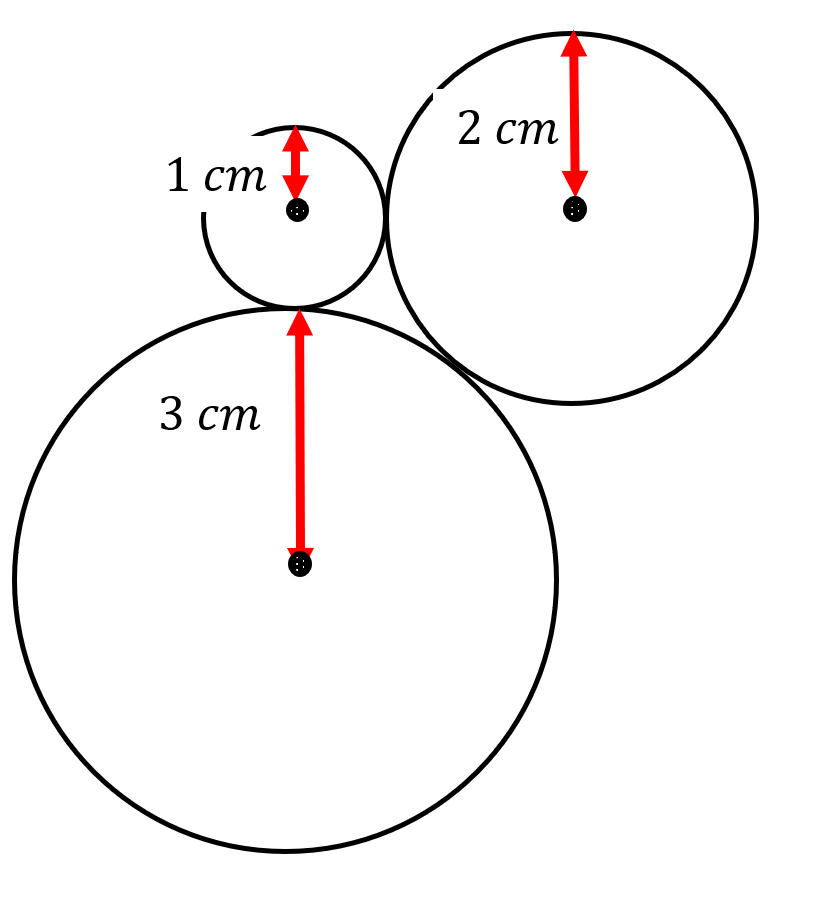
［解答1］　互いに外接しているため、円の中心間の距離はそれぞれの半径の和になります。
したがって、三角形の三辺の長さは以下の通りです：

• 半径1 cmと2 cmの円の中心間：1 + 2 = 3 cm
• 半径2 cmと3 cmの円の中心間：2 + 3 = 5 cm
• 半径1 cmと3 cmの円の中心間：1 + 3 = 4 cm

つまり、三辺は 3 cm、4 cm、5 cm の三角形。これは、図でお見せした直角三角形です。

ですから、面積は、$\frac{1}{2}×3×4 = 6$ cm² 　です。

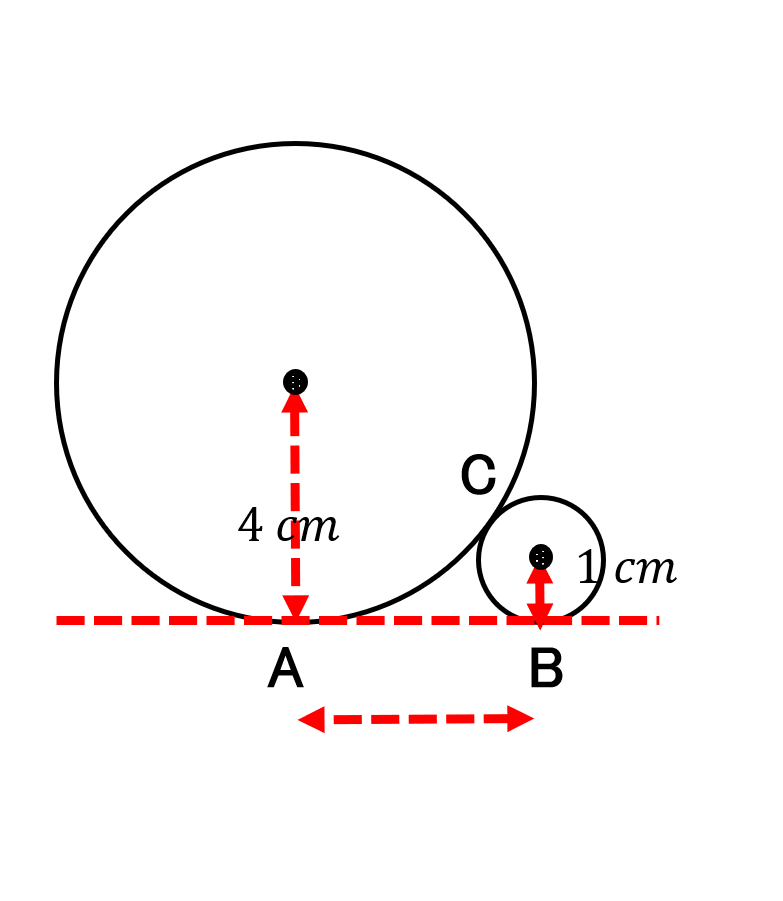
【問題2】　半径4 cmの大きな円と半径1 cmの小さな円が、点Cで外接しています。
それぞれの円は、点A・点Bで共通の接線Lに接しています。
このとき、点Aと点Bを結んだ線分ABの長さは何cmですか？

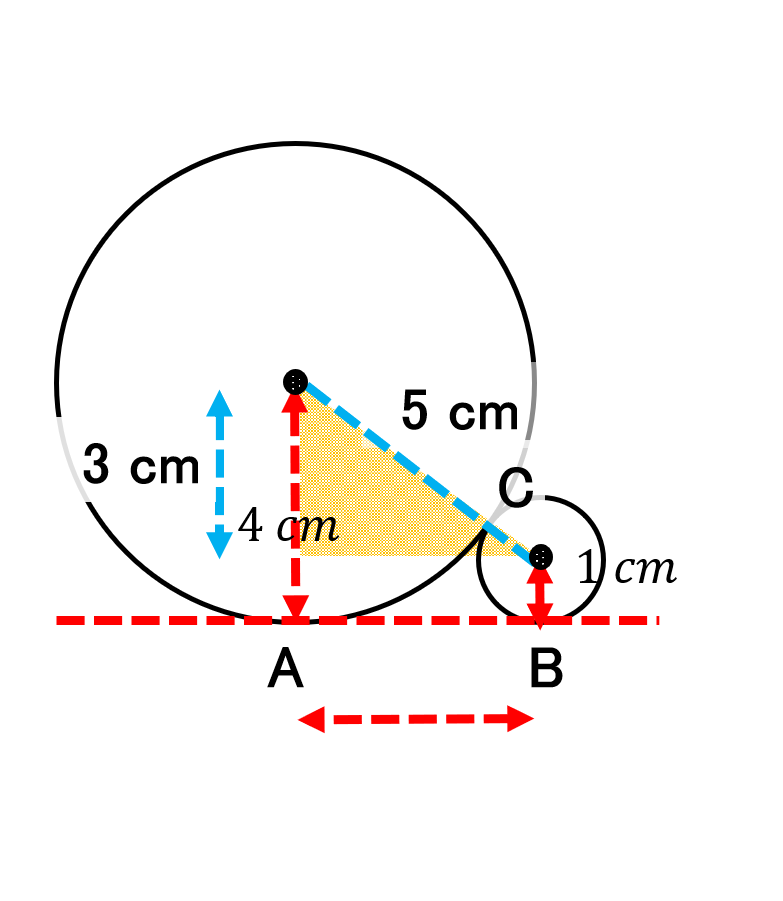
［解答2］　図のように円の中心同士を結ぶ線と、共通接線Lを利用して図を考えましょう。

• 大きな円の半径は4cm、小さな円の半径は1cmなので、中心同士を結ぶ線の長さは 4 + 1 = 5 cm。
• 両方の円の中心から接点A・Bに下ろした垂線の長さは、それぞれ 4 cm と 1 cm。
• これにより、直角三角形ができ、その三辺は 3 ㎝、4 ㎝、5 ㎝。

またしても、3辺が3 ㎝、4 ㎝、5 ㎝の三角形が浮かび上がってきました。答えは4 ㎝です。

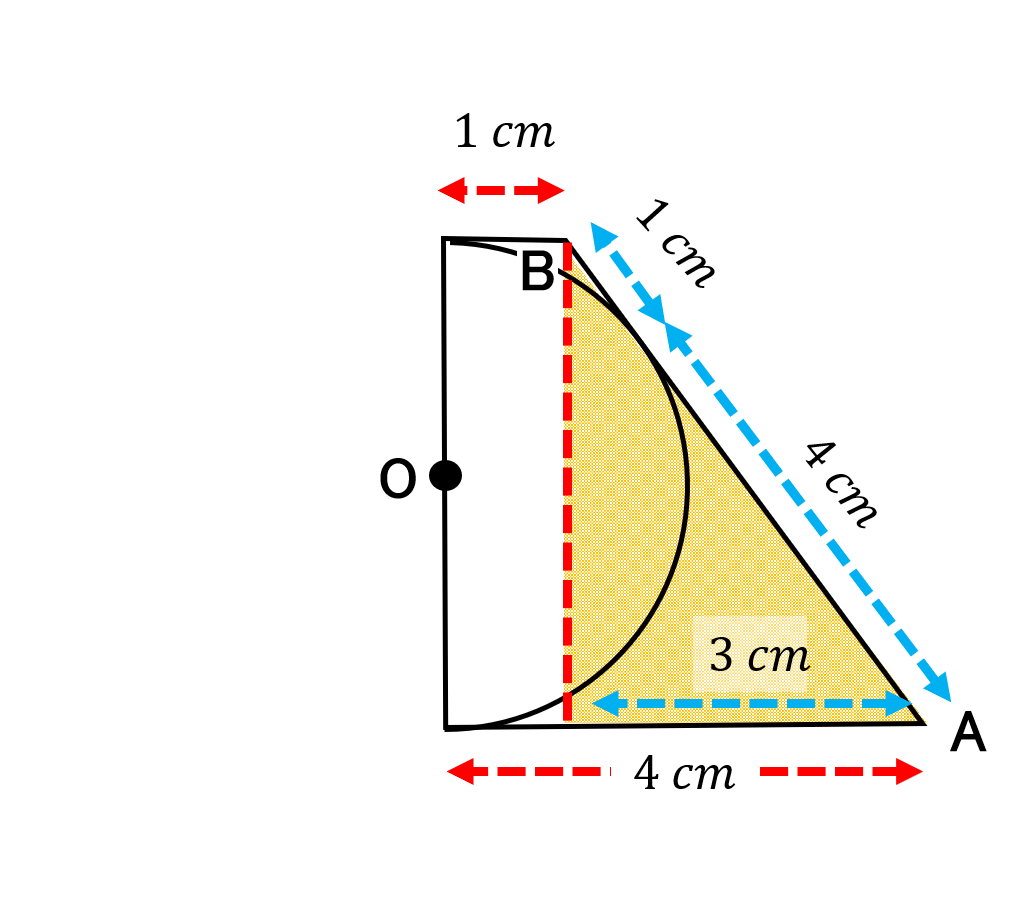
【問題3】　台形と半円が図のように接しています。円の直径は何 ㎝ ですか。

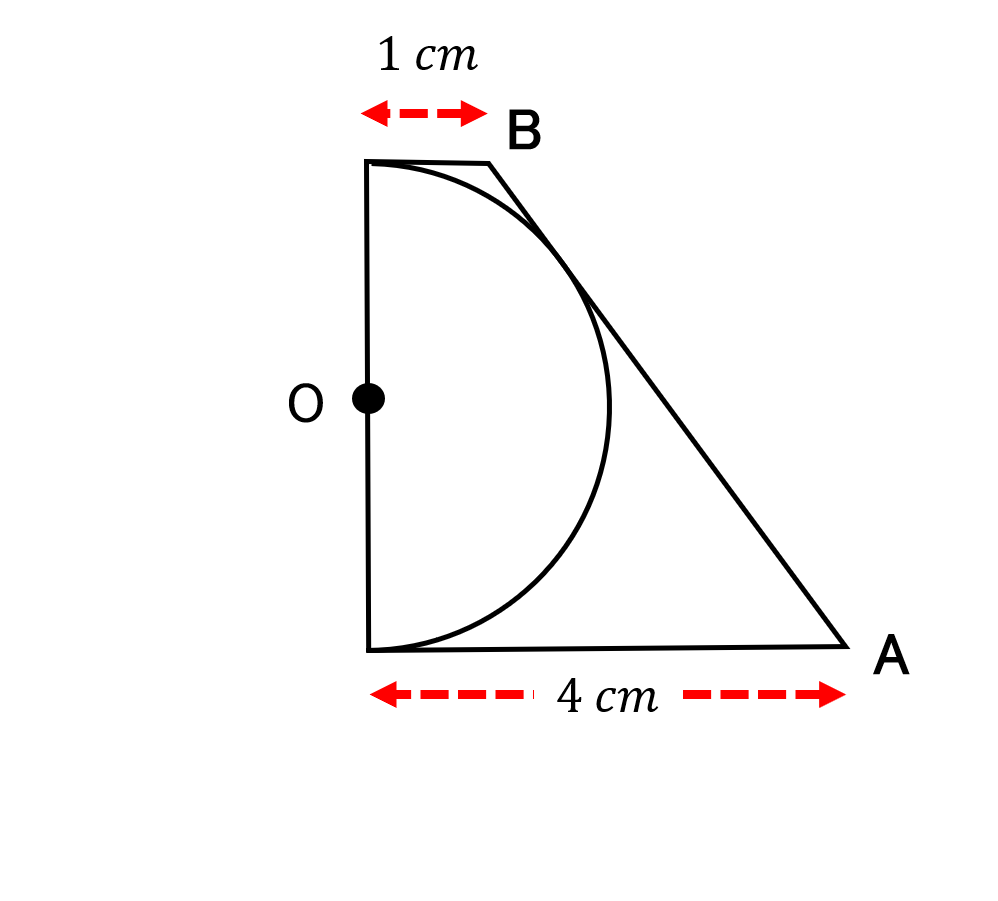
［解答3］　円の外にある1点から円に向かって接線を引くと、通常2本の接線を引くことができます。そして、この2本の接線の円の外の点から接点までの長さは、必ず等しくなります。

なぜそうなるのでしょうか？

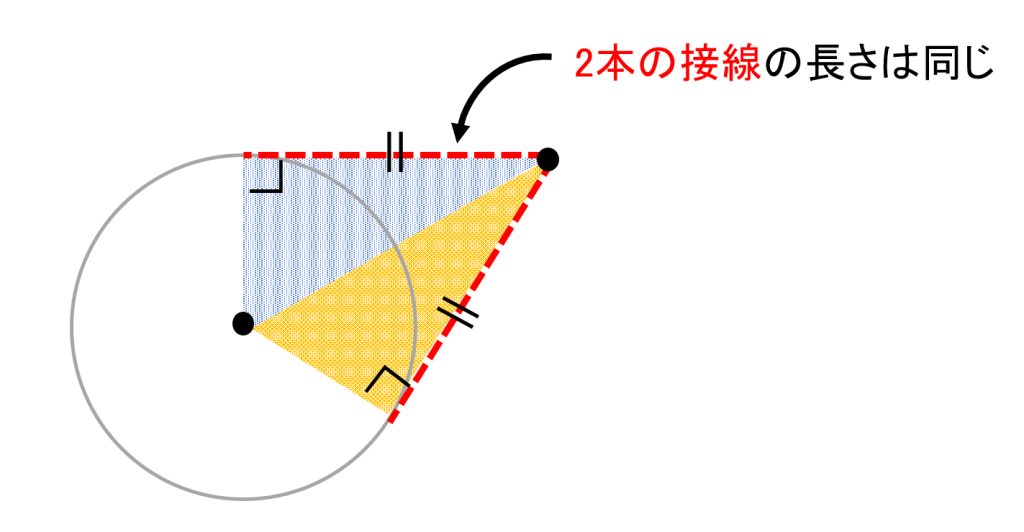
それは、できあがる2つの三角形が合同になるからです。
具体的には、円の中心と接点を結ぶ線（半径）は接線と直角に交わるため、どちらの三角形も直角三角形になります。また、共通の辺（外の点から円の中心への線分）を持ち、半径の長さも等しいため、斜辺と他の１辺が等しい合同条件（直角三角形の合同条件）が成立するのです。

したがって、図の中に長さを書き加えると、これまた、三辺が3 ㎝、4 ㎝、5 ㎝の三角形が浮かび上がってきます。答えは4 ㎝です。

おわりに

いかがでしたか？
今回は、ほとんど計算をせずに楽しめる、三平方の定理に関する問題をご紹介しました。すべて「3・4・5」の比で直角三角形ができるという基本的な知識と、その三角形がどこに隠れているかに気づけば、すぐに解ける問題ばかりだったと思います。

お友達にパズルとして出すときには、「5・12・13」の三辺を使った直角三角形のパターンにすると、少し難易度が上がって盛り上がるかもしれません。

実は、三平方の定理の世界はとても奥深く、証明方法だけでも数百種類あるといわれています。
有名なピタゴラスをはじめ、アインシュタインやガウスといった数学者たちも、それぞれ独自の証明を残しています。
さらには、アメリカの第20代大統領ジェームズ・ガーフィールドまでもが、ユニークな方法でこの定理を証明したという逸話もあります。

三平方の定理は、面積の関係から説明できることも多く、それを応用した面白い問題もたくさん存在します。
次回は、そんな「面積」に注目した三平方の問題を取り上げる予定です。どうぞお楽しみに！

（文責：みうら）

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

文系オトナですが、今から数学を楽しめますか？ [ math channel ] 価格：1,760円（税込、送料無料) (2025/7/3時点) 楽天で購入

数学博識王みうらの人気記事　こちらもどうぞ！