こんにちは、みうらです。
前回は「缶ジュースの問題」をテーマにその解法と応用をわかりやすく紹介しました。
今回は、この缶ジュースの問題を「文字式を交えて一般化」して紹介します!
前回の復習から
今回は、前回ご紹介した内容を少しレベルアップして、一般化してみましょう。
その際に使うのが、ちょっと新しい記号――ガウス記号 [ ] です。
この記号[X]は、「X を超えない最大の整数」を表します。たとえば、
[3]=3、 [4.8]=4
といった感じですね。数学的には「床関数」と呼ばれることもありますが、今回はこの[ ]の使い方に慣れてもらえれば大丈夫です。
また、この記事の内容をしっかり理解するためには、不等式(大小関係)の知識もあるとよりスムーズです。
「すこし難しそう…」と思った方も、前回の記事を読み返しながら進めれば、きっと大丈夫!
それでは、はじめましょう!
まずは(問題1)の問題の数値を文字に置き換えてみます。
問題1) ジュースをn本買うと、新品のジュース1本をおまけにくれます。M本購入すると、おまけは何本ですか。
問題2) 飲んだ後の空缶をn個持って行くと、新品のジュース1本をおまけにくれます。 M本購入すると、おまけは何本ですか。
問題1) の解答
割り算した商ですから

問題2) の解答
前回、具体的な数で説明した内容を、文字で表現します。
まず缶ジュースの置き場所を、3カ所設けます。場所1,場所2、場所3と名付けます。
場所1:缶ジュースを1本置きます。
場所2:缶ジュース (n-1) 本を一束にしたものをできる限り束にして置きます。束には、左からB1,B2,…と名前を付けます。束は

できます。
場所3:残りの缶ジュースを置きます。0本から(n-2)本の場合があります。本数をRとすると
0≦R≦n-2
場所1、2,3に分けて配置した缶ジュースの状態を下図に示します。
場所1にある缶ジュースと場所2にある缶ジュース1束を組み合わせると 缶ジュース n 本の集まりができ、それらを飲み切ると、1本おまけがもらえます。このおまけを場所1に置きます。この模様を下図に示します。場所2にある束から選ぶ1束は任意でよいのですが、この図では場所1と場所2中のB1を組み合わせたものを示しています。

以下同様に、場所1の1缶と場所2の1束を組み合わせて、おまけの交換を繰り返します。束の数(※)回繰り返した後は、場所1に1本と場所3にR本残ります。残った缶は、合わせても、1+R ≦ 1+(n-2)=(n-1) 、つまり(n-1)本以下です。従って、空き缶にしたところで、おまけがもらえる個数にならないので、これで終わりです。結局おまけは、交換した回数と同じで

もらったことになります。
適用例
空缶を4個持って行くと、新品のジュース1本をおまけにくれるとして、この公式を、1000本の場合と10000本の場合のおまけの本数を計算してみましょう。
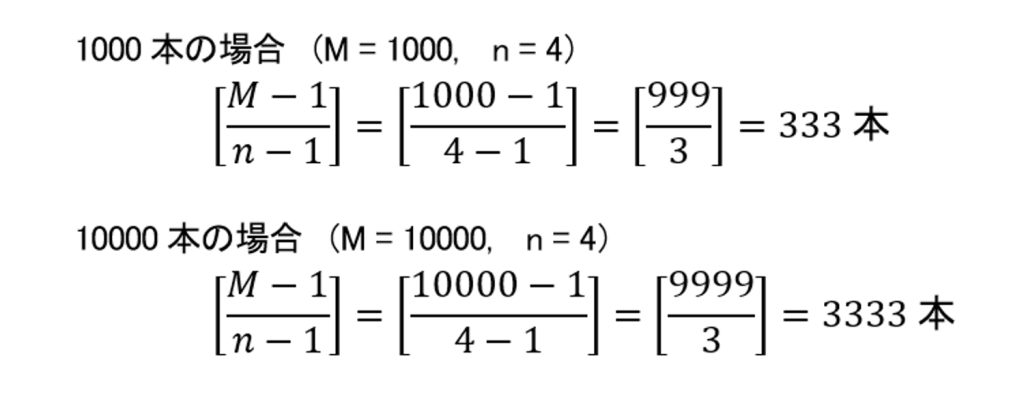
簡単に計算できましたね。前回の記事に出てきた問題3は、公式※と※※を組合わせると解けます。
さらなる拡張
『M本の缶があります。n本の空き缶を持っていくと、h本のおまけをくれます。このとき、おまけでもらえる缶の本数はいくつでしょうか? ただし、h<n とします。』
このようなサービスは現実には考えにくいですが、架空の設定ということでご容赦ください。
問題2の求め方を考えると以下の式が得られます。

例えば、8本あって、3本空缶を持っていくと2本おまけをもらえる場合は、おまけで
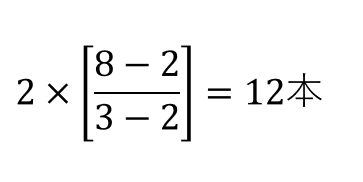
飲めることになります。8本あれば、20本(=8+12)飲めるなんて素晴らしいですね!
おまけ問題
今回の記事を理解していれば、次のような問題にも簡単に取り組めるはずです。
問題4) B商店(空缶4本持ってきたら、1本無料で差し上げるお店)で999本飲むには、何本購入すればよいでしょうか?
問題4) の解答
M本買うと999本飲めるとすると、以下の式がなりたちます。
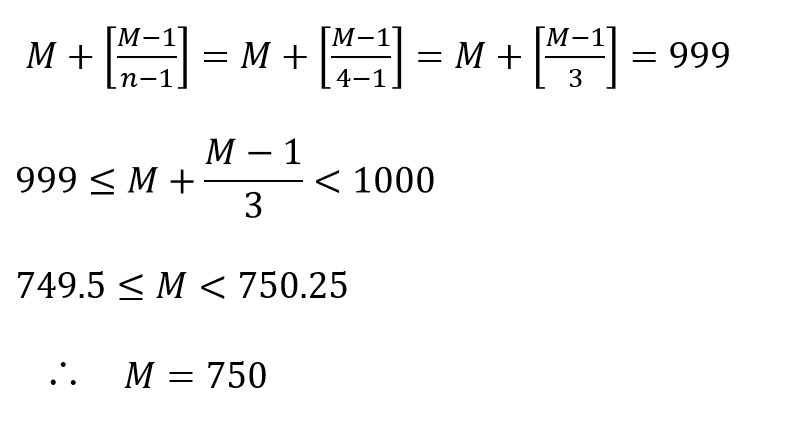
不等式の扱いがちょっと難しいかもしれませんが、こういう風にも活かすことができてしまうのです。
おわりに
いかがでしたか?
今回は、前回(その1)で扱った問題を一般化し、どんなケースにも通用する“公式”としてまとめてみました。これで、この手の「おまけがついてくる系」の問題には、もはや天下無敵です!
ただし、今回は前回と違って、数式がたくさん登場してちょっと大変だったかもしれませんね。もし途中で「ん?」となったら、ぜひ(その1)をもう一度読み返してみてください。やさしい例から入っているので、理解がぐっと進むはずです。
そして今回登場した「ガウス記号」──
これは、高校数学やプログラミングなどでもよく出てくる、とても便利な記号です。今回の問題をきっかけに「ガウス記号、知ってるよ!」と胸を張れるようになってくれたら嬉しいです。
算数や数学には、「具体的な問題から出発して、それを抽象化し、一般的な形にまとめる」という面白さがあります。今回はその一端に触れていただけたなら、この記事を書いたかいがありました。
それでは、また別の問題でお会いしましょう!
(文責:みうら)
著者プロフィール 数学博識王みうら(三浦章)

みうら(三浦 章) math channelマガジン数学博識王
国立市在住。東京工業大学大学院修士課程を修了後、通信キャリヤで30年ほど通信サービスの研究実用化に従事。15年ほど前に、大学教員に転身。情報システム、数学、問題解決フレームワーク等を教えてきました。5年ほど前から地元公民館で月2回程度市民向け数学教室も開催しています。近頃は数学的背景のあるパズルに興味があり、その内容の発信にも関心があります。博士号(工学)、高校教員免許(数学)あり。
■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。
ぜひ、お手にとってご覧ください!