今回は、整数の約数に関する話題です。
約数の個数、約数の和、約数の逆数の和、約数の積を求めてみましょう。
一見単純に思えますが、特に約数の逆数の和や約数の積を求めるのは意外に大変です。
72を例にすると次のようになります。
約数
1,2,3,4,6,8,9,12,18,24,36,72
約数の個数
12個
約数の和
1+2+3+4+6+8+9+12+18+24+36+72=195
約数の逆数の和
$\frac{1}{1}$+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$+$\frac{1}{9}$+$\frac{1}{12}$+$\frac{1}{18}$+$\frac{1}{24}$+$\frac{1}{36}$+$\frac{1}{72}$=$\frac{65}{24}$
約数の積
1×2×3×4×6×8×9×12×18×24×36×72=139,314,069,504
どうですか。特に、約数の逆数の和、約数の積は、計算が面倒なことが実感できますね。
今回は、これらを簡単に求める方法をご紹介します。
求めるための道具は、素因数分解と指数法則です。
聞きなれない言葉かもしれませんが、丁寧に説明します。
なお、計算自体は加減乗除しか使いませんので、ご安心を。
まずは、素因数分解と指数法則の説明から。
1)素因数分解
1と自分自身以外では割り切れない1以外の整数を「素数」といいます。小さい方から、
2,3,5,7,11,……です。
そして、素因数分解とは、整数を素数の積で表すことです。
どんな整数も素数の積で一通りに表される(これには、「算術の基本定理」という名前がついています。名前が大きすぎて内容が浮かんできませんね)ので、素数は物質でいう元素みたいなものです。
ある数を素因数分解するには、小さい素数から順に割っていくことになります。
6と12を素因数分解するとそれぞれ以下のようになります。
6を素因数分解
6=2×3、
12を素因数分解
12=2×2×3
2)指数法則
まず、同じ数を何回か掛けた数の表現法をご紹介します。例えば、2を5回かけること、つまり
2×2×2×2×2 を、$2^{5}$と記します($2^{5}$=32です)。
数の右上に小さく数を書くことで、その数を小さい数の回数だけ掛けることを意味します。この右上に小さく書いた数を指数といいます。慣れないうちは、この書き方に違和感がありますが、慣れると便利です。第一に省スペースになります。
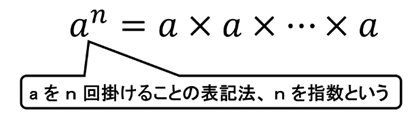
そして、指数法則とは次のようなものです。
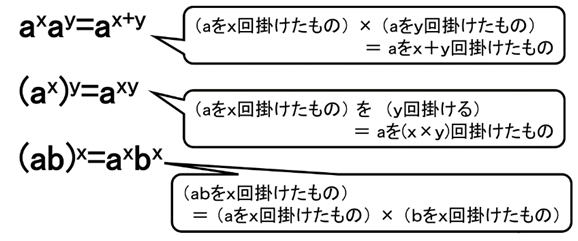
ある数の掛ける回数に注目すると、指数法則は、当たり前といえば、当たり前のことですね。
さて、ここで問題。ある数の指数が0や1の場合、つまり0回掛けるあるいは1回掛けるとはどんなことでしょう。?ですよね。
実は、指数が0や1の場合にも指数法則が成り立つように、
ある数aについて、$a^{0}$=1、$a^{1}$=a、と決めています。
覚えておいてくださいね。
それでは道具立てがそろったところで、いよいよ本題です。
1. 約数と約数の個数
12の約数を考えてみましょう。
12の約数は、1,2,3,4,6,12 の6個です。
1,2,3, ……,12までの数で順に割っていけば求めることが出来ます。
次に30の約数はどうでしょうか。今度は、1,2,3,…… ,30までの数で順に割っていけば求めることが出来ます。1,2,3,5,6,10,15,30の8個です。
でも、こんなことをしていたら、大きな数の場合は手間がかかって、大変です。
そこで、先ほど、ご紹介した素因数分解の出番です。
求めたい数を素因数分解して、素数の積で表してみましょう。
すると、その数の約数は、素因数分解した素数たちを組合わせた(掛けた)ものになっているはずです。
このことを系統立てて書くために、図に表してみましょう。12を例にとります。
素因数分解すると、12=$2^{2}$×3ですね。ですから、下図のような図が書けます。
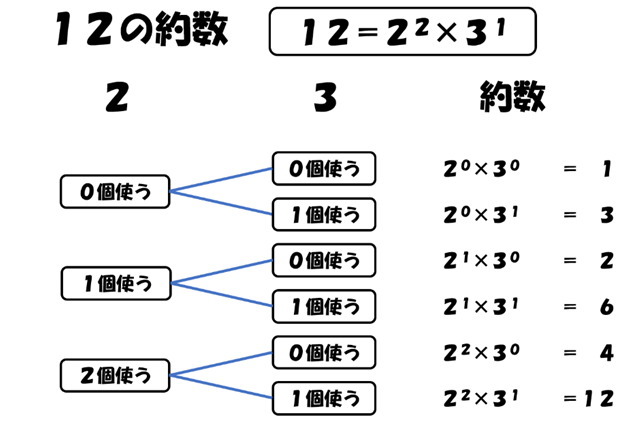
この図を樹形図といいます。
「1、2、3の数字を書いたカードを並べると何通りの数が出来ますか」なんていう問題に使ったことがあるかもしれませんね。樹形図を描くことで漏れなく約数が求められます。約数の個数も6個と分かります。
この樹形図から、約数は、2について、2を使わない場合、2をひとつ使う場合、2を2個使う場合の3通りあることも分かります。3についても、3を使わない場合、3をひとつ使う場合の2通りあることが分かります。ですから、
12の約数の個数=(2を使う場合の数)×(3を使う場合の数)
です。さらに
(2を使う場合の数)=(2の指数)+1
(3を使う場合の数)=(3の指数)+1
です。つまり、
12の約数の個数=(3通り)×(2通り)=(6通り)
と求めることも出来ます。
この様子を絵にしてみました。
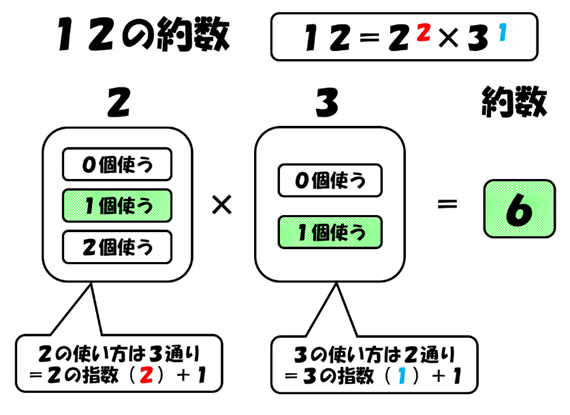
この図を見ていると、約数の個数を求めるには、素因数分解して得られた素数の指数に着目し、それに1を足した数どうしをかければいいことがわかります。
6の場合の樹形図を描いて試してみて下さい。
2. 約数の和
6と12について、樹形図に出てきた約数を上から順に足してみましょう。
足すといっても、片っ端から計算はせずに、共通のかけ算をまとめる(分配法則の逆を行う)ようにして、計算は最後に行うようにします。
すると下のようにきれいな式になります。


これらの例から、計算の方法が浮かんできますね。そうです、数の素因数分解さえできれば、次のような式で求めることが出来ます。
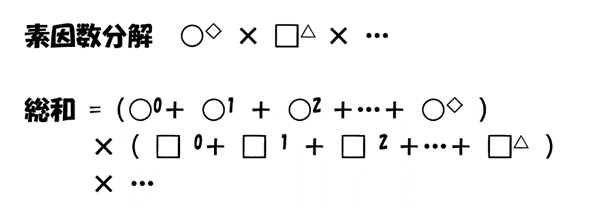
3. 約数の逆数の和
これは、難しそうですが、今までのことが分かっていると、拍子抜けするくらい簡単です。
12の約数の逆数の和を求めてみましょう。次の計算をすることになります。
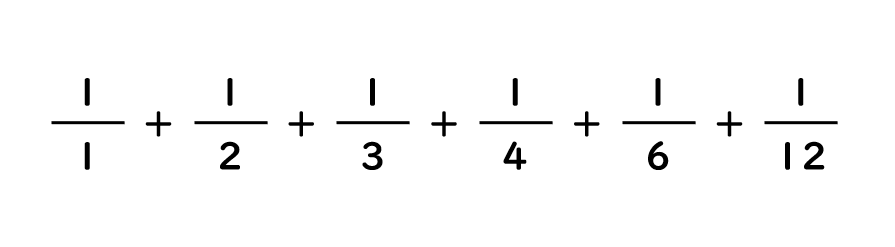
分数を通分します。すると
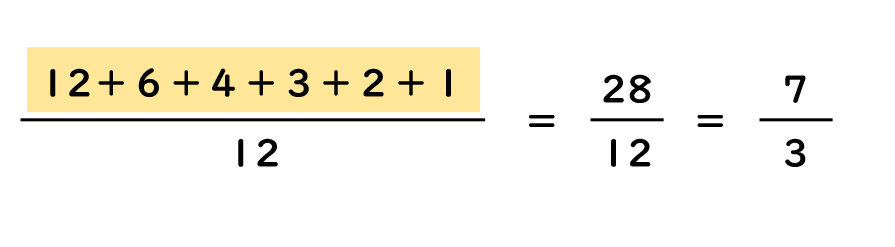
となります。黄色の部分(分子)に見覚えがありませんか。そうですね、分子は約数の和なのです。だから求め方は簡単、先ほど求めた約数の和の公式を使って求めることができます。
公式にすると次のようになりますね。
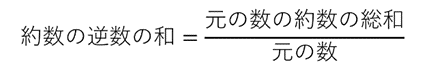
もちろん覚える必要はありませんよ。
4. 約数の積
6の場合で実験してみましょう。
約数の和を求めた際と同じように、約数を書き連ねてみます。図の黄色部分の4個です。
そして、その横に、逆順にしたものを並べます。桃色部分です。
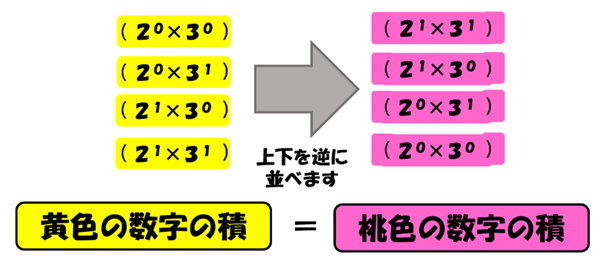
求めたい数は
黄色の数をすべて掛けたもの=桃色の数をすべて掛けたもの
です。
次に横に並んだ約数どうしを掛けます。図の灰色部分が答えです。当たり前ですが、掛けたものは全て元の数(つまり6)になります。
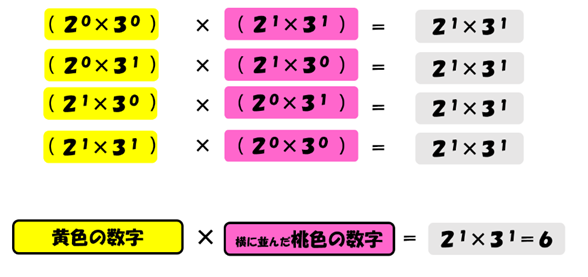
このことから次のことが言えます。
(黄色の数をすべて掛けたもの)×(桃色の数をすべて掛けたもの)=(灰色の数をすべて掛けたもの)
(約数の積)×(約数の積)=(元の数を約数の数だけ掛けたもの)
したがって、
(約数の積)×(約数の積)=(1×3×2×6)×(6×2×3×1)=6×6×6×6=(6を4回掛けたもの)
約数の積を2回掛けたら、6を4回掛けたものになるのですから
(約数の積)=(6を2回掛けたもの)=36
となります。
30の約数の積を求めてみましょう。同じような図を描きます。

これから、
(約数の積)×(約数の積)
= (1×5×3×15×2×10×6×30)×(30×6×10×2×15×3×5×1)
= 30×30×30×30×30×30×30×30
= (30を8回掛けたもの)
ですから
約数の積=30を4回掛けたもの=810,000(81万)
となります。
一般化すれば、Nの約数の個数を▲とすると、
$(Nの約数の積)^{2}$ =$N^{▲}$
となることがわかります。
5 おわりに
如何でしたか。
単に公式を覚えているだけでは、3、4で示した約数の逆数の和や約数の積の求め方は容易に導けません。公式を導く過程、つまり、理論や方法の背後にある原理を理解していることが重要です。
その根本としては、論理的思考力(重複なくもれなく、系統だって物事を考える力)を向上させることが非常に重要です。
なお、紙面の都合上、約数のべき乗(累乗、同じ数を何度もかけ合わせる計算のこと)の和を求める方法は紹介できませんでした。
例えば72でしたら、約数はこの記事の最初に記したように、
1,2,3,4,6,8,9,12,18,24,36,72 の12個
ですから、約数の2乗の和は
$1^{2}$+$2^{2}$+$3^{2}$+$4^{2}$+$6^{2}$+$8^{2}$+$9^{2}$+$12^{2}$+$18^{2}$+$24^{2}$+$36^{2}$+$72^{2}$ (=7735)
となります。
直接求めようと思うと計算が大変です。でも、ご紹介した約数の和の求め方にちょっと工夫することで求められます。紙面を改め、いつの機会にか、ご紹介したいと思います。
今回のお話はこれにてお終いです。
(文責:三浦章)
math channelの数学博識王のみうらがお届けする算数雑学
こちらもおすすめ!
数学博識王のみうらの記事が読めるmath channelの本
『文系オトナですが、今から数学を楽しめますか?』(笠間書院)
詳細:https://amzn.to/49kqbsE

ビジネスや生活から、エンタメや入試問題まで、
中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
文系も理系も、気づいたら、今よりもっと数学好きになっているかも!?