身の回りには、図形がたくさんあります。
その中の1つに、お風呂場や道路のタイルがあります。どんな形をしているでしょうか。
そうですね、通常は正方形のタイルが使われています。他の形のタイルは見かけません。
なぜタイルは主に正方形なのでしょうか。
その理由は、正方形のタイルは平面に隙間なく並べることができるからです。
このタイルのように平面をいくつかの種類の平面図形を用いて、重なることなく、かつ、隙間なく敷き詰めることを「平面充填」といいます。
どんな形のタイルが平面充填できる?
それでは正方形以外に平面充填可能な図形はどんな図形でしょうか。
考えやすくするために、タイルは1種類に、そして、さらに正多角形のタイルに限ってみましょう。
つまり正三角形、正四角形、正五角形、正六角形、正七角形、…、を対象に考えます。
なお、正四角形という表現は普段あまり見かけませんので、これからは、正方形ということにします。
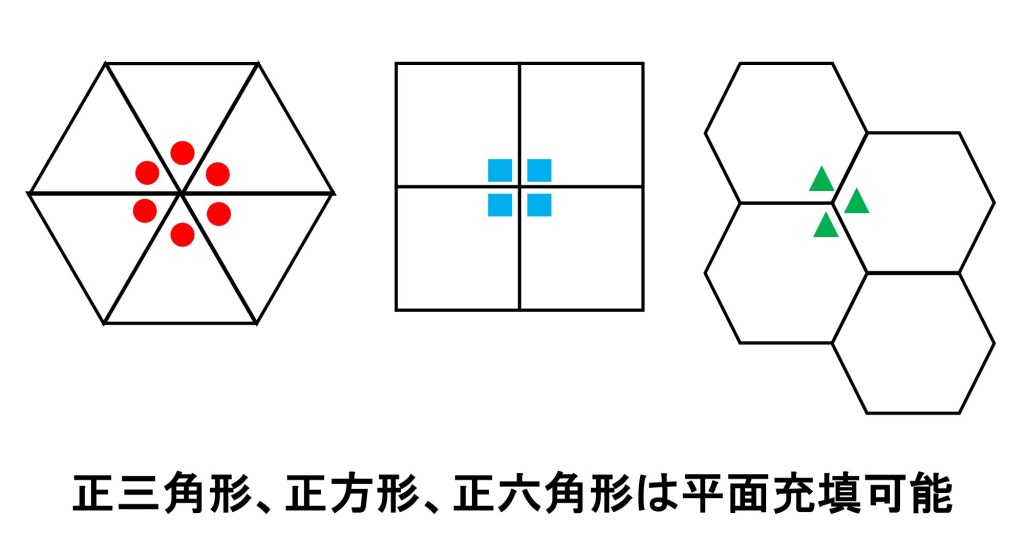
試してみると、正三角形と、正六角形も、きちんと並べられることがすぐにわかります。
正六角形は蜂の巣のような形になります。
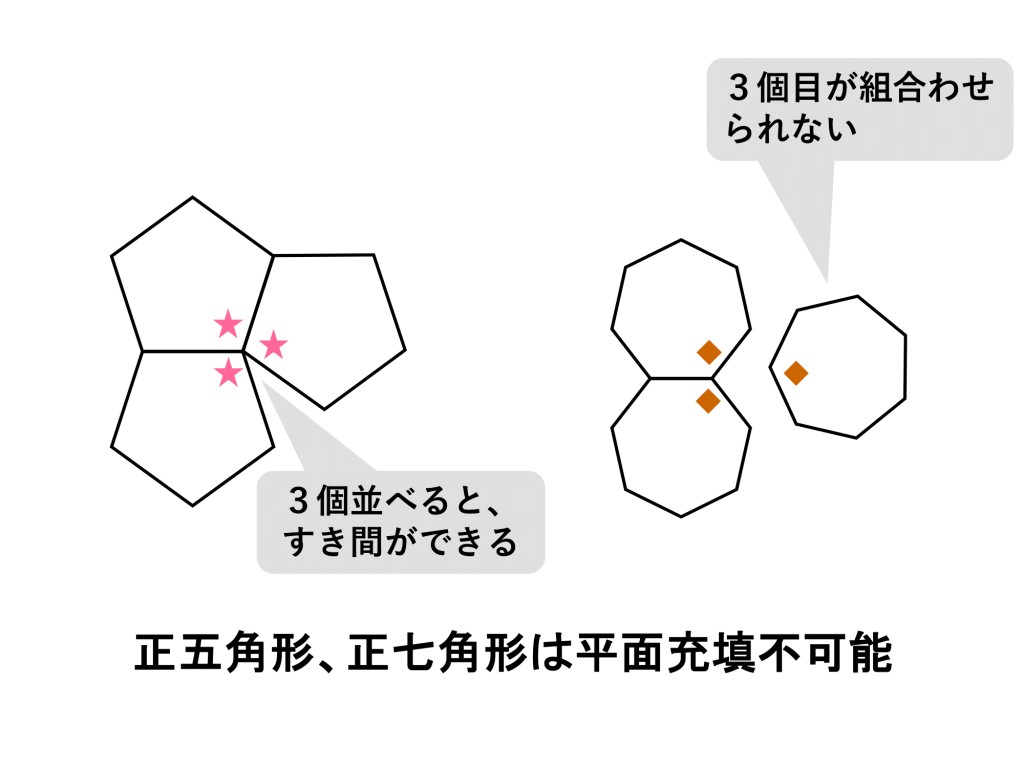
正五角形はうまく並べられません。3個並べたときに少し間があきます。
正七角形ではどうでしょう。これもうまくいきません。
正七角形では頂点のところの角(多角形の隣り合う2辺が多角形の内部に作る角で内角といいます)が大きすぎて1つの頂点の周りに2個しか並べられません。
正七角形以上では平面充填できないワケ
正多角形の内角の大きさは辺の数によって変わります。そして、正多角形が隙間なく並べられるためには、頂点の周りの正多角形の内角の合計が360度になる必要があります。
正三角形、正方形、正六角形は、1つの頂点の周りの内角の合計を360度にできるため、うまくタイルとして並べることができます。しかし、それ以外の正多角形は3個以上並べたときに隙間なく並べることができません。
このことをもう少し、論理的に考えてみましょう。
まず正多角形の内角を求めます。求め方は2通りあります。
(方法1)
n角形を三角形に分けます。(n-2)個の三角形が出来ます。三角形の内角の和は180度ですから、n角形の内角の和は、(180×(n-2))度です。
従って、正n角形の内角の大きさは、次の式で求めることができます。
内角=(180×(n-2)) ÷n=180-360/n 度
(方法2)
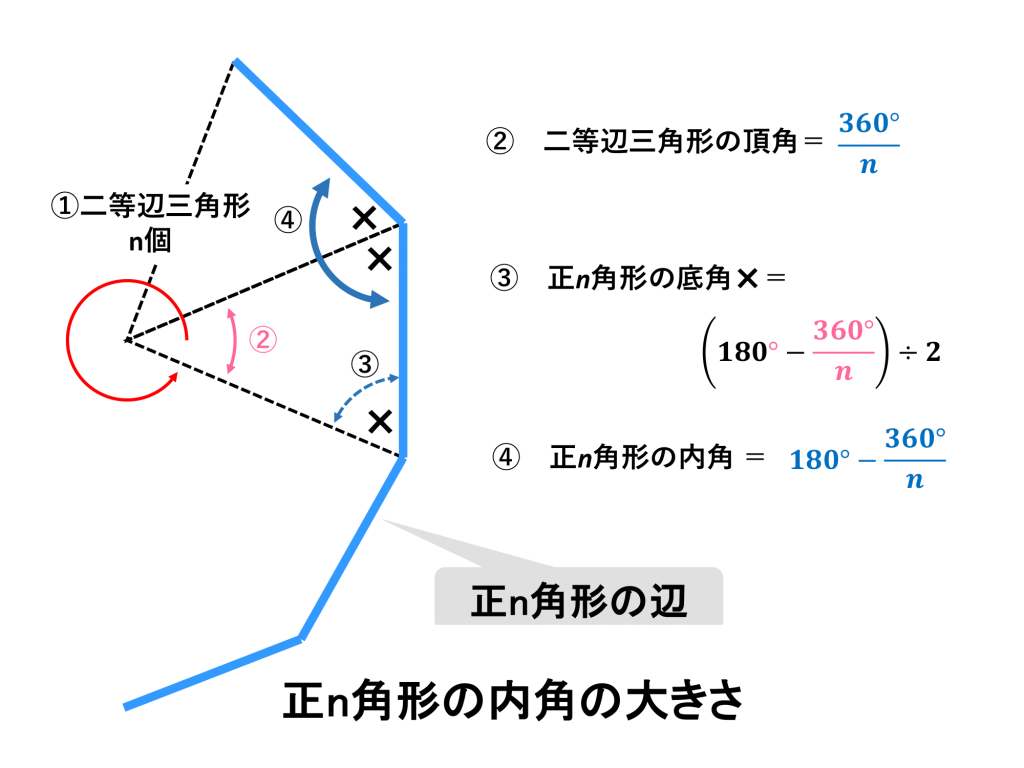
n角形を図のようにn個の二等辺三角形に分けます。頂角は360÷n 度です。底角1つは、(180-360÷n)÷2 度になります。
内角は底角2つ分ですから、
(180-360÷n)÷2×2 度=180-360/n 度
になります。
(方法1)や(方法2)から得られる式を使うことで、内角の大きさが求められます。つまり、
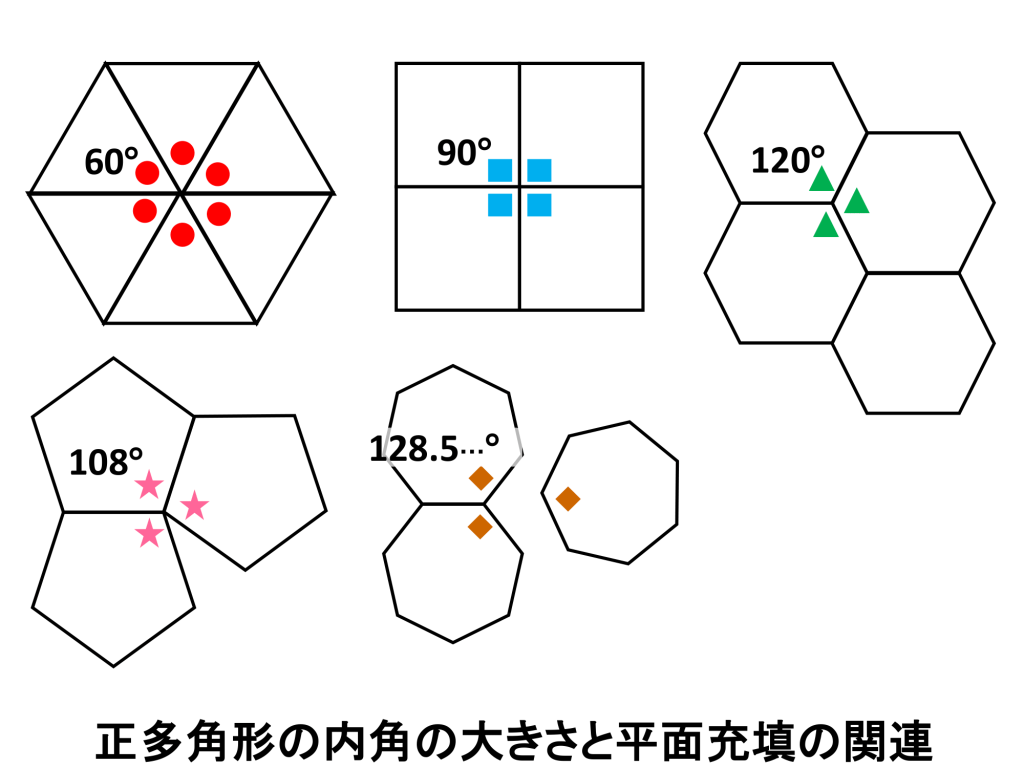
正三角形の場合:内角=(180×(3-2))÷3=60 度
正方形の場合: 内角=(180×(4-2))÷4=90 度
正五角形の場合:内角=(180×(5-2))÷5=108 度
正六角形の場合:内角=(180×(6-2))÷6=120 度
正七角形の場合:内角=(180×(7-2))÷7≒128.5 度
となり、正七角形以上では、1つの頂点の周りに3個以上並べることができません(並べると360度を超えてしまいます)。
以上のことから、
正n角形を1種類用いる場合は、n=3, 4, 6の場合のみ平面充填可能である
ということが分かります。この事実は、既に2500年以上も前に解決されています。
正多角形、複数種類の場合はどうなるのか
こんどは少し難しくなります。特別な場合で試してみましょう。
まずは正三角形と正六角形で平面充填できるでしょうか。
これも先ほどと同じように、頂点に注目して考えると
60度×正三角形の数+120度×正六角形の数=360度
となる正三角形と正六角形の数をもとめれば良い方がわかります。
これを満たすような正三角形と正六角形の組み合わせはあるでしょうか。わかりやすくするために、両辺を60で割ってみましょう。
すると、
正三角形の数+2×正六角形の数=6
となります。
これは、
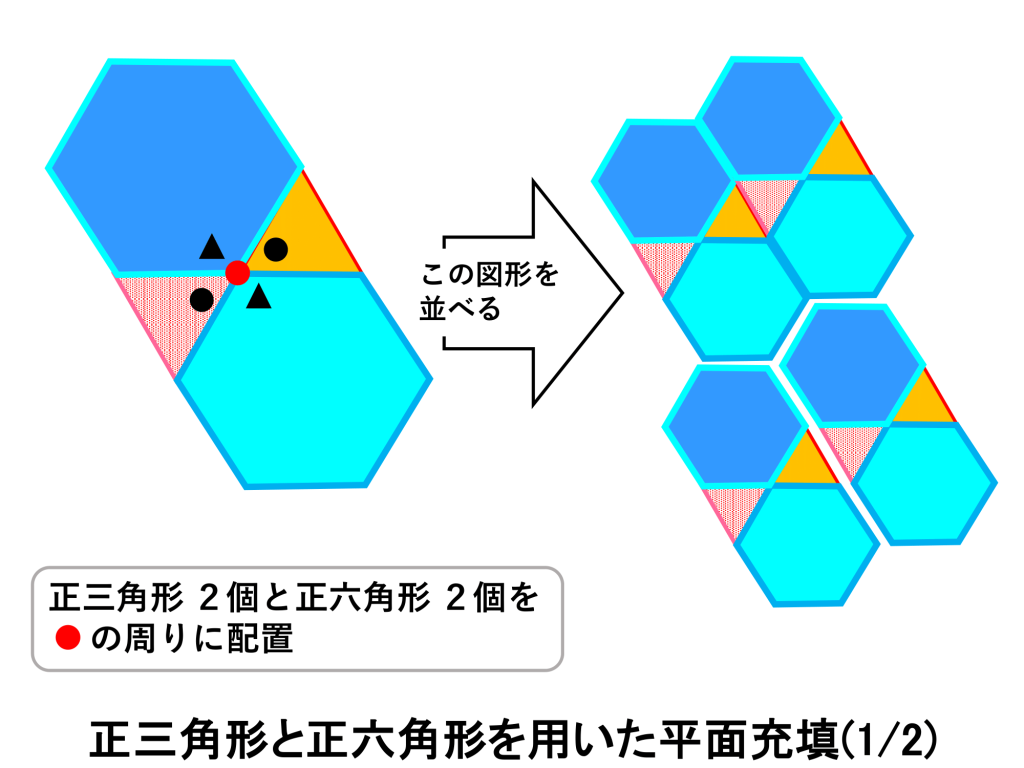
正三角形の数=2、 正六角形の数=2
または、
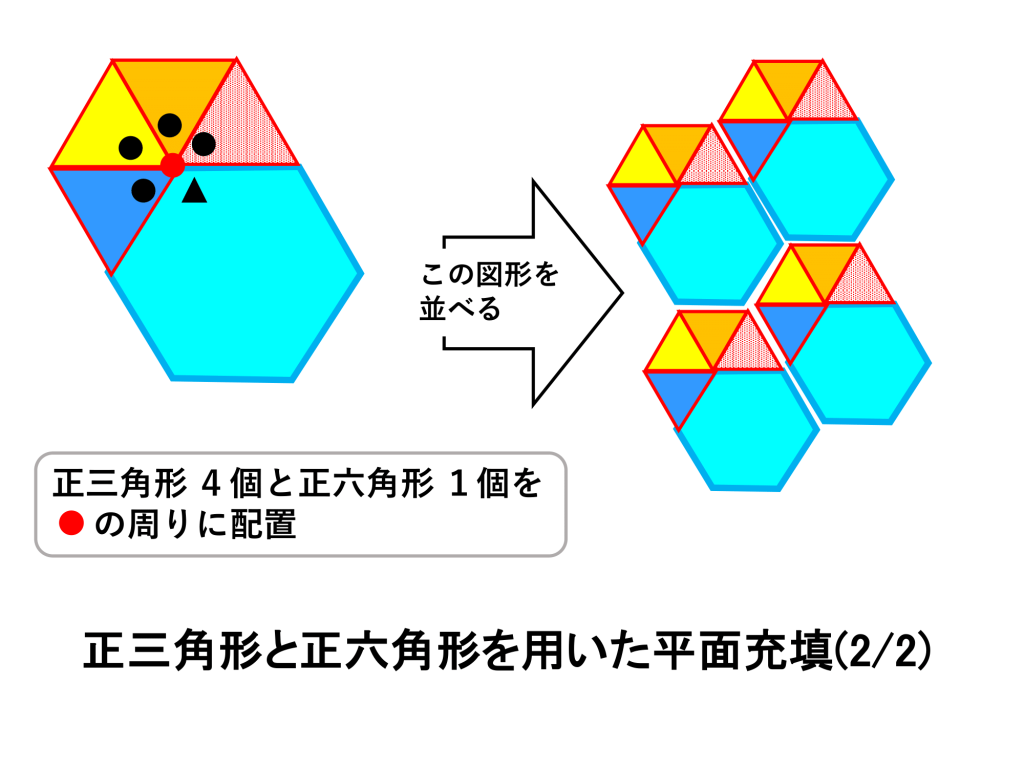
正三角形の数=4、 正六角形の数=1
で成り立つことがわかります。具体的なタイルの並べ方は下図のようになります。
正三角形と正方形で平面充填できるでしょうか。さっきと同じように、
60×正三角形の数+90度×正方形の数=360度
ですから、
2×正三角形の数+3×正方形の=12
を満たす正三角形と正方形の数を求めれば良いことがわかります。
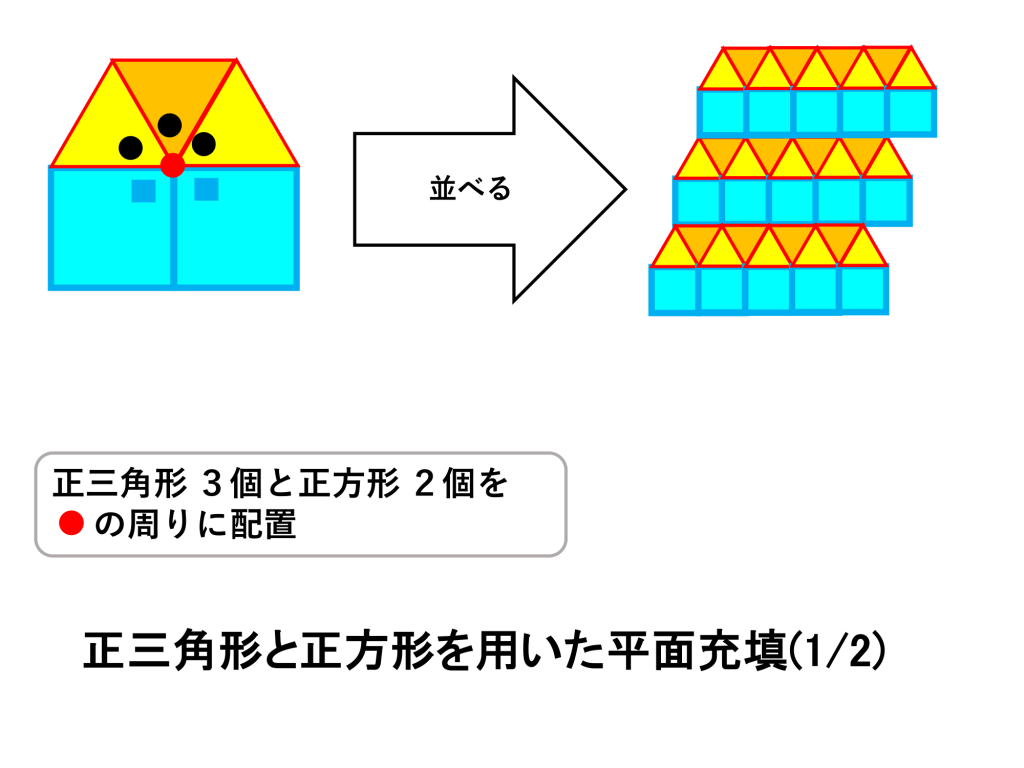
正三角形の数=3、正方形の数=2
この場合は具体的なタイルの並べ方は、下図のように2通りあります。
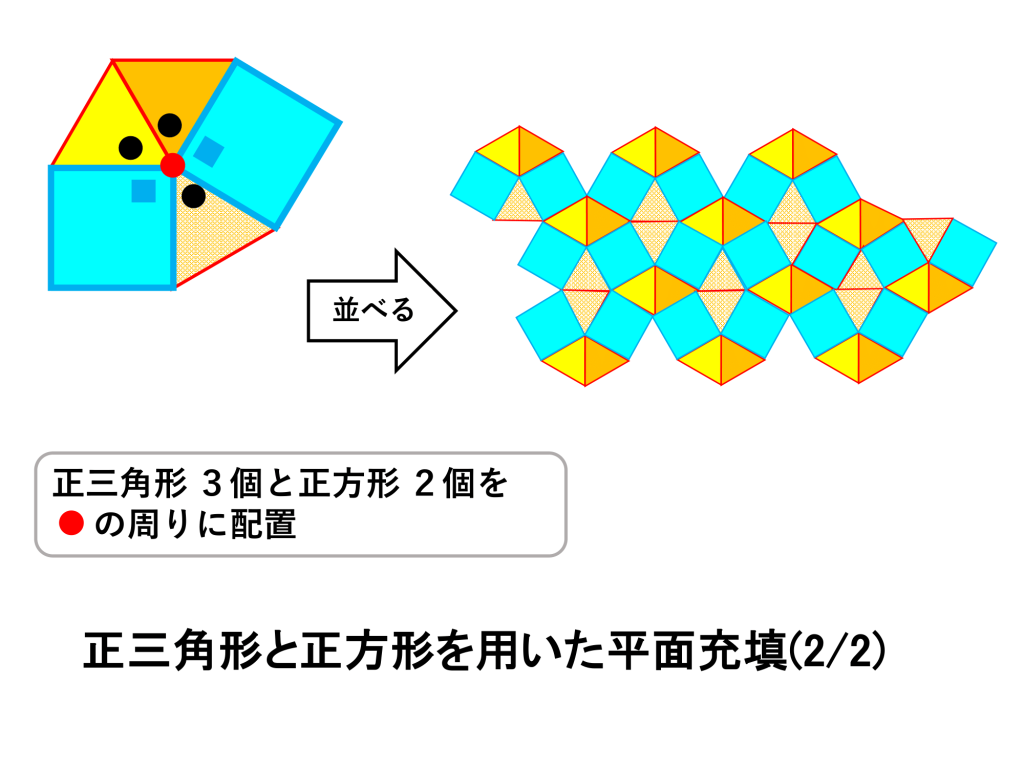
以上、組合せにより平面充填できることをお目にかけましたが、複数種の正多角形で埋め尽くす問題の全パターンを求めるのは多少煩雑です。しかし、驚いたことに、この問題は今から2000年以上前にアルキメデスが解決しています。正多角形の組み合わせにより8通りあり、アルキメデスの平面充填と呼ばれています。
1種類、正多角形以外の場合はどうなるのか?
ますます難易度が上がります。これからのお話は、中にくぼんでいない凸多角形に限ることにします。
まずは、三角形で考えます。紙を切って三角形タイルを作る実験してみましょう。すき間なく並べることが出来ますね。つまり平面充填可能なことが分かります。
なお、よく見ると三角形を2つくっつけた部分は平行四辺形です。つまり、平行四辺形も平面充填可能です。
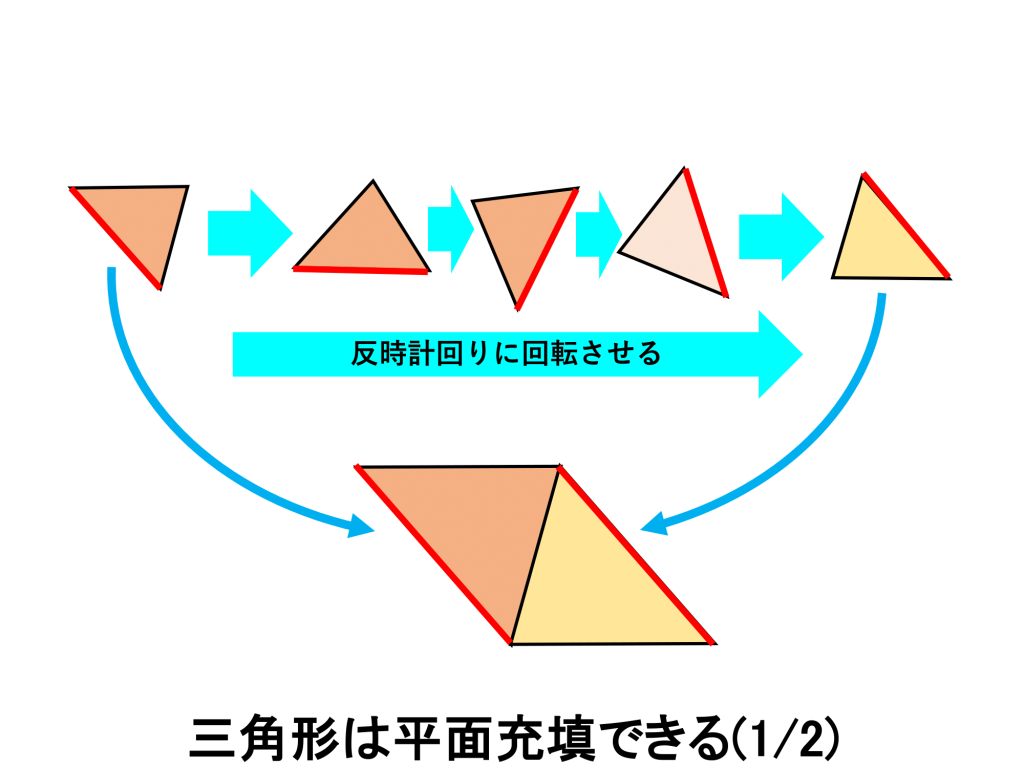
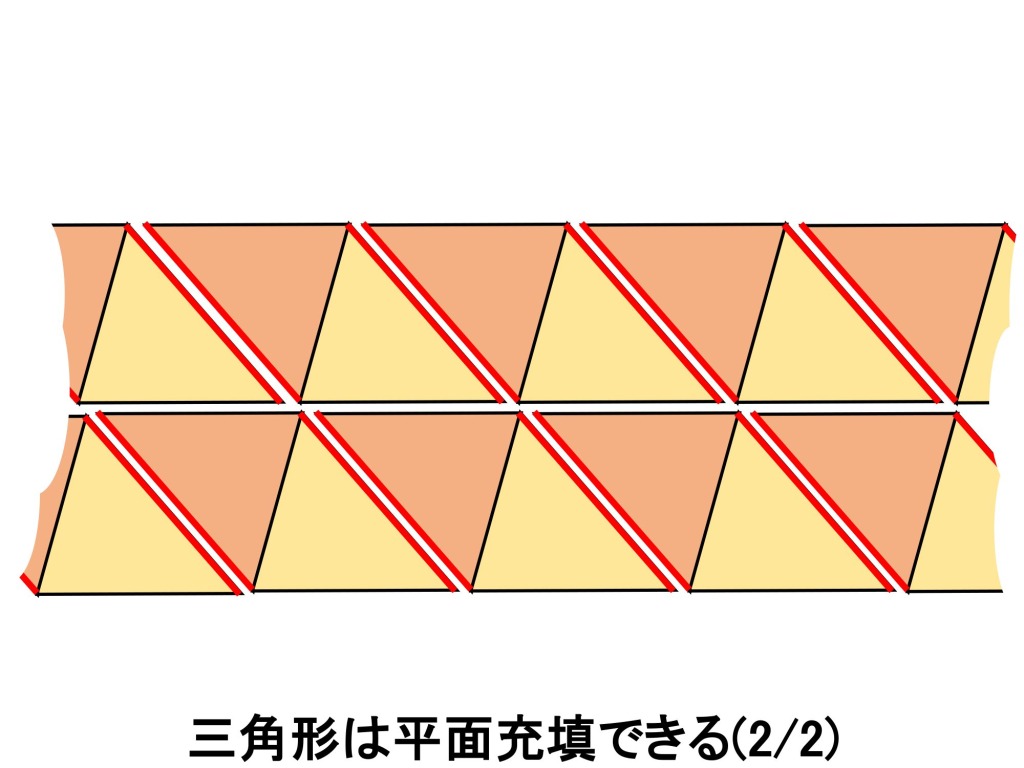
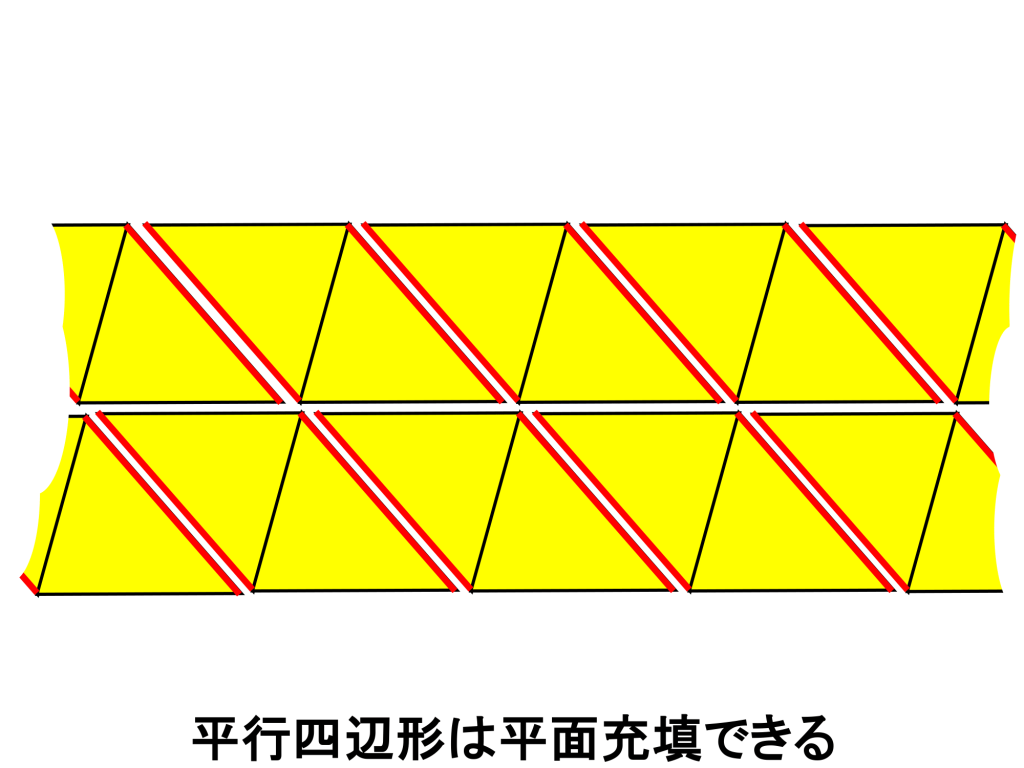
次に一般の四角形を考えてみましょう。
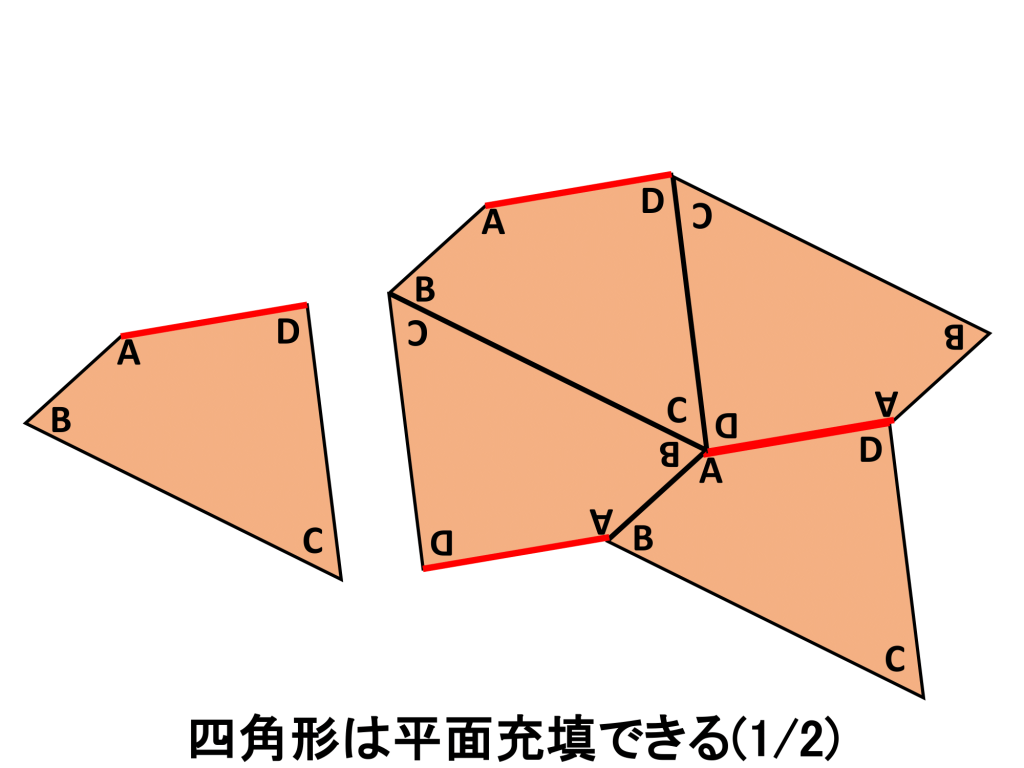
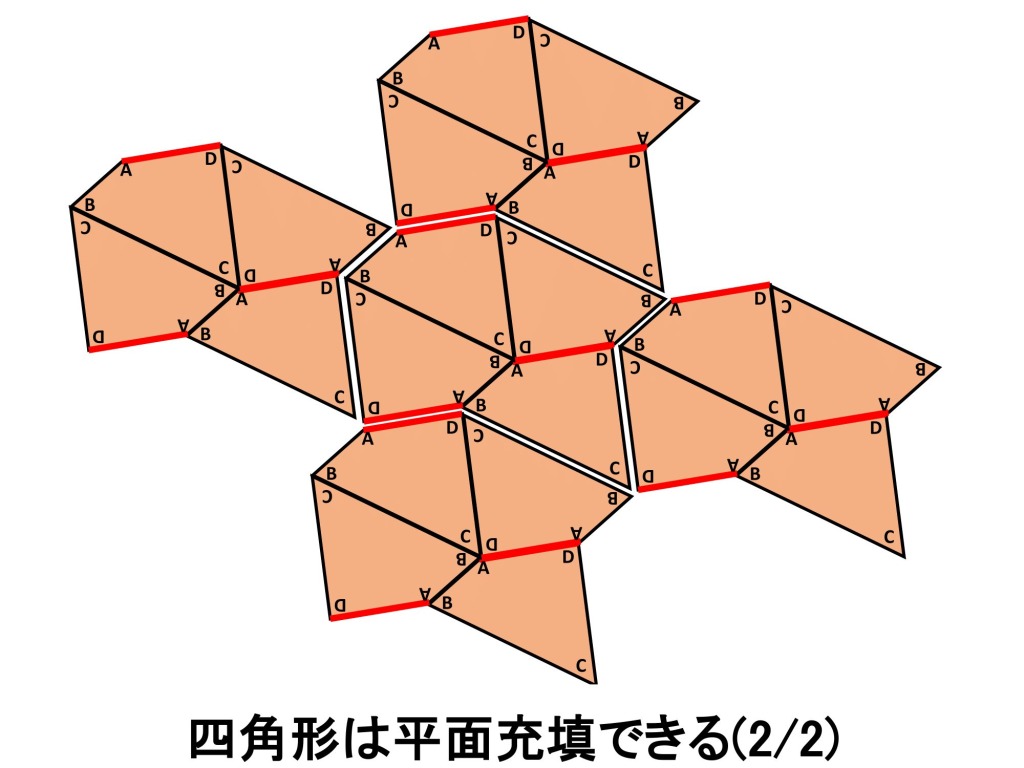
四角形の4つの内角の和は360度ですから、すべての角を点の周りに配置できれば、平面充填できるかもしれません。これも実験してみましょう。
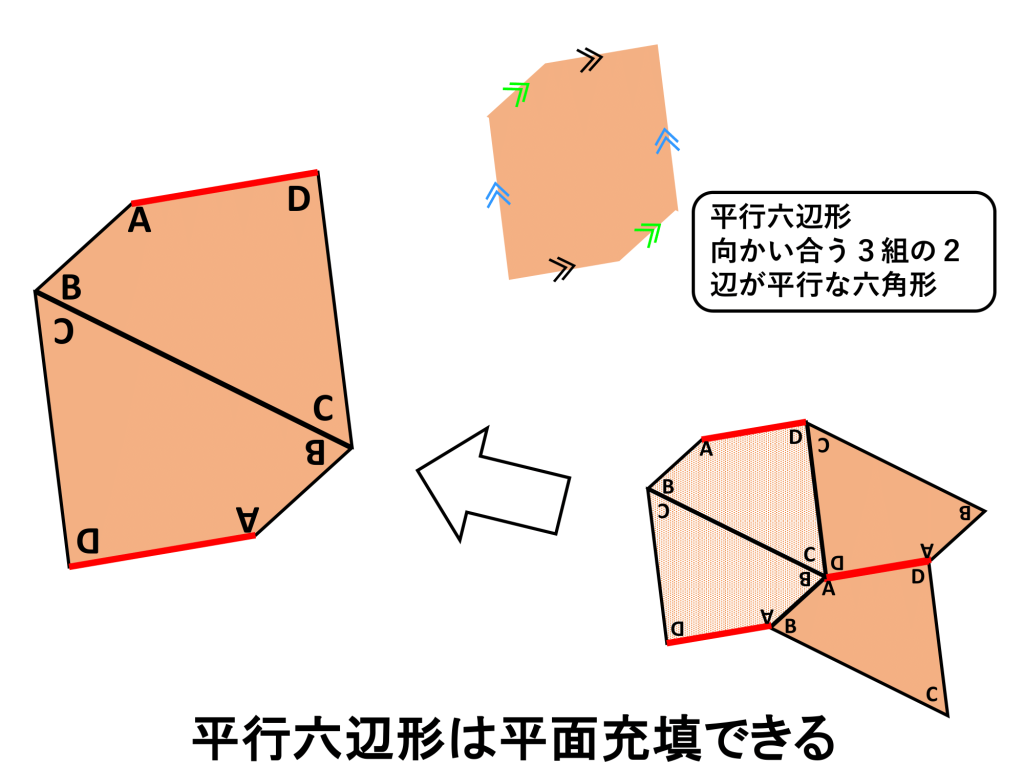
(試行錯誤すると)下図左側のようにして平面充填できることが分かります。そしてさらに、よく見てみると四角形を2個組合わせた六角形の形も平面充填可能なことがわかります。この形は、3組ある向かい合わせの2辺が平行ですので、平行六辺形と呼ばれています。
五角形の場合は15種類の特別な形をしたものが、平面充填可能であることが知られています。16種類以上あるかはまだ分かっていないようです。
最後に七角形以上の場合です。凸七角形以上の場合は平面充填可能でないことが知られています。証明は難しいので、雰囲気をお伝えします。凸七角形がk個で平面を埋め尽くせているとします。
この七角形の内角の和を2通りの方法で計算してみます。
(方法1)平面内にある頂点の数に注目:内角の和=頂点の数×360 度
平面内にある頂点の数を考えます。各頂点には少なくとも3個以上の七角形が集まっていますから、平面内の頂点の数は7×k÷3=7k/3 以下です。従って、頂点のまわりの角度の合計は、7k/3×360 度=840k 度以下です。
(方法2)七角形1つの内角の和に注目:内角の和=七角形の内角の和×七角形の個数 度
七角形の内角の和=180×(7-2)=900 度ですから、七角形の和は、
900 度×k=900k 度です。
(方法1)と(方法2)の結果は明らかに矛盾しています。
つまり七角形では平面を埋め尽くせないことになります。
八角形以上の場合も同じようにして平面充填出来ないことが分かります。
終わりに
平面充填の問題は古くから取り組まれてきた問題で、問題自体は分りやすいのですが、とても奥深い課題があります。平面を曲面に変えて考える、あるいはタイルを三次元にすることなどにより新たな発見もあります。ここで述べた以外に、どのようなことが分かっているのか、いろいろと調べてみてはいかがでしょうか。