○○三角形という名前の三角形、いくつご存知でしょうか。直角三角形、正三角形、二等辺三角形がありますね。鋭角三角形、鈍角三角形なども知っているかもしれません。これらは、その形を表したものですが、形に関わるもの以外に、数を三角形の形に並べたものなどもあります。
今回は、いろいろな○○三角形についてお話しします。
人名がついているものが多いので、人物についても最後にまとめて紹介します。
いくつ知ってる?
まずは、形に関わるもの、次のようなものがあります。
- 「三平方の定理」関連…ピタゴラス三角形 エジプト三角形 ヘロンの三角形
- 「黄金比に関連」関連 …黄金三角形、ケプラー三角形
- 曲線で囲まれたもの …ルーローの三角形
図形ではなく、数を三角形の形に並べたものとしては、
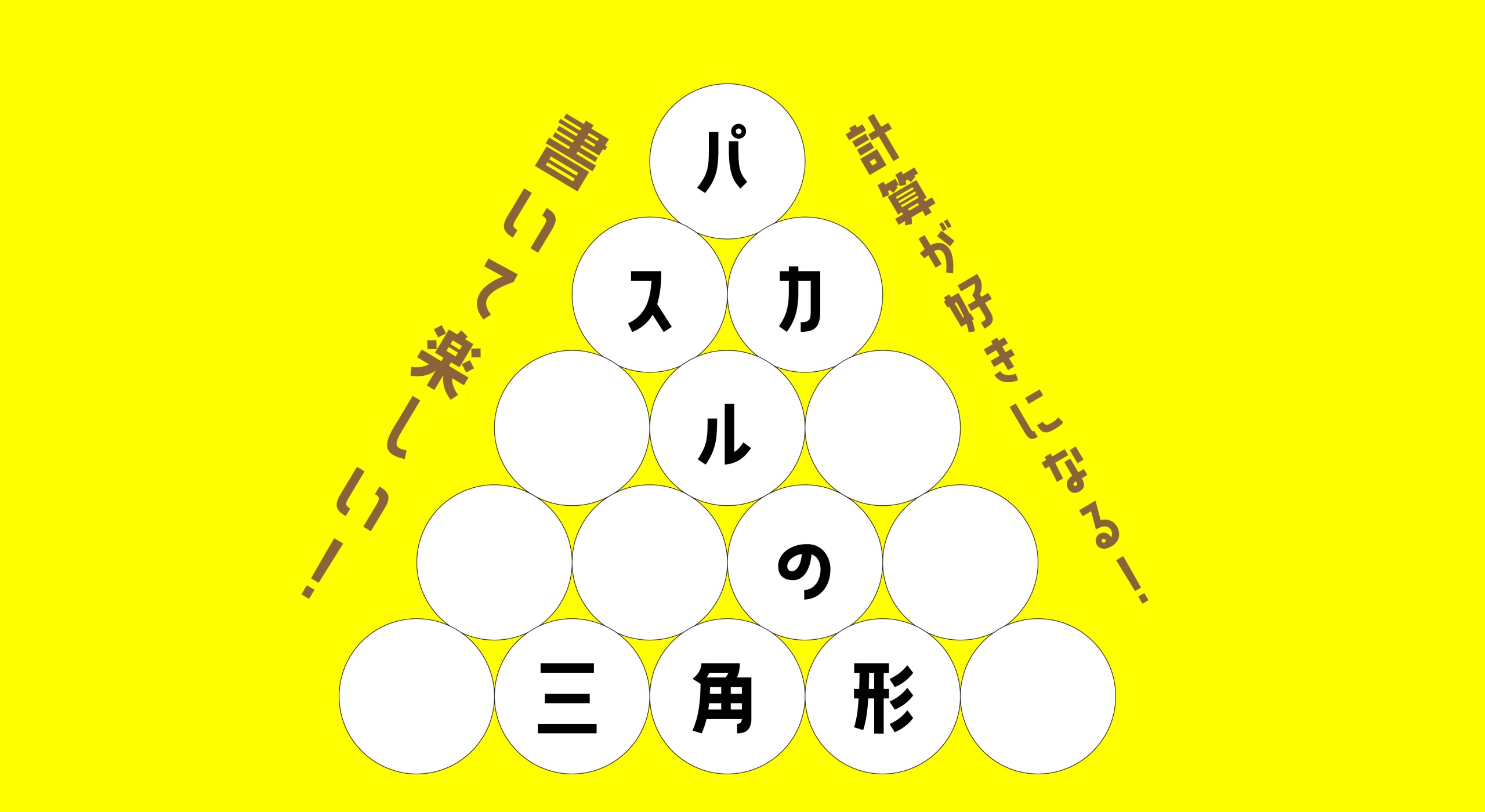
- パスカルの三角形
- フロイドの三角形
- タルタリアの三角形
などがあります。
これらを順にご紹介していきましょう。
まずは「ピタゴラス」三平方の定理について
三平方の定理(ピタゴラスの定理)とは、「直角三角形の直角をはさむ2辺をそれぞれ1辺とする正方形の面積の和は、斜辺を1辺とする正方形の面積に等しい」というものです。
この図を見ると意味がわかるでしょう。
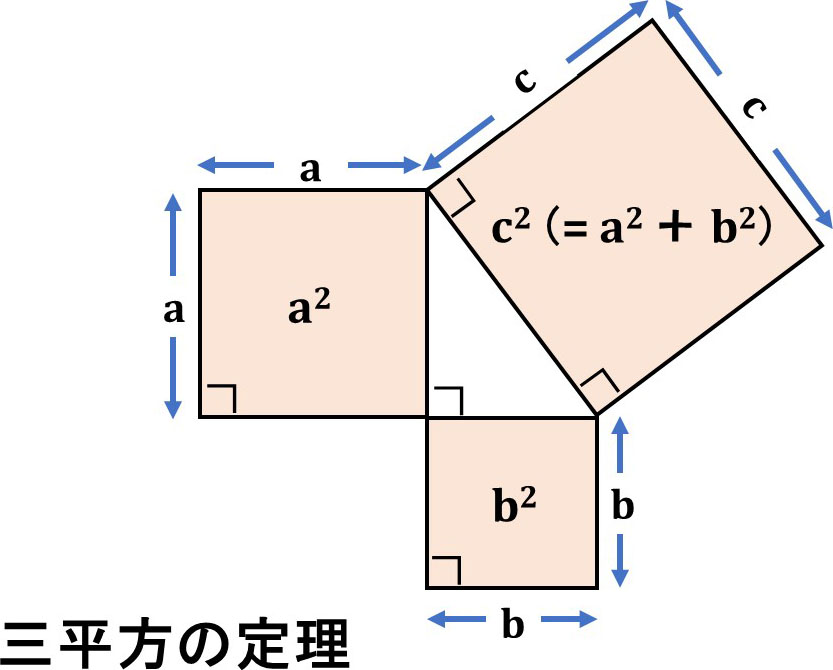
人類にとって古くから、おそらく3000年以上昔から、おなじみのものです。
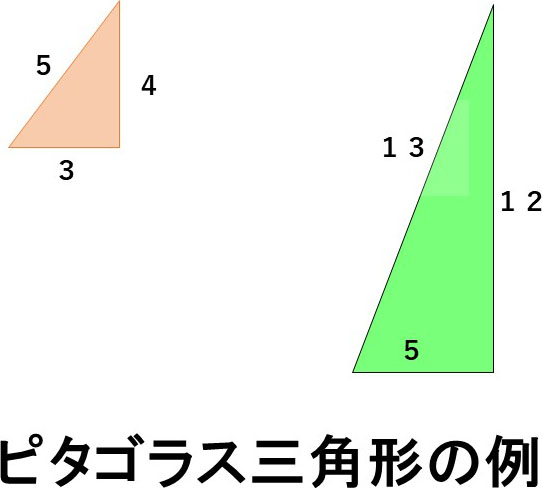
ピタゴラス三角形、エジプト三角形、ヘロンの三角形とは?
ピタゴラス三角形とは直角三角形のうち、3辺の長さが整数比であるものをいいます。
3辺の長さの比が3:4:5の直角三角形が有名です。
ほかにも、5:12:13の三角形などがあります。
長さの比が3:4:5の直角三角形は、古代エジプトでも知られていたということから、エジプト三角形と呼ばれることもあります。
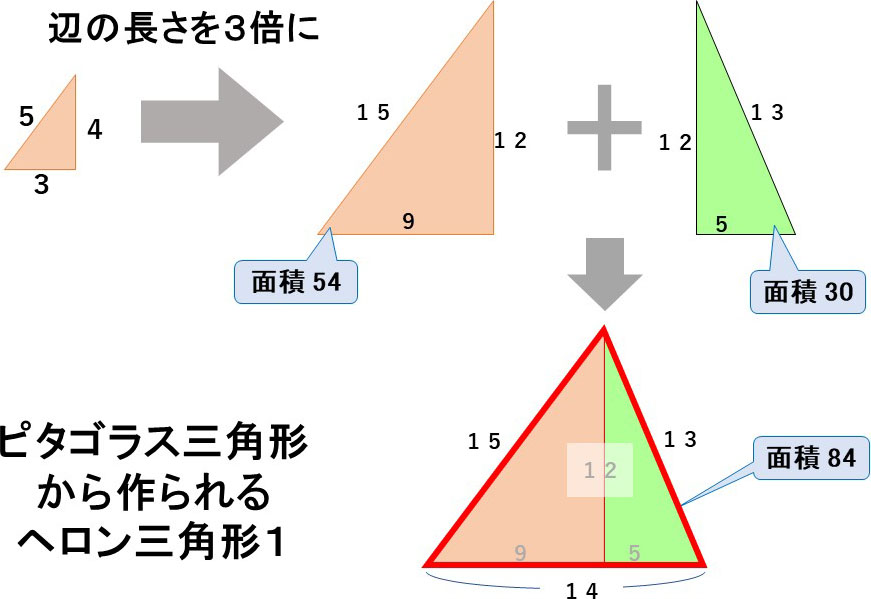
ヘロン三角形は、3辺の長さが整数であり、しかも面積も整数であるような三角形です。
ピタゴラス三角形は面積も整数ですから、2つのピタゴラス三角形の直角をはさむ辺をうまくつなぎ合わせて作った三角形はヘロン三角形になります。
また、重なっている部分を取り去ることでも、ヘロン三角形が作り出せます。
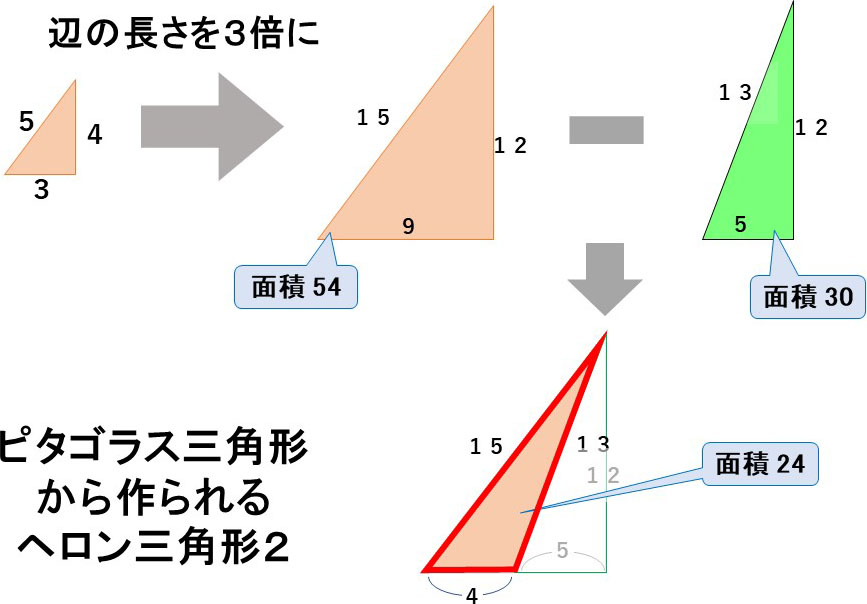
ただし、例えば「3辺が10、35、39の三角形」など、ピタゴラス三角形からは作り出せないヘロン三角形もありますから、注意が必要です。
人類にとって最も美しい「黄金比」
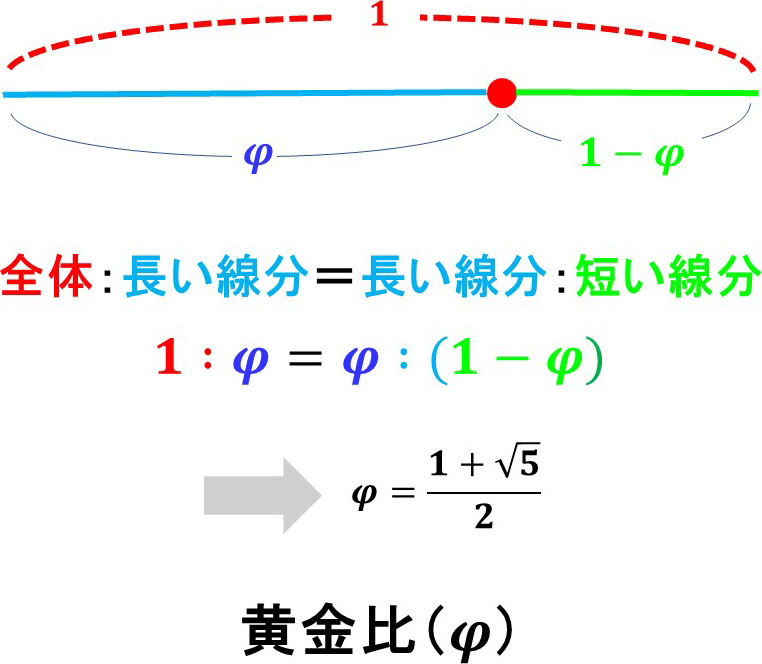
まず、黄金比について説明します。
線分を一つの点で2分することを考えます。そのとき、長い部分と短い部分との比が、全体と長い部分との比になどしいように点をとります。
このときの比が黄金比です。
古代ギリシャでの発見以来、人間にとって最も美しい比率とされています。
パルテノン神殿やピラミッド、レオナルド・ダ・ヴィンチ(1452~1519)が描いた『モナ・リザ』の顔などにその比率が見られると言われています。
黄金比は、だいたい1.618(正確には、$\frac{1+\sqrt{ 5 }}{2}$)で、よくギリシャ文字$φ$(ファイ)と表記されます。
■「黄金三角形」は最も美しい三角形?
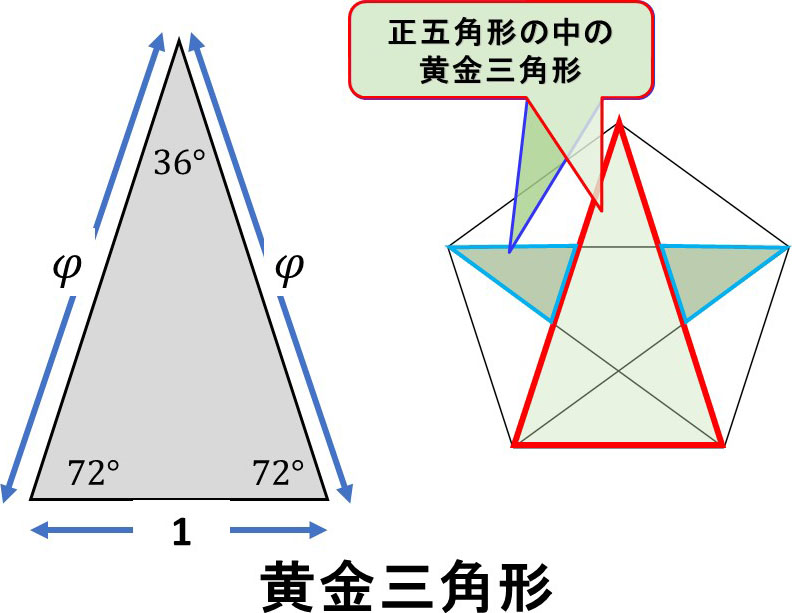
黄金三角形は、長い2辺と短い辺の長さの比が黄金比 ϕになっている二等辺三角形です。
この二等辺三角形は底角が72°、頂角が36°です。
正五角形に対角線を引くと、いろんな場所にこの黄金三角形が現れます。
皆さんも探してみてください。
ある意味では美しい?ケプラー三角形
ケプラー三角形とは、下の図に示すように三辺の長さの比が$1:\sqrt{ φ }:$φ$$になっている三角形です。
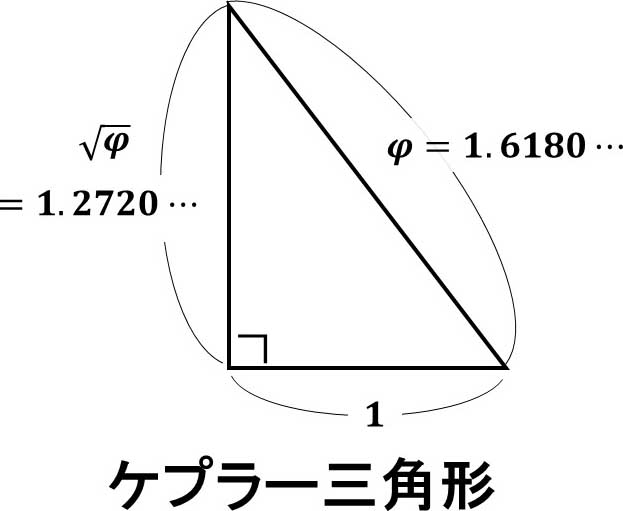
この三角形は$1:\sqrt{ φ }$の比である2辺の間の角が、なんと直角になっています。
高校生の皆さんには、3辺の長さが公比$\sqrt{ φ }$の等比数列となっている直角三角形といえばわかりやすいでしょうか。
この三角形は、ケプラーが非常に気に入っていたそうで、ケプラー三角形と呼ばれています。
実は、三辺の長さは、正数a、bに対して、その相加平均、相乗平均、調和平均になっているので、この点にケプラーは感動したとのことです。
ある意味で美しいとは思いますが、実用上の価値は?です。
曲線で囲まれた驚きの三角形「ルーローの三角形」
■ルーローの三角形
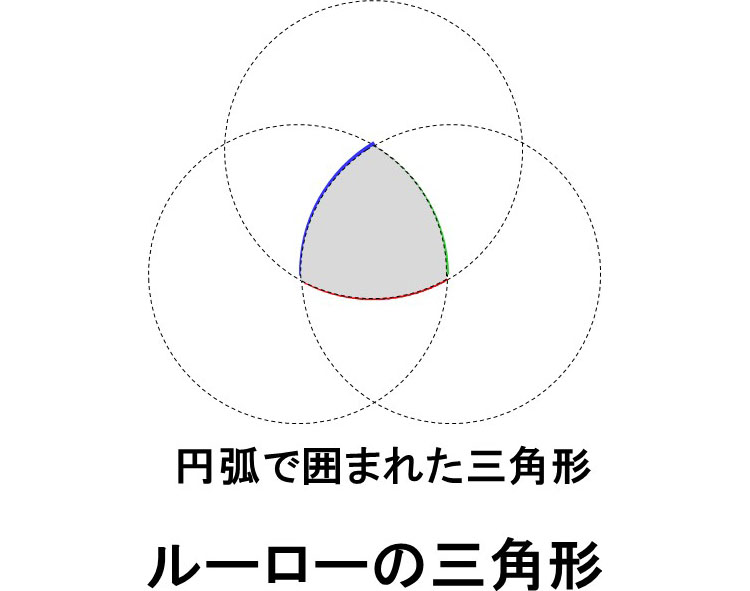
曲線で囲まれた三角形とは、奇妙ですね。これは下の図のような円の一部を辺にした三角形です。
見たことありませんか。そうです。こんな形のお掃除ロボットがありますね。
この形をルーローの三角形といいます。
ルーローとは人の名前。実はこの形、定幅図形(ていふくずけい)と呼ばれるもので、その名のとおり、どの方向から測っても幅が一定という性質があるのです。
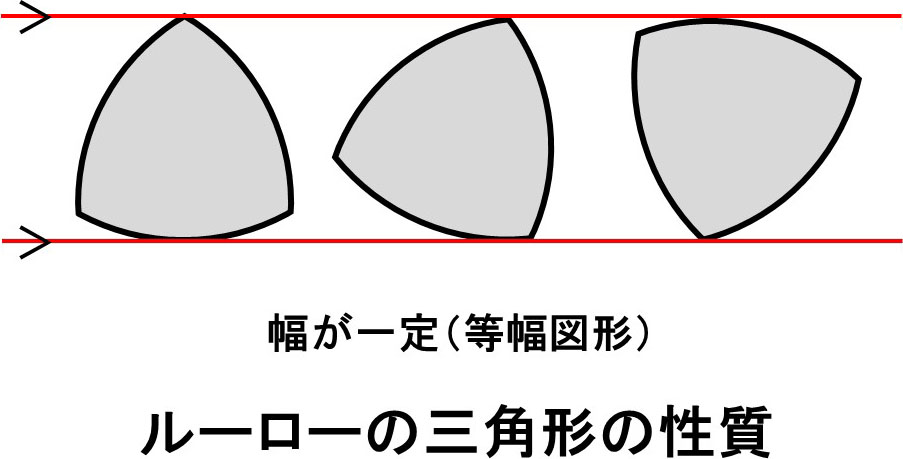
円や球は定幅図形ですが、それ以外にもあるとは、ちょっと驚きますね。この性質を利用した掘削機械もあります。
「数×三角形」三角形の形に数を並べると?
数を三角形の形に並べたものがいくつかあります。
簡単なルールの下で数を並べたものですが、いろいろと面白い関係が成り立っています。
■パスカルの三角形
これはあまりにも有名です。この記事に詳しく解説がありますので、ぜひご覧ください。
■フロイドの三角形
フロイドの三角形は整数を1から順に、次のルールで並べたものです。
- 1行目には、1個(1)を、
- 2行目には、2個(2、3)を
- 3行目には、3個(4、5、6)を
- 4行目には、4個(7、8、9、10)
なお、各行とも左端を揃えます。
実際に並べたものを見てみましょう。

この三角形には面白い性質が3つあります。気が付きますか?
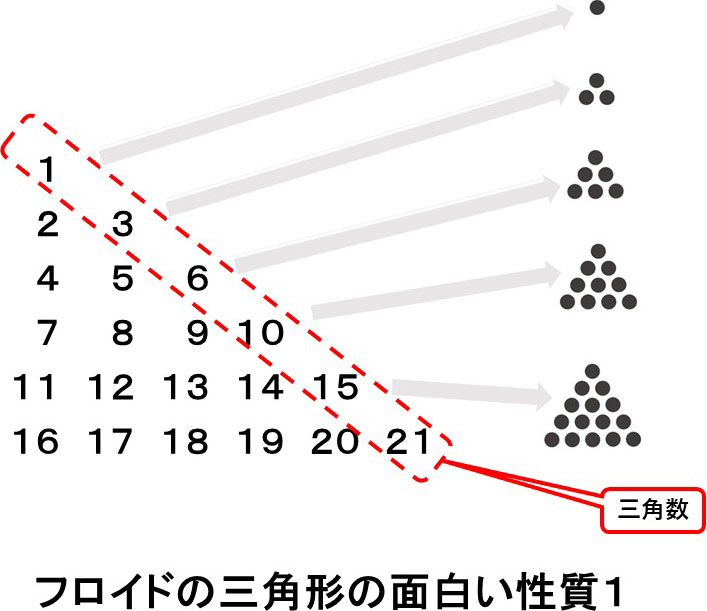
まずは、右端の斜めの数の並び。
これは三角数と呼ばれるものになっています。三角数とは、下図をご覧いただくと、どういうものか判かると思います。
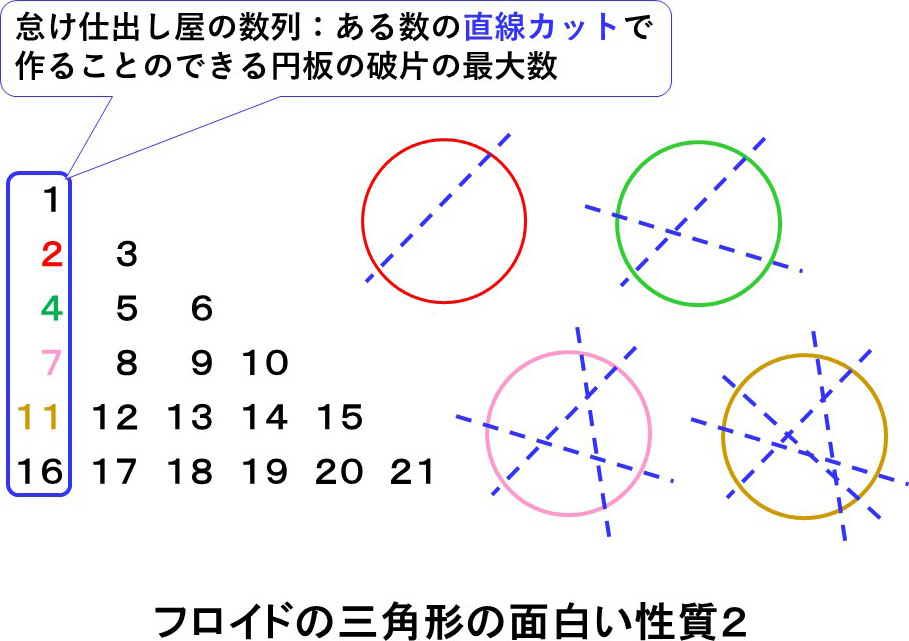
次に、左端の数の並びに注目してください。
三角数+1というだけのように見えますが、実は、『怠け仕出し屋の数列』という名前までちゃんと付いています。
ある数の直線カットで作ることのできる円板の破片の最大数となっています(難しく言うと、“最小カットによる最大領域分割数” です)。
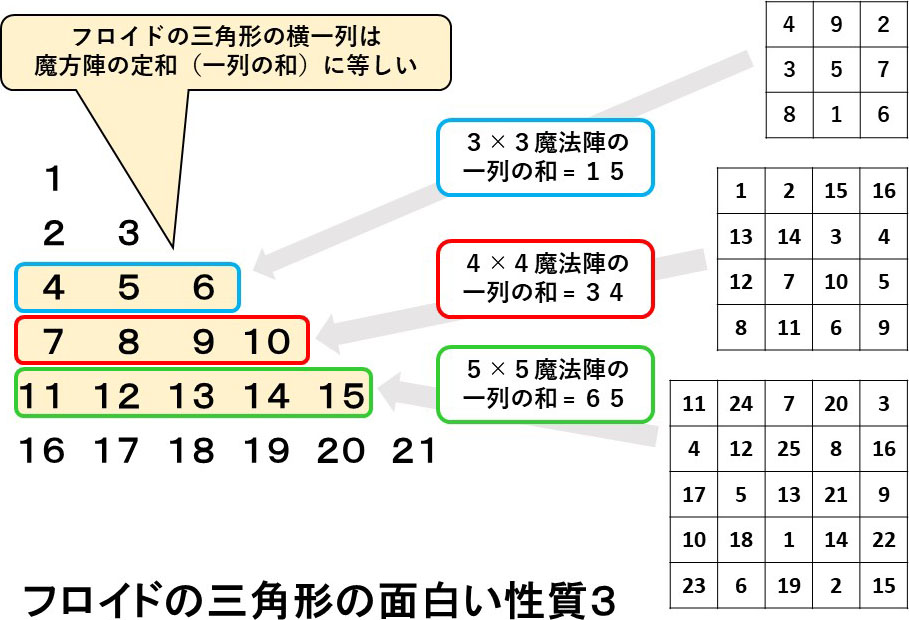
そして、各行の数の和は、魔方陣の一列(一行、対角線も含む)の和(これを定和といいます)と同じです。
例えば、3×3魔方陣の一列(一行、対角線)の和は15ですし、フロイドの三角形の3行目の和は15です。
こんな単純な並べ方の三角形なのに奥が深いですね。
このフロイドの三角形は、実はプログラミングの問題として作られたそうです。こんな問題も出来ますね。
- 問題1)直角二など辺三角形の内側に、整数を 1、2、3、…、10 と順番に並べました。整数の和はいくつでしょうか。
- 問題2)直角二など辺三角形の内側に、整数を 1、2、3、…、10 と順番に並べました。上から4行目、左から3番目の数はいくつでしょうか。
- 問題3)直角二など辺三角形の内側に、整数を 1、2、3、… と順番に並べたところ、合計が45になりました。最後の整数はいくつでしょう。またそれは、上から何行目、左から何番目にありますか。
■タルタリアの三角形
下図のような足し算の式です。

連続する整数が三角形に形にきれいに並置できることからこう呼ぶのでしょう。
見ていると規則性が何となく浮かんできますね。図形的な意味が分かるように作った(つもりの)模型をお見せします。
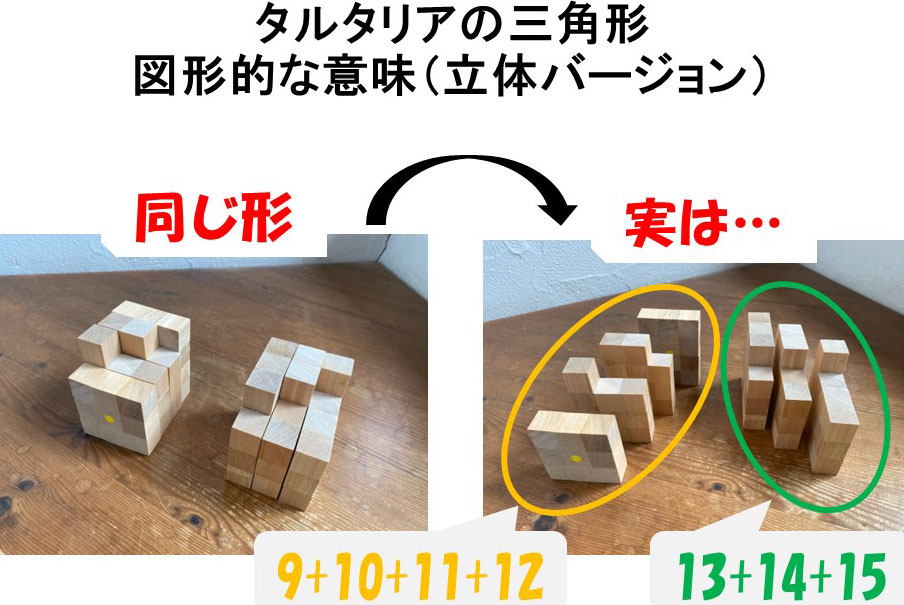
どのような整数の場合に成り立つのか考えてみるのも面白いですよ。是非チャレンジを。
終わりに
さて、紙面も尽きてきました。
このほかにも、○○三角形には、
- 数を三角形の形に並べた“ライプニッツの調和三角形”
- フラクタル図形の代表例である“シェルピンスキーの三角形”
などがあります。
これらについては、いつかの機会にご紹介することにして、今回はこれで、さようなら。
付記 【○○三角形に名を遺している数学者たち】
ピタゴラス(紀元前582~紀元前496) 古代ギリシャの数学者、哲学者。
ヘロン(10~70年頃) ギリシャの数学者。古代ローマ属州エジプトの都市アレクサンドリアで活動。
ヨハネス・ケプラー(Johannes Kepler、1571~1630) ドイツの天文学者、数学者、自然哲学者。 天体の運行法則に関する「ケプラーの法則」を唱えたことで有名。
フランツ・ルーロー(Franz Reuleaux、1829~1905) ドイツの機械工学者。
ブレーズ・パスカル(Blaise Pascal、1623~1662) フランスの哲学者、自然哲学者、物理学者、思想家、数学者。
ロバート・W・フロイド(Robert W. Floyd、1936~2001) アメリカの計算機科学者。グラフ理論で著名。
ニコロ・フォンタナ・”タルタリア”(Niccolò Fontana “Tartaglia”、1499または1500~1557) イタリアの数学者、工学者、測量士。
■三角形に関する算数クイズを解いてみよう!
■三角形を使った「感動する問題」!