ずーさん
ずーさんずーさんの『だったら算数ナゾトキ!』のページへようこそ!
この記事は、
小学生のみんなに楽しく算数にふれてほしい算数ナゾトキ★クリエイターのずーさんが、
①何かよい自学(自主学習)の算数ネタってないかな??
②もうちょっとゲームっぽく取り組める算数の問題ないの??
③ちょっとだけ、かるーく、予習できたらいいな!
の声にお応えして、
 ずーさん
ずーさんだったらコレ!算数ナゾトキ!
を、出題&解説しましょう!
そして、さらに!
今お読みいただいているパパママ、もしくは小学生のみんなとナゾトキを作成しちゃいましょう!というものです♪

体積ってなーんだ?
今回のナゾトキで扱う単元は「体積」です。
なので、体積について軽くお伝えしておこうと思うのですが……
その前に1つひっかけクイズを出します!
1㎏の鉄と1㎏の綿(わた)、重たいのはどちら?
有名なクイズなので知っていた方もいるかもしれませんが、答えは「どちらも同じ」です。
どちらも「1㎏」なんですから、同じ重さです。
 ずーさん
ずーさんでもこれ、「鉄」って言いたくなりますよね~!
どうしてひっかかってしまうかというと、「1㎏の綿」というものを想像しずらいからだと思うんです。
空気を多分に含んだふわっふわの綿を1㎏用意するとなると、かなり大きくなります。いきなり綿といわれてそんな量思い浮かべませんよね。
さて、今「大きくなる」とか「量」とか言いましたが、それが今回扱う「体積」と関係します。
ものがどれだけかさばるかが「体積」で、体積が大きいとか体積が小さいなどと表現します。
さきほどの鉄と綿で言えば、1㎏の鉄は1㎏の綿より体積が小さいと言えるわけです。
ただ……
「大きい」とか「小さい」という言葉は人によって感じ方が違って曖昧なので、
「長さ」や「重さ」、「面積」と同じようにその大きさを数値で表せると良いですよね!
そこで登場するのがこちら!
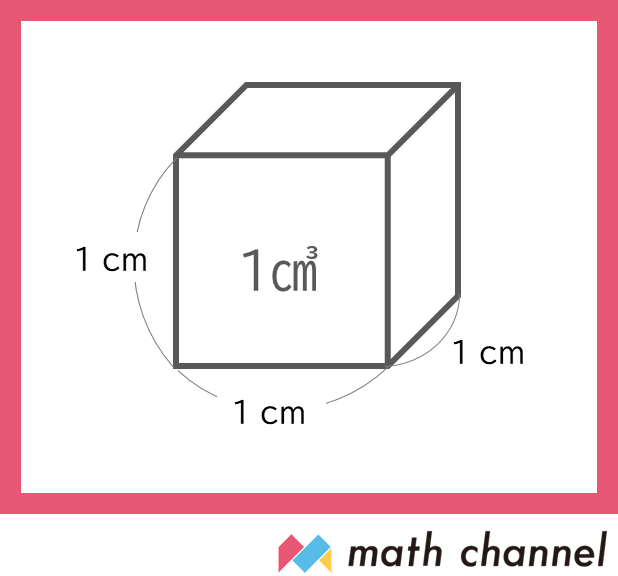
この大きさの立方体、辺の長さがどこも1㎝のサイコロのかたちの体積を1㎤と呼ぶことに決めています。
この立方体が何個分かでものの体積を表すのです。
確認してみましょう。
たとえば、この3つの形の体積、わかりますか?
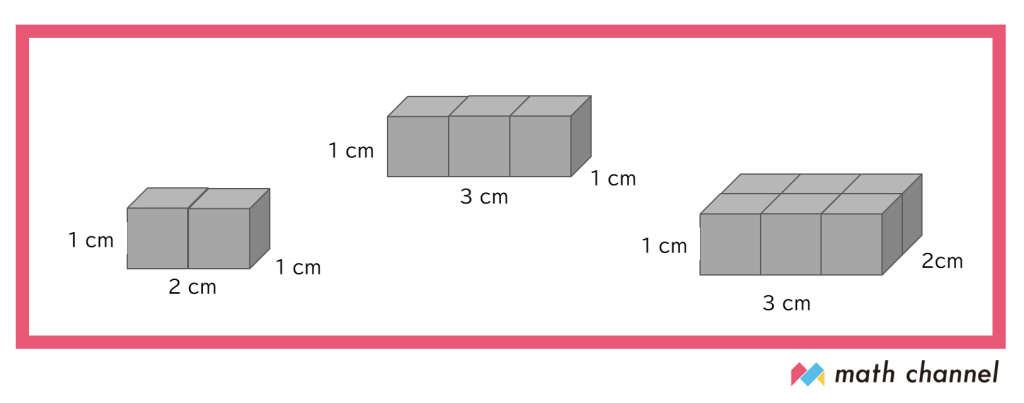
左から、2㎤、3㎤、6㎤です。
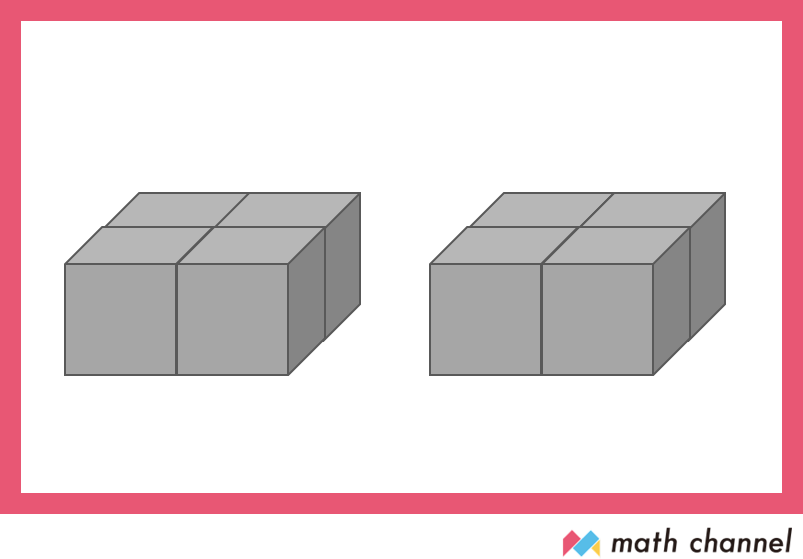
では、この立体の体積は何㎤でしょう?
基準の1㎤がいくつ分か想像してみてくださいね!
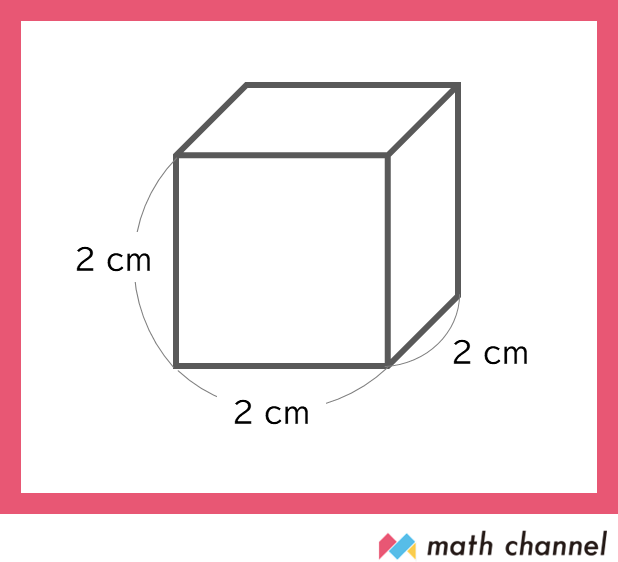
体積は8㎤です。
下の図のように段ごとにわけて数えると数えやすいかもしれません。
さあ、体積のことがわかってきましたか?
それでは、今回の謎を出題しましょう!!
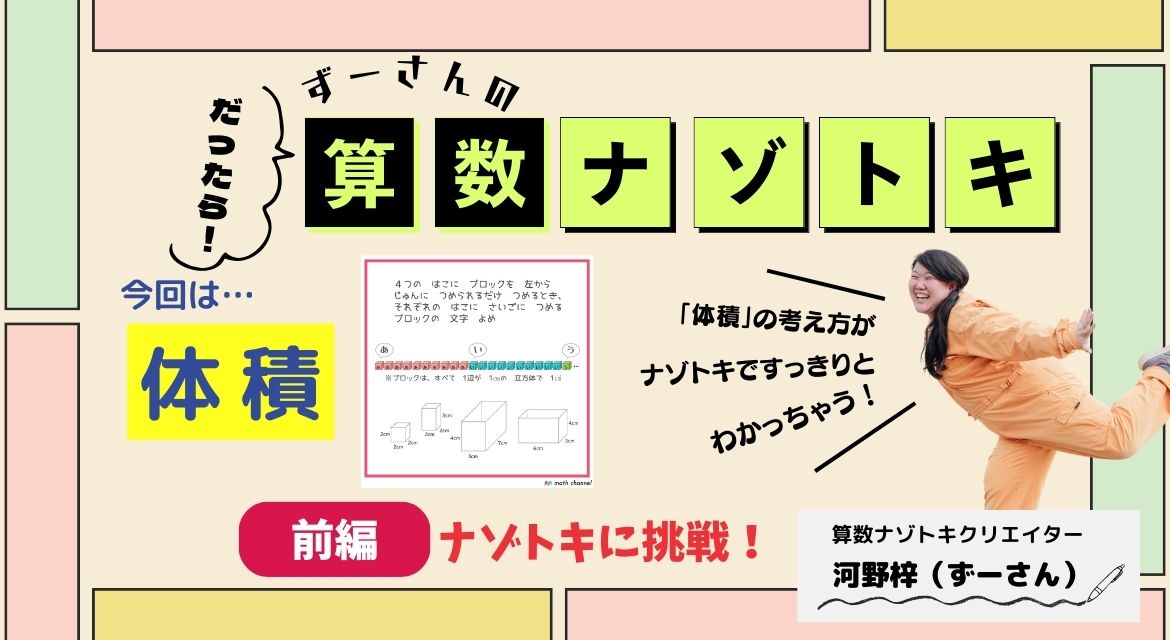
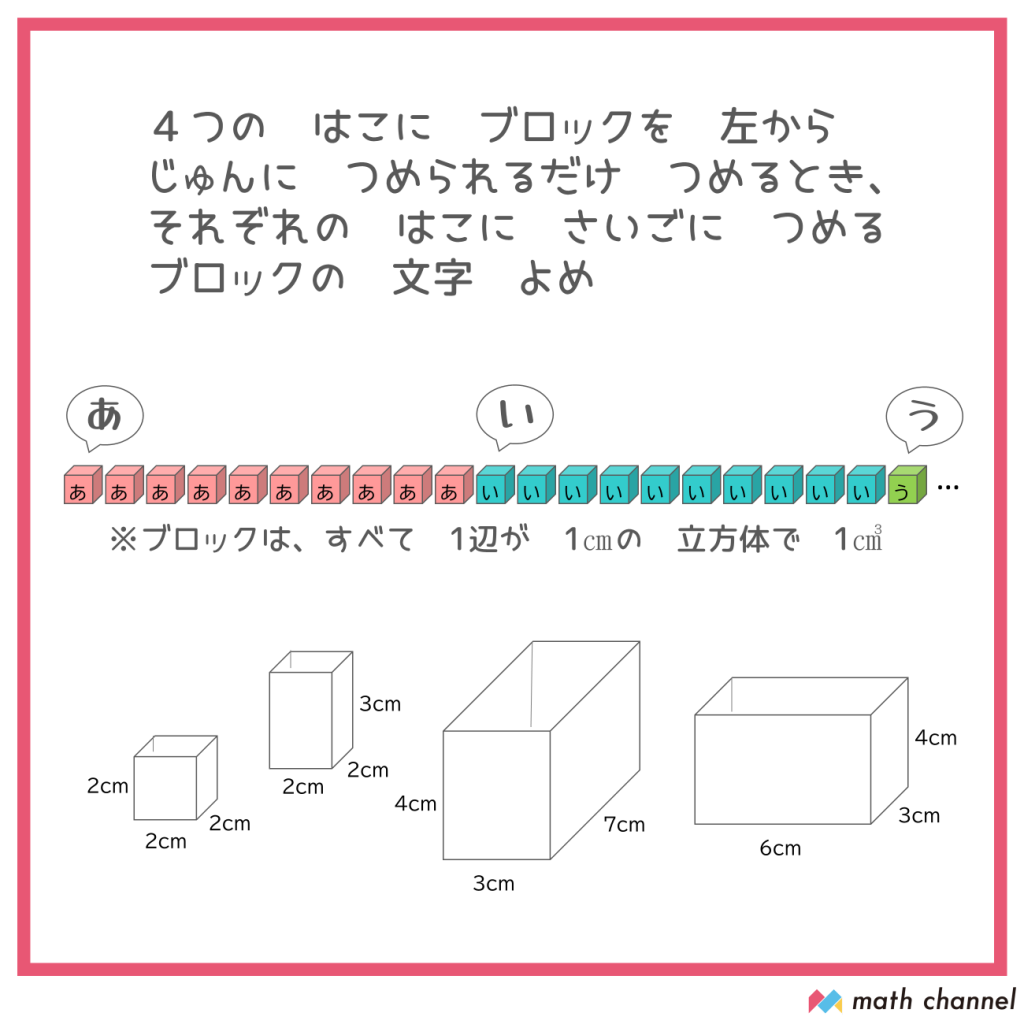
今回の問題は、こちら!
↓注意(ちゅうい)!この下にヒントがあります↓
ヒント1
ひらがなが書かれた小さいブロックがたくさんならんでいます。
これらのブロックの体積はわかりますね?そう、1つ1㎤です。
さて、これらのブロックは同じ文字が書かれているものが何個ずつならんでいるのでしょう?
↓次のヒント↓
ヒント2
10個ずつであることを確認できましたか?
それらを左からつめていくようです。いちばん左の箱にはいくつのブロックが入るのか想像してみましょう。
↓次のヒント↓
ヒント3
8個ですよね。ということは、左の箱に最後につめるブロックは左から8ばんめの「あ」のブロックです。
残りも同じように考えると……?
(この先に解答があります)
…
…
…
解答
答えは「あいさつ」でした!
どうでしょう、できましたか?
解説
この問題は、まず、それぞれの箱にいくつブロックを詰めることになるのか考えるといいです。
ここがまさに今回の「体積」に関係する算数部分ですよ!
ヒントでもお伝えした通り、
いちばん左の箱の体積は8㎤、
左から2番目の箱の体積は12㎤、
左から3番目の箱の体積は84㎤、
いちばん右の箱の体積は72㎤、
です。
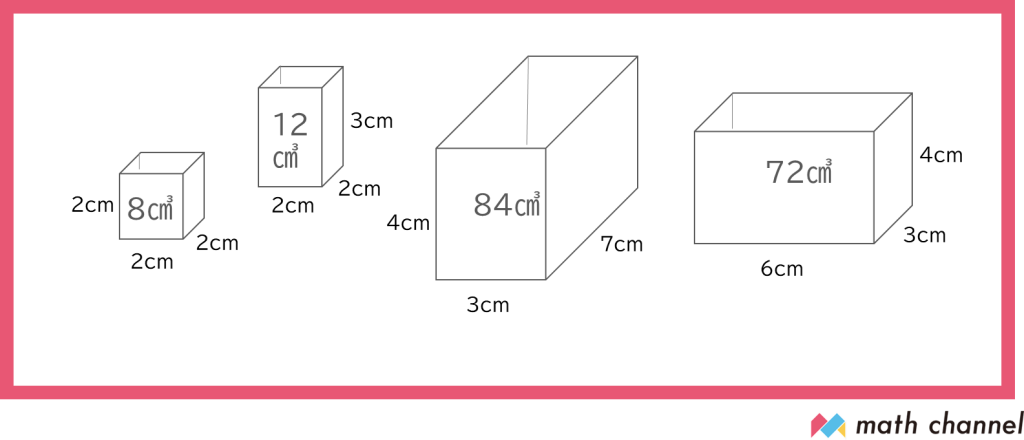
これで、それぞれの箱に入るブロックの数がわかります。
左から、8個、12個、84個、72個ですね。
ならんだブロックの左からつめていくと、
左から8ばんめが左の箱の最後に入るブロック、
左から8+12=20(ばんめ)が2つめの箱の最後に入るブロック、
左から8+12+84=104(ばんめ)が3つめの箱の最後に入るブロック、
左から8+12+84+72=176(ばんめ)が右の箱の最後に入るブロックになるはずです。
さて、左から8ばんめ、20ばんめ、104ばんめ、176ばんめのブロックには何の文字が書かれているでしょうか?
今回はここも算数部分ですよ!
文字は「あ」から順番に同じ文字が10個ずつ並んでいますから、
8ばんめ→1~10の「あ」
20ばんめ→11~20の「い」
104ばんめ→101~110の「さ」
176ばんめ→171~180の「つ」
と、なるはずです。
したがって答えは「あいさつ」となります。
いかがでしたでしょうか。
今回は「体積」に関する算数ナゾトキを出題しました。
まずは、
ものの大きさ、どれだけかさばるかを「体積」という言葉で表すこと、
どの辺も1㎝のサイコロの形(立方体)の大きさが1㎤という体積であること、
それがいくつ分であるかを考えれば体積を数字で表せることを
体感してくれたら嬉しいです。
ちなみに、体積を求める公式を知っている人は、なんでその式で体積を求められるのか今回のナゾを通してもう一度考えてみましょう!
後編では、いよいよこれと似た謎解きを作っていきますよ!
それでは、また後編の記事でお会いしましょう!
お読みいただき、

(文責:河野梓)
毎週出題しています!
こちらの公式LINEアカウントに登録いただくと、毎週算数ナゾトキが届きます!
友だち登録してスキマ時間にぜひ挑戦してみてください!
『算数ナゾトキ20』発売中☆
また、math channelではいろんな算数ナゾトキを20問集めた問題集や九九に関するナゾトキがつまった九九ナゾも販売しています。