「中点三角形」と「中線三角形」って知っていますか？～三角形ひとつをじっと眺めていると……～

こんにちは、みうらです。

三角形に関して、これまで何回かお話してきました。

今回は三角形ひとつをじっと眺めていると、その内部から生まれてくる新しい三角形を考えてみましょう。
そこからは思いがけない数学の美しさが見えてきますよ。

この記事では、三角形の中に、もうひとつ三角形をつくる——そんな不思議で、少しワクワクする話をします。

「中点三角形」と「中線三角形」とは

「三角形の中に三角形」と聞いて、どんなものを思い浮かべますか。
すぐに連想できるのは、3辺の中点を結んでできる三角形でしょうか。これには、よく知られた名前があり、「中点三角形」と呼ばれます。

さて、中点三角形の面積は、元の三角形のどれくらいでしょうか。
これは比較的簡単です。中点同士を結ぶと、三角形は4つの合同な小さな三角形に分かれます（証明には中点連結定理を用います）。したがって、中点三角形の面積は元の三角形の 4分の1 になります。

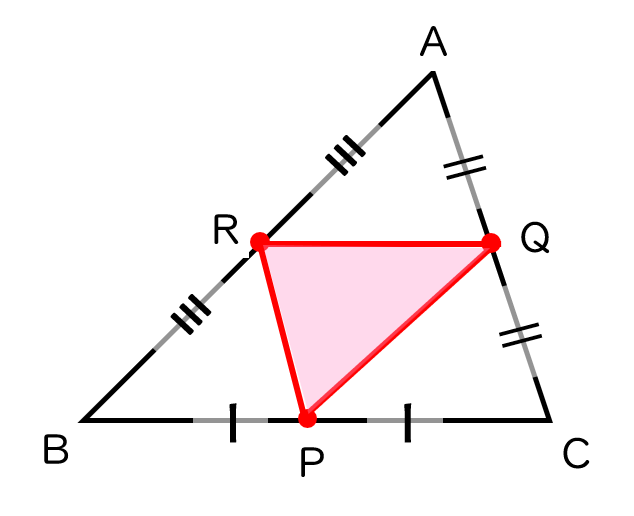
では、次の三角形はどうでしょう。
三角形の3本の中線（頂点と向かい合う辺（対辺）の中点を結ぶ線分）の長さを3辺とする三角形です。これを指す一般的な名称はあまり定着していません。ここでは、中線三角形と呼ぶことにします。

ここで疑問が湧きます。「三角形が作れるための3辺の長さの条件」を思い出すと、2本が極端に長ければ三角形を作れない可能性があります。

そもそも、このような中線三角形は本当に存在するのでしょうか。

中線三角形の作図

そこで、実際に作図して確かめてみましょう。描き方はとても簡単です。

三角形ABCを用意し、BCの中点をP、CAの中点をQ、ABの中点をR とします。

1. 線分 RQ を CA の外側に向かって延長する
2. RQ と同じ長さだけ延長した先の点を S とする
3. すると、三角形 APS が、中線3本の長さを持つ三角形（＝中線三角形）になる

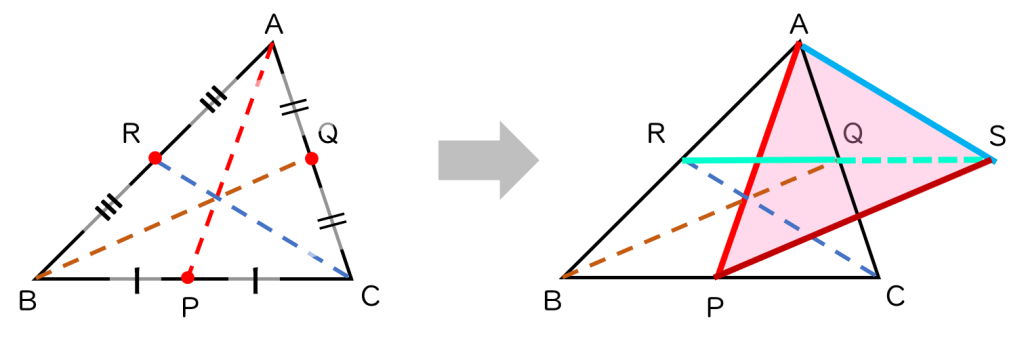
証明のポイントは、平行四辺形の性質です。

PS = BQ
→ QS ∥ BP かつ QS = BP より、四角形QSPBは平行四辺形
→ PS = BQ

SA = CR
→ AQ = QC、RQ = QS より、四角形ARCSは平行四辺形
→ SA = CR

したがって、三角形ABCの3本の中線AP、BQ、CRの長さを3辺に持つ中線三角形は確かに存在することが分かります。

中線三角形の面積は？

いよいよ気になる面積の話です。
中線三角形の面積は、なんと—

元の三角形の 4分の3

になります。

この証明には、三角形の面積が、「底辺の長さ × 高さ ÷ 2」　で求められることだけしか使いません。

では、実際に導いてみましょう。
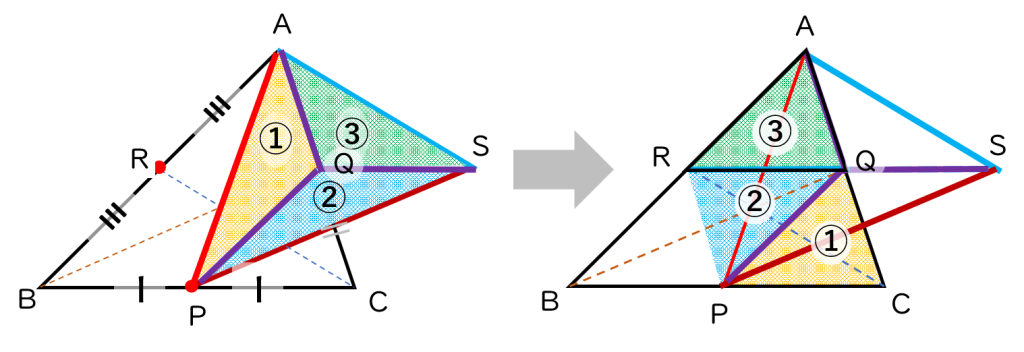
先ほど作図した中線三角形を３つの小さな三角形（三角形APQ、三角形AQS、三角形QPS）に分割します。（下図の左側）

高さと底辺を丁寧に確認すると、

・三角形APQの面積 ＝ 三角形PQCの面積
・三角形AQSの面積 ＝ 三角形ARQの面積
・三角形QPSの面積 ＝ 三角形RPQの面積

であることが分かります。（下図の右側）

【参考】
高校生レベルの数学に挑戦したい方は、
・中線定理で中線三角形の3辺の長さを求める
・さらにヘロンの公式で面積を計算する
というアプローチも可能です。
ただし、計算（因数分解や式の展開）はかなり煩雑なので、手計算には根気が必要です。数式処理用AI（例：Wolfram Alpha など）を使えば、計算の確認が楽になります。

おわりに

三角形の中に現れる三角形には、今回紹介した2種類のほかにも、内接円から生まれる接触三角形、垂線で作られる垂足三角形など、さまざまな三角形が考えられます。

そこからさらに多くの興味深い図形へと話題が広がっていきます。

これからも、“三角形の中の三角形”の魅力を、少しずつ掘り下げていく予定です。ぜひ楽しみにしていてください。

（文責：みうら）

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

文系オトナですが、今から数学を楽しめますか？ [ math channel ] 価格：1,760円（税込、送料無料) (2025/7/3時点) 楽天で購入

数学博識王みうらの人気記事　こちらもどうぞ！