こんにちは、うっつんです。
今日はアルキメデスの立体というものを紹介したいと思います。
アルキメデスの立体は、別名半正多面体とも呼ばれていて名前の通り正多面体に深く関係しています。
この2つの関係を知ることで立体図形を捉えやすくなります。
実際に問題も1問入れていますので、ぜひ考えてみてください!
正多面体について
まずは、正多面体について紹介します。
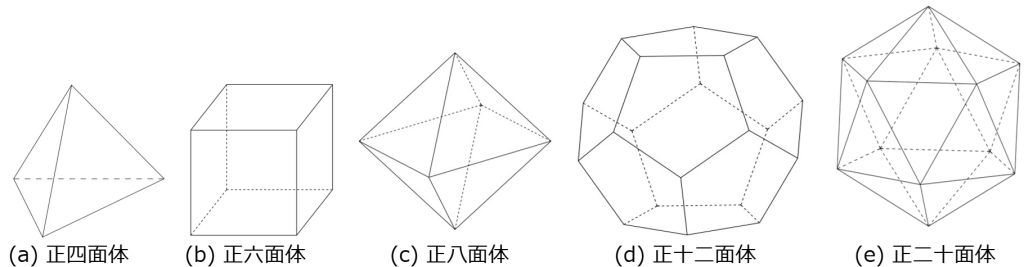
正多面体には、正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体の5つがあります。
これらの立体の特徴は全ての面が合同な正多角形で構成されていて、全ての頂点に同じ数の面が集まっていることです。
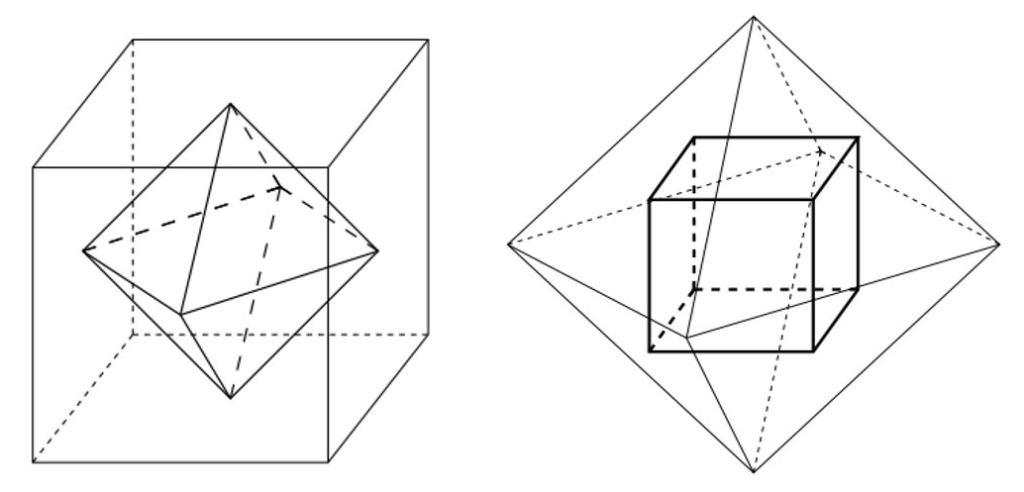
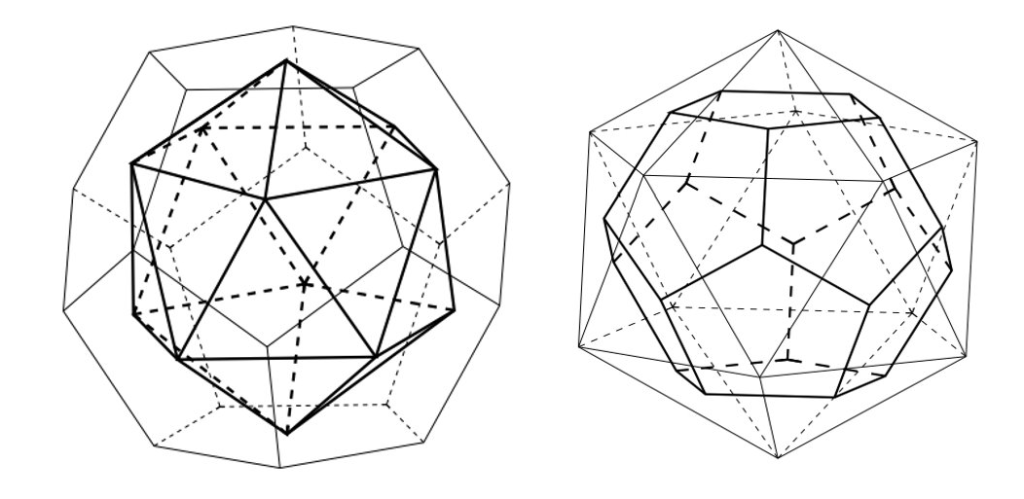
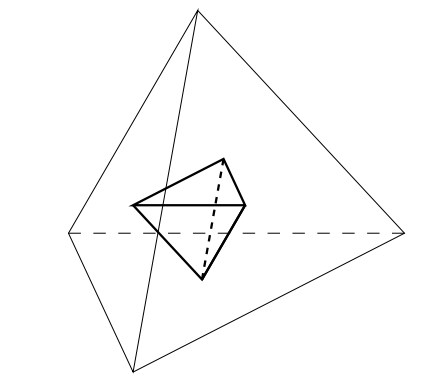
また、正多面体には、双対の関係というのがあります。
例えば、正六面体と正八面体は双対の関係で、それぞれの面の中心を結ぶともう片方の立体が出てきます。
正十二面体と正二十面体も双対の関係、さらに正四面体は自身と双対の関係にあります。
双対の関係にある立体の特徴としては、辺の数が同じで、面と頂点の数が反対になっているという特徴もあります。
アルキメデスの立体(半正多面体)
次に、今回のメインテーマ「アルキメデスの立体」の紹介をします。
アルキメデスの立体は、2種類以上の正多角形で構成されていて、全ての頂点に集まる面の形状と数が同じ立体です。
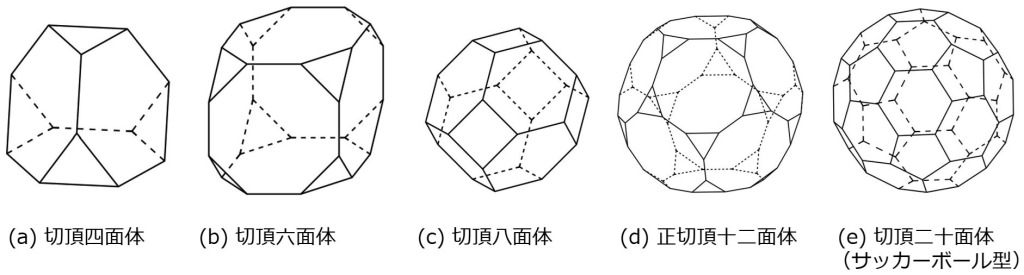
例えば、切頂四面体は正三角形と正六角形の2種類で構成されていて、全ての頂点に正六角形が2枚、正三角形が1枚集まっています。
一部この特徴を満たしていますが対称性が低いものを除いて13種類がアルキメデスの立体と呼ばれています。
下にそのうちの切頂多面体と呼ばれる5つを紹介します。
欠けている部分を想像しよう (問題にチャレンジ!)
それでは、正多面体とアルキメデスの立体の関係を考えていきましょう。
まず、 下の展開図を見て元の立体を想像してみてください。
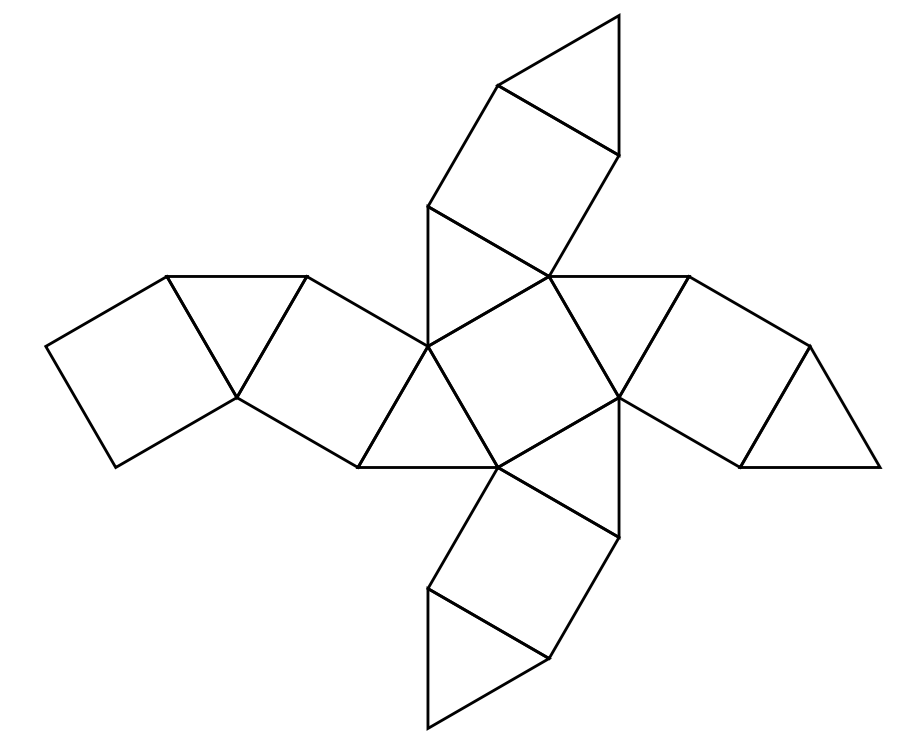
これは最初はとても難しいと思われます。
そこで面の構成を見てみます。正三角形が8枚、正方形が6枚あります。
この数に少し注目してみます。
例えば、正六面体には頂点が8個、面が6枚あります。
これと関連付けてみましょう。
正六面体の頂点を適当に切り落とすと正三角形が出てくるので、さらに上手く全ての辺の中点を通るように切断すると頂点だった場所に正三角形の面が、元々正方形の面だったものが半分の大きさの正方形になります。
この操作により展開図と面の構成が同じになります。
実はこの立体は立方八面体と呼ばれるアルキメデスの立体の一つです。
また、この立体は同様に正八面体の頂点を各辺の中点で切り落としてもできます。
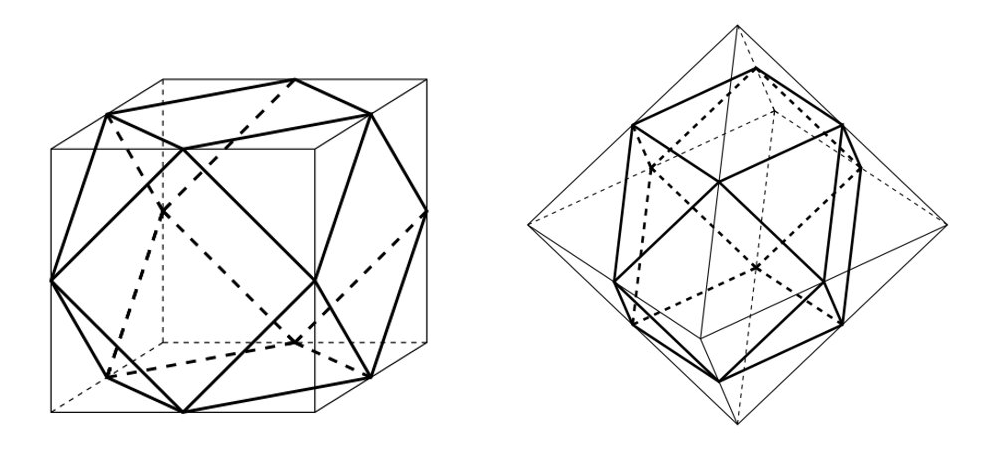
このように、アルキメデスの立体は正多面体を切り落としてできる立体が多いです。
切頂多面体と呼ばれるものは、切り落とした時にできる正多角形の辺の長さと元の面に残る正多角形の辺の長さが同じになるように切ります。
例えば、切頂四面体は三等分に、切頂六面体は$1:\sqrt{2}:1$に辺を分割します。
アルキメデスの立体は一見複雑に見えるのですが正多面体との関係を考えることで特徴を捉えやすくなります。
下に立方八面体以外で正多面体の頂点を切断することで出てくるアルキメデスの立体を紹介します。
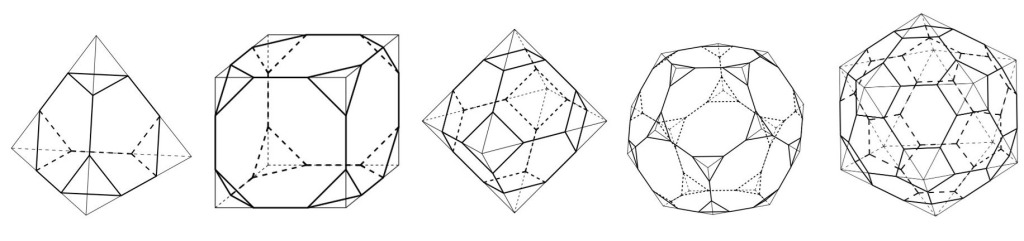
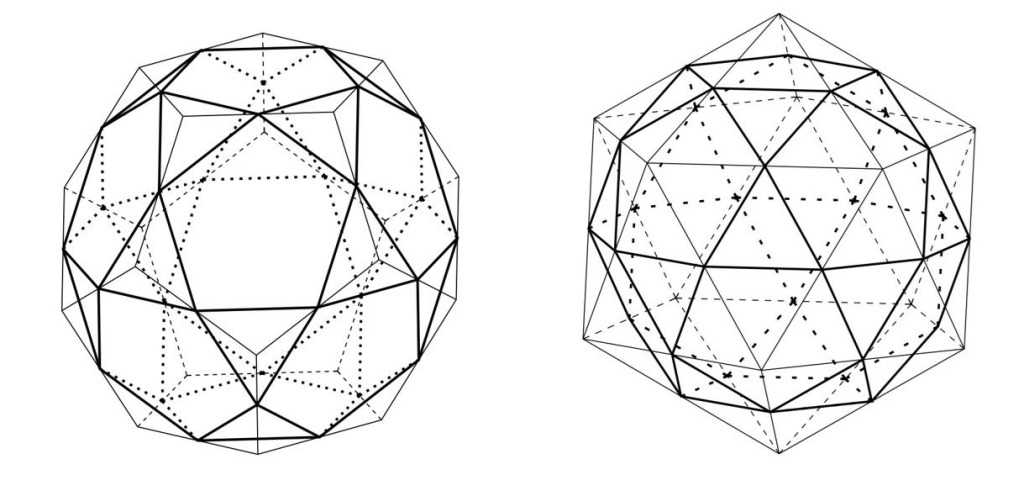
様々な視点を持って立体の特徴を捉えよう
今回のアルキメデスの立体のように立体図形の特徴を捉えるためには一つの視点だけでは難しいです。
正多面体との関係や他の視点をもっておくことで、新たな特徴が見えてくることがあります。
中学、高校受験で出てくる立体の問題では投影図や断面図などの平面に情報を整理することが多いですが、それも視点の一つになります。
また、アルキメデスの立体は最難関高校受験でたまに出題されますが、一つの視点では考え方や計算が大変でも見方を変えると易しくなることがあります。
ぜひ様々な立体の面白い特徴を調べて視点をたくさん手に入れてみてください。
(文責:宇都木一輝)