こんにちは、算数ナビゲーターの滝澤です。
今回は、平面図形についてお話をしたいと思います。
平面図形と言えば、中学受験の算数の中でも多くの学校で出題される最重要単元の1つです。
私は2大重要単元は平面図形と速さだと言っています。この2つの単元は多くの中学で頻繁に出題されますし、また差がつきやすい単元なのです。
もし、今平面図形が苦手だなと思っている方がいらっしゃったら早めに対策をうつことをおすすめします。
なぜ平面図形は出題されやすいのか
平面図形がよく出題される理由、それは、中学数学でも扱う内容だからです。特に相似や面積比などの問題は中学でも習います。
ただし、解き方は小学生とは少し違いますね。数学では未知数をxやyとおいて等式を作って答えを求めるのが一般的な解法です。
しかし、等式をつくるための図形の描き方や見方、さらには解法・知識は中学受験算数のときと変わらないものがたくさんあります。
また、平面図形の解法知識は、立体図形(空間図形)でも応用されます。さらに高校数学で学習するベクトルにもつながっていきます。
このようにも中学・高校を通じて学習する内容の礎ともいうべき単元ですから、今のうちに平面図形の問題の解き方は身に着けておいたほうがよいでしょう。
平面図形の問題を解くためにセンスは必要?
平面図形というとよく「図形センス」ということを言われますよね。
なんだかセンスと言われると、平面図形の問題を解くには持って生まれた才能のようなものが必要だと誤解している方も多いように思います。
私は平面図形の問題が得意になるために必要なことは、解法知識の習得、つまり努力と正しい暗記だと思っています。公式などの丸暗記ではありません。
なぜその解き方で解けるのかということもしっかり暗記することが大切なのです。
面積比の解法知識
今回は中学受験算数の中でも大変よく出題される面積比の解法知識についてお伝えできればと思います。
まずはこちらの問題をごらんください。
【問題】
下の図のような三角形ABCと三角形FDCがあり、点Dを辺BCのちょうど真ん中にとります。
辺ABと辺DFの交点をEとすると、DE:EF=3:1です。
CA:AFを最も簡単な整数の比で表しなさい。
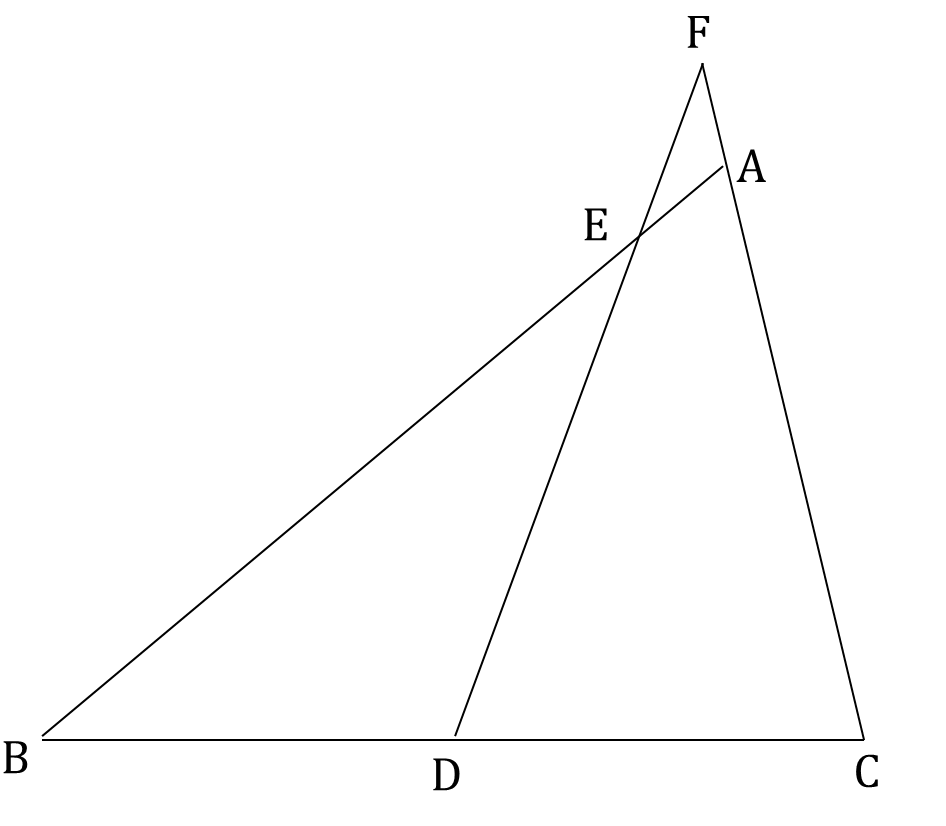
メネラウスの定理で解ける。
この問題は実は中学数学で扱う、「メネラウスの定理」を使うと簡単に解くことができます。
メネラウスの定理とは、この問題の図でいうと、
が成り立つという定理です。これを使うと
$$\frac{FA}{AC}×\frac{2}{1}×\frac{3}{1}=1$$ ですから、$\frac{FA}{AC}=\frac{1}{6}$となり、CA:AF=6:1になります。メネラウスの定理の丸暗記
メネラウスの定理の覚え方の一つをお教えします。
まずこの図全体をキツネの顔だと思います。
そして、FとBが両耳の先端、AとDは耳の付け根、Eが頭の上で、Cがあごの先だと思います。
このように、各頂点の位置関係を顔の部分として認識してしまうのです。
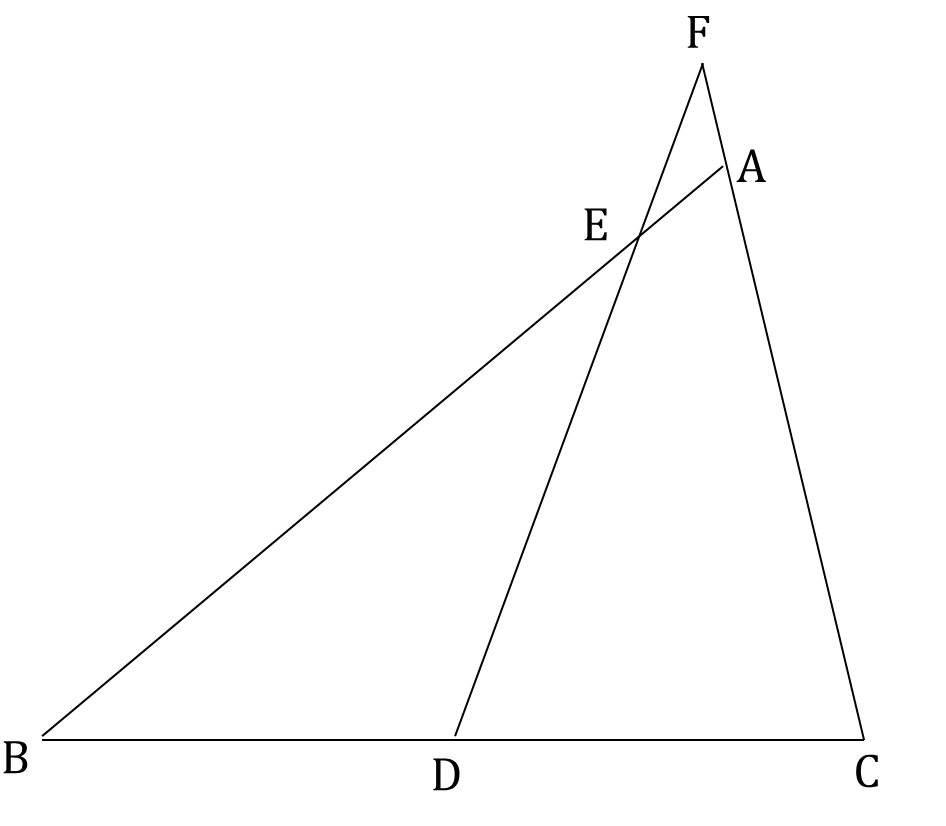
そして、次にそれぞれの顔の部分の順番を覚えます。
左耳の先端→耳の付け根→あご→右耳の先端→耳の付け根→頭の上→左耳の先端 の順だと覚えると
F→A→C→B→D→E→Fとなり、この順に分数の上→下→上→下→上→下と配置して
$$\frac{FA}{AC}×\frac{CB}{BD}×\frac{DE}{EF}=1$$と覚えるのです。これを覚えてしまえば、あとは数字をあてはめれば正解が出ます。
でもこれはただの丸暗記です。
これではなぜそうなるのかわかりませんよね。
中学生でこの問題を解ける生徒でも、メネラウスの定理をただ丸暗記して、問題によってこの公式をあてはめているだけの生徒も多いと思います。
もちろんそれで正解できる問題も多いので、一概に悪いことだけではありませんが、できればなぜそうなるのかもわかってほしいものです。
公式はその形だけでなく、どのように導出できるかをしっかり覚えておきたいものです。これが正しい暗記です。では、どのように何を覚えるべきなのかをお話しましょう。
なぜメネラウスの定理が成り立つのか
中学受験算数では面積比の基本図形としてこのような形を学習します。
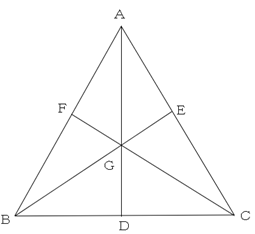
これは「ベンツ切り」と呼ばれたりします。自動車のベンツのエンブレムのような形に三角形を切り分けている図ということですね。
この図では三角形の面積比と線分の比が等しい組合せがいくつか見られます。
例えば、BD:CDと面積比が等しいのは三角形ABD:三角形ACDですね。ほかにも三角形GBD:三角形GCDや、三角形ABG:三角形ACGはBD:CDと等しくなります。
理由はわかりますか?
高さが等しいので、面積比と底辺の長さの比が等しくなるからですね。
この中でも特に重要なのは、三角形ABG:三角形ACG=BD:CDという関係です。
さらに、AG:GDと面積比が等しくなる図形は三角形ABG:三角形GBDがありますね。
ほかにも三角形ACG:三角形GCDや四角形ABGC:三角形GBCがあります。
この中でも特に重要なのは、四角形ABGC:三角形GBC=AG:GDという関係です。
さて、メネラウスの定理の式をこの図で考えると、
$$\frac{AE}{EC}×\frac{CB}{BD}×\frac{DG}{GA}=1$$となります。
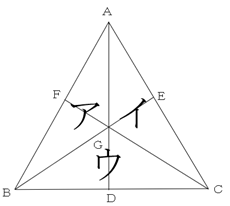
図のように三角形ABGをア、三角形ACGをイ、三角形BCGをウとすると、
AE:EC=ア:ウ、CB:BD=イ+ア:ア、DG:GA=ウ:ア+イ
ですから、
$\frac{ア}{ウ}×\frac{(イ+ア)}{ア}×\frac{ウ}{(ア+イ)}$となり、約分すると確かに積が1になることがわかりますね。なぜ成り立つのかを考え、理解し、覚えよう!
今回はメネラウスの定理を例に出しましたが、今まで習ったことの中でも、
「なぜ三角形の内角の和は180°なのか」
「なぜ円の面積は半径×半径×円周率なのか」
など、公式を丸暗記するのではなく、厳密ではなくともなぜその公式が成り立つのかという知識もしっかり頭において学習していくと平面図形の問題はとても楽しく解くことができると思います。
「こうやって解くんだよ、覚えなさい。」ではなく
「こうやって解くんだよ。なぜこうなるかの理由はこうだからだよ。
理由がわかったら手順を覚えるようにしなさい。」
というように私たちも子供たちに教えるようにしています。平面図形の問題が好きになるためには、どうやって解くのかだけでなく、なぜその方法で解けるのか?という疑問に徹底的に向き合うことが必要なのだと思います。
平面図形の問題を動画配信しています。
実は私はYouTubeのショート動画で「スキマで算数 平面図形編」というタイトルで平面図形の問題解説をしています。そろそろ100本になりますので、なにかしらの形でまとめたいなとも考えています。今回の問題のようなベンツ切りの問題はこちらです。
もしよろしければご覧ください。
『線と四角と表でわかる つるかめ算』(日東書院本社)発売中!

「つるかめ算」「和差算」「濃度算」「旅人算」などの特殊算を図解で解説している本『線と四角と表でわかる つるかめ算』(日東書院本社)が発売中です!
文責:滝澤幹
著者プロフィール

タッキー先生(滝澤 幹 たきざわ かん)
中学受験算数ナビゲーター
御三家筑駒中学受験専門塾にて指導歴30年。「算数の楽しさは正解だけではない」「すべての小学生に算数の難問を解く楽しさを知ってほしい」と思い、math channnelに参加。算数表現力ゼミを主催。共著書に『親子で楽しむ!中学受験算数』(平凡社刊)がある。









