大きな数といえば、無量大数。非常に大きな数を表す言葉で、小学校の教科書でも「大きな数についている名前」として紹介されていて、記憶に残っている人も多いはずです。
1のあとに0が68個並べると「1無量大数」となりますが、あまりにも大きくて身近に感じることはできません。1兆は1のあとに0が12個続きますので、1兆の1兆倍の1兆倍の1兆倍の1兆倍の1億倍が「1無量大数」ということになります…という説明をしてもいまいちピンとこないのが正直なところ。
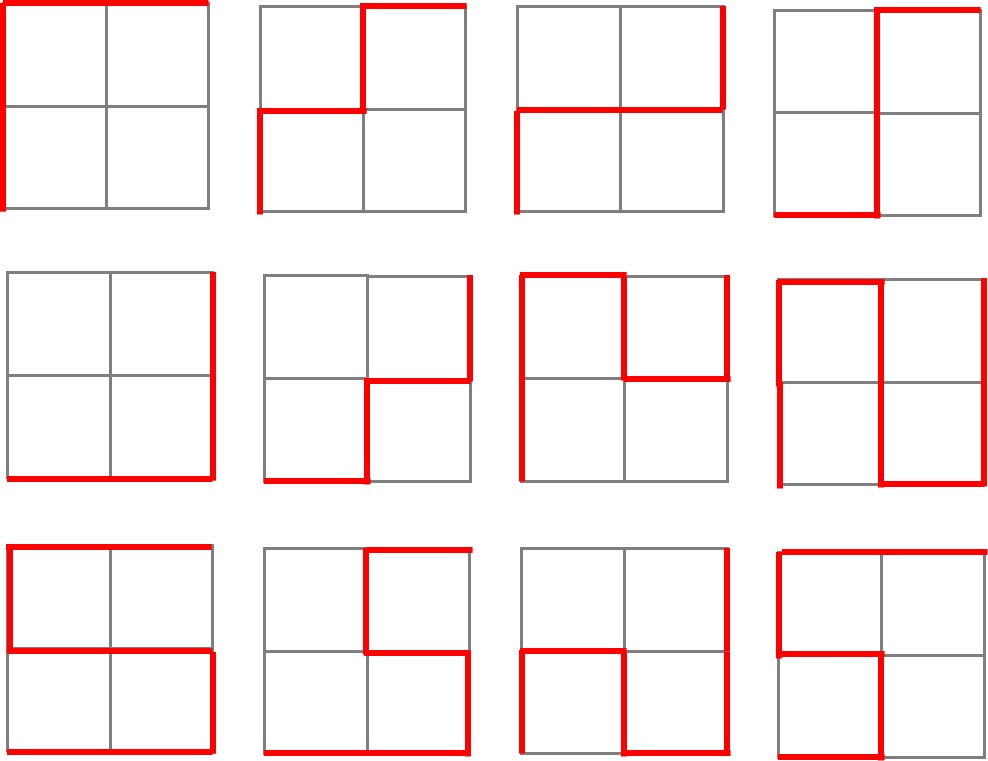
ですが、そんな「無量大数」が意外なところに潜んでいるのです。「ある地点からある地点まで行くための行き方」に、無量大数が潜んでいます。たとえば以下のようスタートからゴールまで進むとしたとき、何通りの行き方があるでしょうか。遠回りしてもいいですが、1回通った道は、交差点も含めてもう一度通ることはできないとします。

上の図のような道のことを道によって描かれている正方形の数に注目し「 2×2マスの道」と呼ぶことにします。この「2×2マス」の場合は、実際に数えていくと答えは12通りになります。
これは実際に描いて調べることもできますので、出題してみても面白い問題かもしれません。ですが、さらにマスの数を増やしていくと、とても大変なことが起きます。3×3マスの場合、何通りとなるでしょうか。
マスの数がちょっと増えるだけで、一気に行き方が増えていく?
なんと、3×3マスの場合、答えは184通りの行き方があります!
描いて調べるにはちょっと難しいかもしれません。2×2マスが12通りなので、それと比べると1マスずつタテと横に増えるだけで、一気に行き方が増えます。
さらに4×4マス、5×5マスと考えていくと、その増え方はとてつもないものとなります。下に10×10マスまでの行き方の場合をまとめてみました。
1×1マス…2通り
2×2マス…12通り
3×3マス…184通り
4×4マス…8512通り
5×5マス…126万2816通り
6×6マス …5億7578万564通り
7×7マス…7893億6005万3252通り
8×8マス …3266兆5984億8698万1642通り
9×9マス…4104京4208兆7026億3249万6804通り
10×10マス…1秭(ジョ)5687垓5803京464兆7500億1321万4100通り
2×2マスと3×3マスの場合を比べると184÷12=15.333……と、行き方が15倍くらいに増えていますが、3×3マスから4×4マスまでには50倍近く増えており、5×5マスではさらに100倍以上増えているのがこの問題の特徴です。
このように、問題の大きさに対して、答えが非常に大きくなって答えを出すのが難しくなることを「組合せ爆発」といいます。問題はあくまでも「n×nマスの格子状の道があり、同じ道を通らずにスタートからゴールまでいく行き方は何通りか」という単純な状況にも関わらず、nが1つ増えるだけで答えが爆発的に増えていくのです。

ちょっとした余談ですが、「1秒に1通り見つけたとして、すべての場合を数えるのにどれくらいの時間が必要か」を考えてみましょう。
先ほどあげたように、4×4マスのときを数えた場合は8512通りなので8512秒かかります。およそ2時間22分の時間を必要とします。
この時点で自分で探すことが不可能に近いことがお分かりいただけるかと思います。
さらに5×5マスとなると631408秒です。つまり、7日と7時間23分28秒。たった5×5マスの格子状のマスに寝ずに本気で集中して向き合えたとしても、1週間以上向き合ってようやく数え終わる、というわけです。
(ちなみに6×6マスだと3332日、つまり9年以上かかります。笑)
そしてついに現れた、無量大数!
10×10マスまでは紹介しましたが、これよりもう少しだけ増やした、17×17マスの場合を考えると、ついに無量大数を超えます。その数は、
6344814611 2379639713 1029754079 5524400449 4439868664 8069364636 9387855336
です。あまりにも桁数が多いので、10桁ごとに間隔をあけてみました。数えてみるとちょうど70桁の数になり、「63無量大数」 という数になるのです!17×17マスの図はこちらのような図になります。

この図のなかにある道の通り方が無量大数にもなる…少し理解がしにくいかもしれません。
ちなみに京都の道は「碁盤の目」とも呼ばれるほどきれいに道が縦横に伸びています。上の図よりももっと道の数はたくさんあります。
京都の町を同じ道や交差点通らずに歩き回ることを考えたときに、その歩き回り方は無量大数通りを超える、ということなのです…!

無量大数、それは意外と身近なところにある
無量大数がとてつもなく大きい数であることには変わりありませんが、それと同時に大きな数が意外と身近なところにあることご理解いただたでしょうか。
この道の進み方に関する問題は、2018年の時点で26×26マスまでの場合までコンピュータを活用し計算されておりまして、26×26マスの場合は163桁もの道順の組み合わせがあることがわかっています。
もしかしたら近々、27×27マスまでの計算した、という結果がニュースで取り上げられるかもしれませんね。
このような身近な面白い数学・算数の話は『文系もハマる数学』(青春プレイブックス)でも紹介しております!ぜひ、興味がありましたらお読みになって下さい。










