突然ですが、問題です。
10L桶に油が10L入っています。7Lマスと3Lマスを使って、3つの容器で油の移し替えをして、5Lずつ等分するにはどうしたらよいでしょうか。
これは吉田光由(よしだみつよし)の著した『塵劫記』(寛永8年版、1631年)に書かれている由緒ある問題です。単位は皆さんがおなじみのものに変えてあります。
西洋には、13世紀の中頃にはすでにこの種の問題があったといわれており、その後のパズル本でも定番のものです。皆さんの中にも見たことのある人が多いのではないでしょうか。
この問題の解答は、試行錯誤でしか求められないのでしょうか。
いいえ、そんなことはありません。今回は、試行錯誤ではない解き方を紹介します。
解き方を紹介!
このように解くことができます。
- まず、各容器にはどんな状態がありうるのかを考えます。
- 次に、それらの状態の間で移り変われる組み合わせを考えます。
- 最後に、その移り変わりを図に表わして解きます。
では、先ほどの問題を使って、1つずつやってみましょう。
①まず、各容器にはどんな状態がありうるのかを考える
使える容器は、10L桶、7Lマス、3Lマスの3つです。
何回か移し替えて容器に入っている油の量を変化させ、7Lマスに5L、10L桶にも5L入っているようにすればよいわけです。
わかりやすくするため、容器に入っている油の量の表し方を決めましょう。
容器は3つありますが、7Lマスと3Lマスに入っている油の量が決まれば、10L桶の油の量も決まります。
従って、7Lマス、3Lマスの入っている油の量の表し方を決めればよいことが分かります。
これをシンプルに、
(7Lマスの油量,3Lマスの油量)
とし、これを“マスの状態”と呼ぶことにしましょう。
例えば、
(7,3): 7Lマスと3Lマスが両方とも満杯、10L桶は空の状態
(5,3): 7Lマスに5L、3Lマスに3L、10L桶に2L入っている状態
“マスの状態”を考えてみると以下のようになります。
- 各マスに入る油の量は、0L以上で満杯量(7Lあるいは3L)以下に限定されます。
- 各マスに入る油の量は整数値です。(樽とマスの間の移し替えは、量の足し算や引き算だけですから、何回繰り返しても整数以外にはなりえません。)
- 7Lマス、3Lマスのうち、少なくともひとつは「空」か「満杯」でなければなりません。(どちらかのマスが空になるか満杯になるかまで油を移し替えるためです。)
以上から取り得る “マスの状態” は、以下の20通りに絞られます。

②次に、それらの状態の間で移り変われる組み合わせを考える
次に、ある“マスの状態”から移り変わることのできる(遷移可能な)“マスの状態”の組み合わせを考えましょう。
例えば、(0, 0) という状態から遷移可能な状態を考えると、(7, 0)、(0, 3)の2つがあることが分かります。状態(7, 3)からも、(7, 0)、(0, 3)の2つに遷移可能です。この遷移は逆方向も可能です。
このような遷移を双方向の遷移ということにします。
双方向の遷移をもう少し分析してみましょう。次のような遷移があることに気づきます。
- 3Lマスが空の状態 ⇔ 10L桶から3Lマスに油を注ぎ、3Lマスが満杯の状態
- 7Lマスが空の状態 ⇔ 10L桶から7Lマスに油を注ぎ、7Lマスが満杯の状態
- 3Lマスに余裕のある状態 ⇔ 7Lマスから3Lマスに油を移した状態
- 7Lマスに余裕のある状態 ⇔ 3Lマスから7Lマスに油を移した状態
①は、「3Lマスが空の状態なら、7Lマスに入っている量には無関係に、3Lマスに3L注ぐことができます。逆に3Lマスが満杯の状態なら、7Lマスに入っている量には無関係に、3Lマスを空にすることができます」ということがいえます。
つまり、以下の組み合わせがあります。
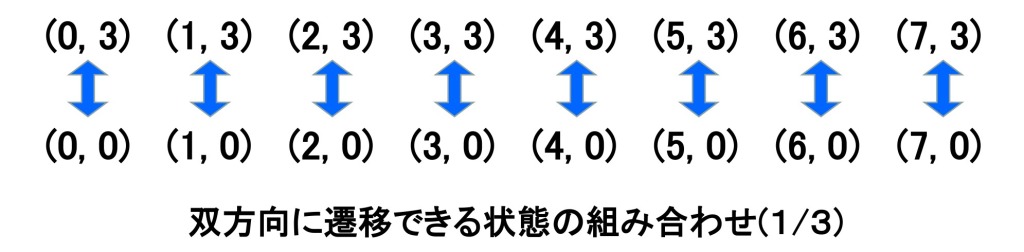
同じように、②は、「7Lマスが空の状態なら、3Lマスに入っている量には無関係に、7Lマスに7L注ぐことができます。逆に7Lマスが満杯の状態なら、3Lマスに入っている量には無関係に、7Lマスを空にすることができます」ということです。対応する組み合わせは以下のようになります。

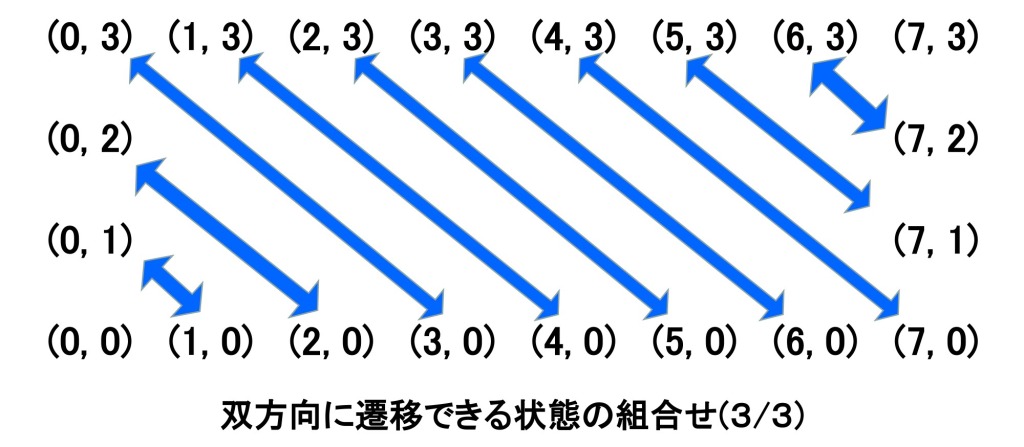
③④に対応する組み合わせは少しややこしいですが、下のようになります。
矢印の上側が7Lマスから3Lマスに油を移した状態(③)、矢印の下側が3Lマスから7Lマスに油を移した状態(④)です。
③最後に、その移り変わりを図に表わして解く
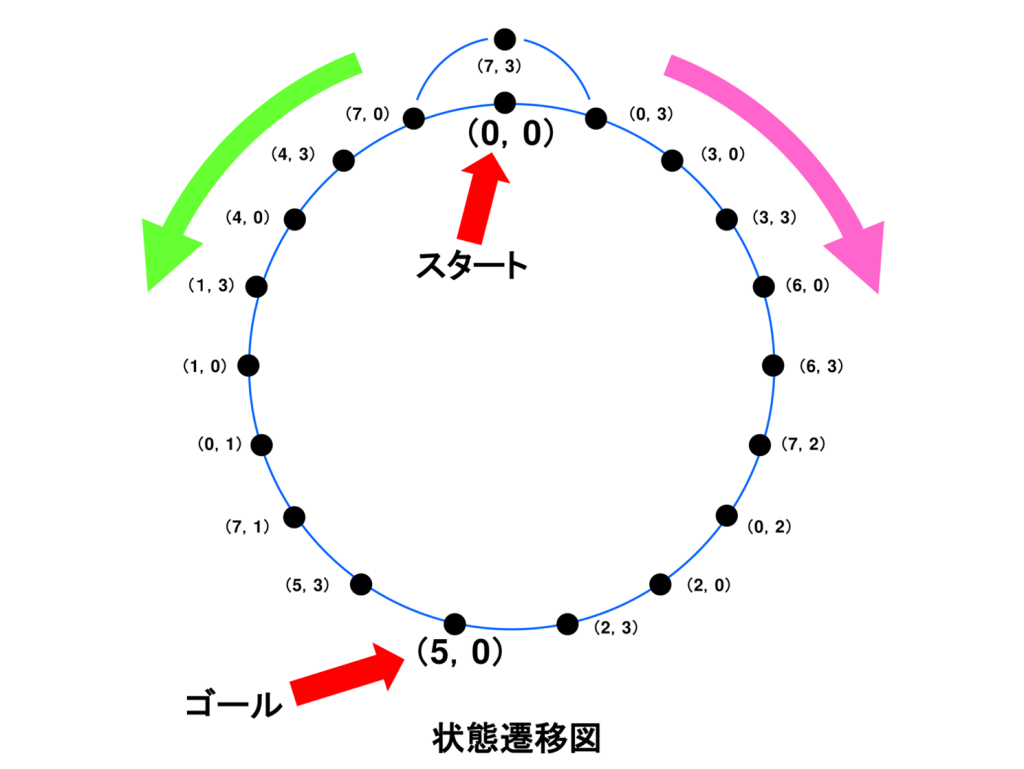
以上のことを考慮しつつ丹念に状態遷移をまとめると、下の図のようになります。
各状態の遷移関係を青線で表現しています。このような図を状態遷移図といいます。
実は、上記以外にも、片方向の遷移が存在します。
例えば、(0,1)から(0,0)あるいは(0,3)に遷移するルートです。
しかし、このようなルートは、状態遷移図で明らかなように、スタート近辺に戻ることになるので、このパズルでは、考慮する必要はありません。
答えまであと少し!
この状態遷移図を使えば油分け算は簡単に解くことができます。
状態(0,0)のスタートからゴールの(5,0)までは、左回り(反時計回り、緑色)でも右回り(時計回り、ピンク)でも到達できますが、左回りの方が1ステップ少なくなります。左回りに進む場合の答えを以下に示します。
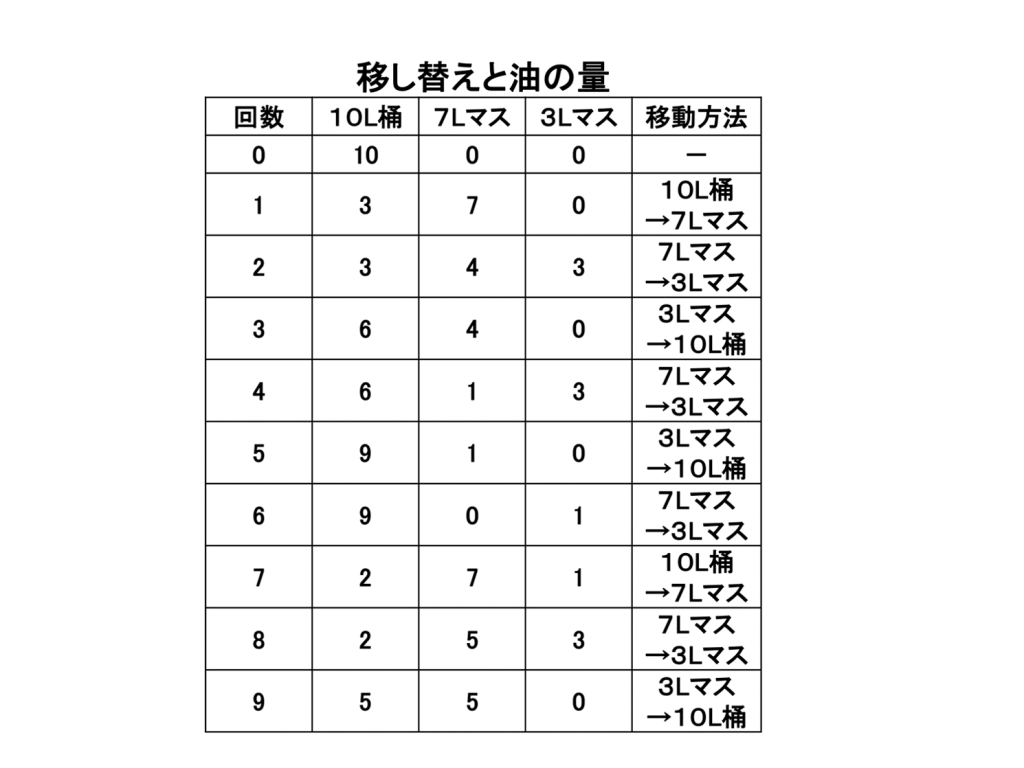
今回ご紹介した方法は1939年、M.C.K.ツイーディーが発表した図を用いた巧妙な方法と基本的に同じです。
興味のある方は調べてみてください。
終わりにー状態遷移図の学問的背景
今回ご紹介した状態遷移図の学問的背景を少し説明します。
情報科学の用語としての状態遷移図とは、ある状態がある動作によって、どのような状態に移り変わるか、ということを図面化して見やすくしたものです。
ソフトウェアや各種システムの仕様を正確に定義する方法として設計によく用いられています。
下に示した例は、エレベーターに乗り、行きたい階(目的階)のボタンを押した際のエレベーターの制御です。停止中、上昇中、下降中が状態で、油分け算の(7Lマスの油量,3Lマスの油量)に対応しています。
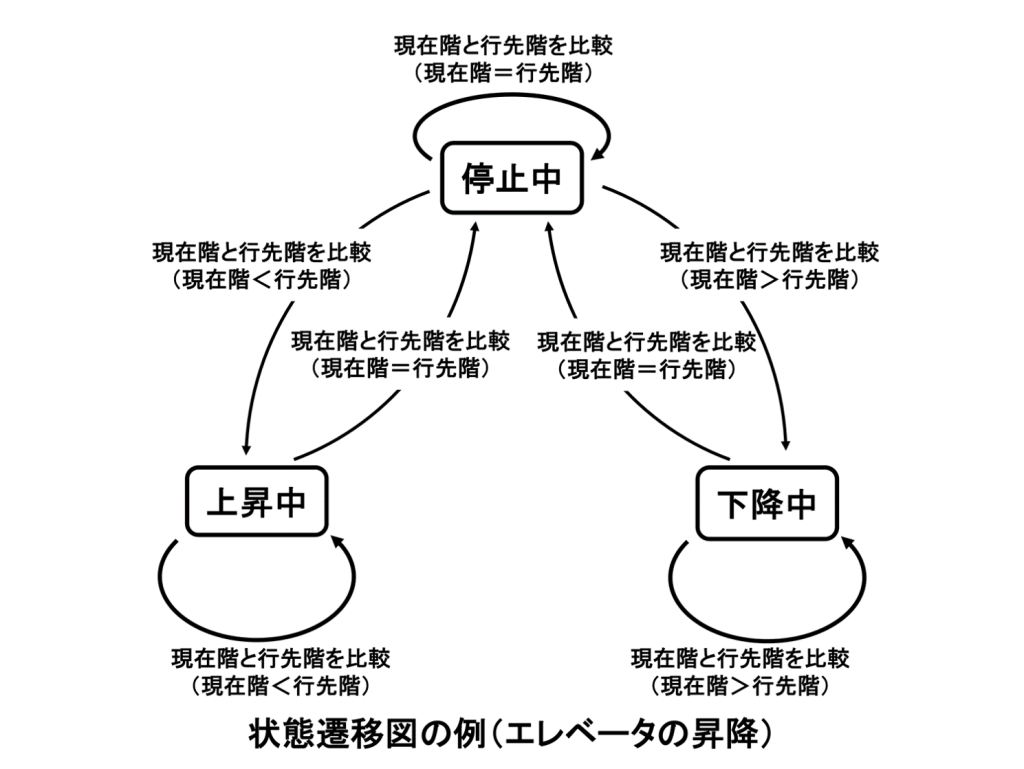
プログラミングを学ぶ機会も多いかと思います。正しいプログラムを書く上で状態遷移図は非常に有効な手段です。
是非、今回の方法を使ってみると、いつもと違ったプログラミングができるかもしれません。