中学入試の算数指導歴30年 滝澤です。
2023年の中学受験が、2月にほぼ終わりました。苦しい時を乗り越え,目標に向かって一生懸命戦ったすべての小学6年生のみなさん、そして保護者のみなさん、塾や中学校の先生方、お疲れ様でした。
先日、筑駒中と開成中などに合格した6年生が遊びにきてくれました。
彼は昨年の9月に初めて解いた開成の過去問演習でなんと85点満点中7点でした。さらに12月中旬にもスランプに陥り、志望校を下げようかとも悩んだそうです。
ですが、地道に問題演習を繰り返すことで自信をつけ、見事合格することができました。
スランプを乗り越えるために必要なことは、やはり問題を解くことを「面白い!」「楽しい!」と思えるか否かです。
正解不正解はともかく、算数の問題を考えること自体が楽しければ、自然に問題演習量も増え、力もつきます。
面白い問題に出会うことはとても大事なのです。
さて、今年も多くの算数の面白い問題に出会うことができました。今回はその中でも、有名中学の出題の中から面白い問題ベスト3を選んでみたいと思います。
面白い問題とは
私なりの「面白い」の判断基準ですが、
- 小4・小5でもチャレンジできる単元・難易度のもの
- 解法の知識などがなくても試行錯誤をくり返した末に答えを導き出せるもの
- 手間がかかりそうだけど,工夫によって簡単に解けるもの
などが挙げられます。
ではさっそく、第3位から参りましょう。
第3位 灘中学 1日目 大問3
1桁(けた)の数A、2桁の数BC、3桁の数DEFと
3桁の数ABC、2桁の数DE、1桁の数Fについて、
A+BC+DEF=ABC+DE+F
が成り立っています。このとき、次のアからソのうち必ず成り立つものは
3つあります。それは(① )と(② )と(③ )です。
ただし、①、②、③の順序は問いません。
ア A=B イ A=C ウ A=D エ A=E オ A=F
カ B=C キ B=D ク B=E ケ B=F コ C=D
サ C=E シ C=F ス D=E セ D=F ソ E=F
Takizawa’s check
灘中といえば、日本でも1、2を争う最難関校です。算数の問題も難問が多く出題されます。
しかしこの問題は比較的簡単な問題ですから、挑戦していただきたい問題です。
例えば、「692」という数字は、「六百九十二」という意味だということはたいていの小学生でもわかります。つまり、692=6×100+9×10+2×1だということがわかっているわけです。
この問題では数字の代わりにアルファベットが使われていますが、同じことですね。ABCはA×100+B×10+C×1です。このことがわかれば小4・小5でもチャレンジできるかもしれません。
【解説】
A×1+B×10+C×1+D×100+E×10+F×1=A×100+B×10+C×1+D×10+E×1+F×1
=の左右両方に「B×10」、「C×1」、「F×1」があるからこれらを取り除くと
A×1+D×100+E×10=A×100+D×10+E×1
よって、3けたの数字に直すと DEA=ADE
各位がそれぞれ等しいから、A=D、A=E、D=E となる。 答 ウ、エ、ス
第2位 札幌日大中A日程 大問5
病気の診断のための検査はにはいろいろな方法があります。検査を受けたとき、その結果から、陽性(病気である)か陰性(病気でない)と判断されます。病気であれば100%陽性、病気でなければ100%陰性と判断される検査が理想ですが、理論上100%にすることは不可能なので、病気であっても陰性になったり、病気でなくても陽性になったりします。
どんな検査にも「感度」と「特異度」というものがあります。「感度」とは、病気である人を陽性と判断する割合を、「特異度」とは、病気でない人を陰性と判断する割合を表します。例えば、感度は90%の検査では、病気である人を100人検査すると、90人は陽性と判断されますが、10人は陰性と判断されるということです。
ある病気について、感度が70%、特異度が99%である検査を日本在住の1億2000万人に行います。病気である人は日本在住の0.1%であるとし、次の問いに答えなさい。
問1 病気である人は何人いますか。億や万などの漢数字を使わずに答えなさい。
問2 この検査で陽性と判断された人のうち、病気である人の割合は何%ですか。四捨五入して小数第1位まで答えなさい。
Takizawa’s check
社会の入試問題では、時事問題と言われる問題がよく出題されます。これはその年にあったニュースや出来事などから出題されるわけですが、算数でも時事問題が出題されることがあります。
ニュースを読んでいると新型コロナのニュースで、このような検査の精度について話題になることもあります。「感度」や「特異度」という言葉も聞いたことがあるかもしれませんね。しかし、これを試しに計算してみようと思った小学生はなかなかいなかったのではないでしょうか。
【解説】
問1 12000万人×0.001=12万人=120000人 答 120000人
問2 健康な人は、12000万人-12万人=11988万人
特異度が99%だから、健康な人のうち陽性になった人は、 11988万×0.01=119.88万人
病気である人は12万人で、感度が70%だから、病気である人のうち陽性になった人は
12万人×0.7=8.4万人
よって 8.4÷(8.4+119.88)=0.065481……=6.5%
解き方自体は小5で習う割合と百分率の基本問題ですが、言葉に慣れないとなかなか解きづらいのではないかと思われます。
ちなみに、このような値(陽性と判断された人のうち、病気である人の割合)のことを陽性的中率といいます。
陽性的中率は、有病率(病気である人が全体で何%いるか)によって大きく左右されます。
算数の時事問題と言えば、他に選挙や消費税など、政治や社会にまつわる問題から出題されることもあります。
今年の灘中では架空の円と通貨「ナダ」の為替に関する問題が出題されました。
ニュースをただ読むだけではなく、数字が絡む問題である場合は、どんな計算方法なんだろう?と調べてみたり、質問したりする気持ちを持てるとよいですね。
第1位 筑波大附属駒場中 大問2
次の図1または図2のマスに、0から9までの数を1つずつ書くことを考えます。
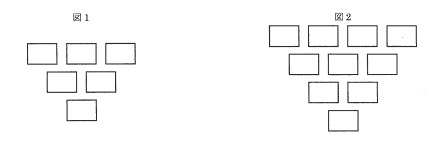
図のマスに数を書く<きまり>は次の通りです。
| <きまり> ① はじめに、3けたの整数、または4けたの整数を1けたずつに分けて、 図の一番上のマスに書きこむ。3けたのときは図1を、4けたのときは図2を使う。 ② 同じ段の、となりあう左右2つのマスに書かれた数のうち、大きい数から小さい数を ひき、その結果 を2つのマスのすぐ下のマスに書く。 ただし、2つのマスの数が同じときは0を書く。 ③ 図の一番下の段のマスに数が書かれるまで、②をくり返す。 例えば、次のようにはじめの整数が2023のとき<きまり>にしたがって最後に書かれる数は1です。 |
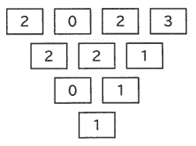
次の問いに答えなさい。
(1)~(2) 略
(3) 100から999までの900個の整数のうち、<きまり>にしたがって最後に書かれる数が8であるものは何個ありますか。
(4) 1000~9999までの9000個の整数のうち、<きまり>にしたがって最後に書かれる数が8であるものは何個ありますか。
Takizawa’s check
使う知識はひき算だけ。ルールにしたがって数をうめていく問題ですから、小4小5でも挑戦できますね。
ただし、ひき算の答えを求めるのではなく、ひき算の式を考えるという逆に考えていくことと、もれなくしっかり書き上げることを求められていますから、完全に正解するのは難しいかもしれません。
いったいいくつ見つけられるかな?みたいな気持ちで取り組んでみると楽しいと思います。
【解説】
(3)1番下の数が8になるためには、その上の2けたが「08」、「19」、「80」、「91」にならなければいけない。その上の3けたの数をていねいに考えればよい。
「08」の上→119、880、991
「19」の上→109、890
「80」の上→199、800、911
「91」の上→901 答 9個
(4) (3)の答え3けたの数の上にある4けたの数をていねいに考えれば次の19個が見つかる。
1009、1090、1900、1911、1999、2109、7890、8000、8088、8099、8909、8990、9001、9010、9012、9098、9111、9199、9890
しかし(3)では答えにならなかった008,088,098の上にある4けたの数が7個ある。
1191、8808、9919、1119、8880、9991、9908 答 26個
いかがだったでしようか。まだまだこれ以外にも楽しめる問題が多くの中学で出題されています。
気になる方は、「2023 中学受験 算数 問題」などで検索するか、または四谷大塚さんの過去問データベースに登録して気になる中学校の入試問題をのぞいてみるのもおススメです。
他の中学受験の問題にも取り組んでみよう!
中学受験算数の取り組み方は連載で紹介中!
タッキー先生が中学受験算数の参考書を徹底解説!
(文責:滝澤 幹)