こんにちは。中学受験算数ナビゲーターの滝澤です。
前回は時計という身近なものを使っていかに想像力を広げ、時間とともに変化する様子をとらえられるかといった問題をご紹介しました。
さて今回は同じく身近なものを利用して、時間的な想像力ではなく、空間的な想像力を駆使する問題をご紹介します。
問題です。/灘中学(2017年、2日目 算数の問題(1))
2017年 灘中学 2日目 算数の問題(1)図形問題
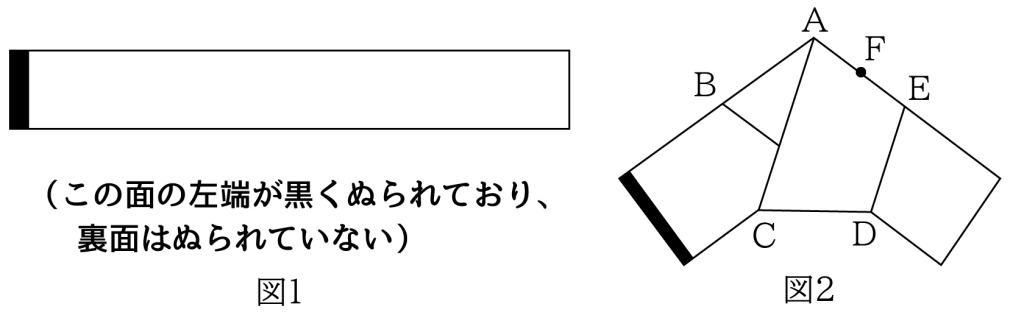
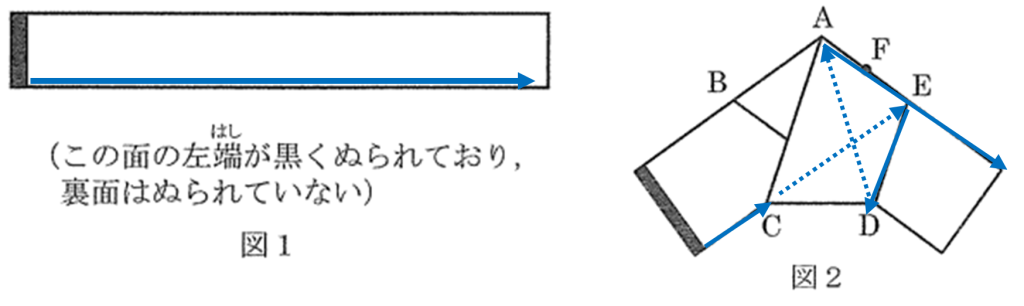
図1のような長方形の細長い紙を3つので折り込み,図2のようにしました。5個の点A,B,C,D,Eを頂点にする五角形は正五角形です。また,点FはAEの真ん中の点です。
図1のような長方形の細長い紙を3つの折り目で折り込み、図2のようにしました。5個の点A、B、C、D、Eを頂点にする五角形は正五角形です。また、点FはAEの真ん中の点です。
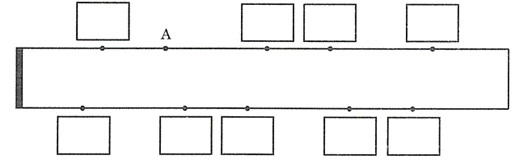
(1) 紙を折り込むと,下の図のすべての黒点は図2の点A,B,C,D,Eのどれかの位置に来ます。9か所の空欄にA,B,C,D,Eのうち,あてはまるものを記入しなさい。
(2) 図2の紙を直線CFに沿ってはさみで切るとき,切り口を下の図にかき込みなさい。なお,下の図の黒点は(1)の図と同じ位置にあります。

身近なものを思い出そう。
いかがでしょうか。この図を見ると、何かを思い出しませんか。
そう。割り箸の袋ですね。
とはいっても、最近では割り箸の袋を実際に目にすることは少なくなりました。割り箸そのものが少なくなりましたし、コンビニなどではブラスチックの袋に入っていることが多いですね。
このような形の長方形を結ぶように折り込んで五角形を作る遊びは、今の子どもたちは経験がないかもしれません。

図形問題は、触感のイメージが重要
では、どのように想像していけばよいのでしょうか。
図形が折り込まれていくのを視覚的に想像するだけではこの問題は大変難しいように思われます。紙を手で触って、手で折ってと触感のイメージが大切なのではないでしょうか。
つまりこの問題では、長方形の上辺、下辺をそれぞれ指でなぞっていくとどうなるのか、というイメージがあると解きやすくなります。
それでは解説にいきましょう。
解説です。
まずは(1)。順に頂点を読んでいこう
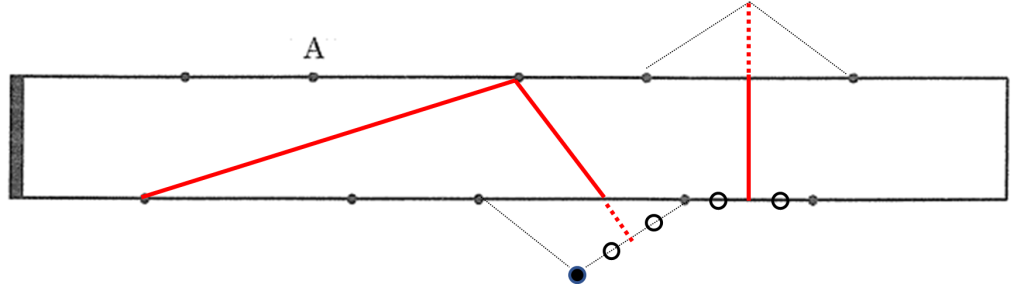
(1) 図1の長方形の上の辺にそって左から順に図2の図を見ていくと下の赤い矢印のようになります。(点線は紙の裏側を通っています)この順に頂点を読んでいくと B、A、C、B、Dとなります。
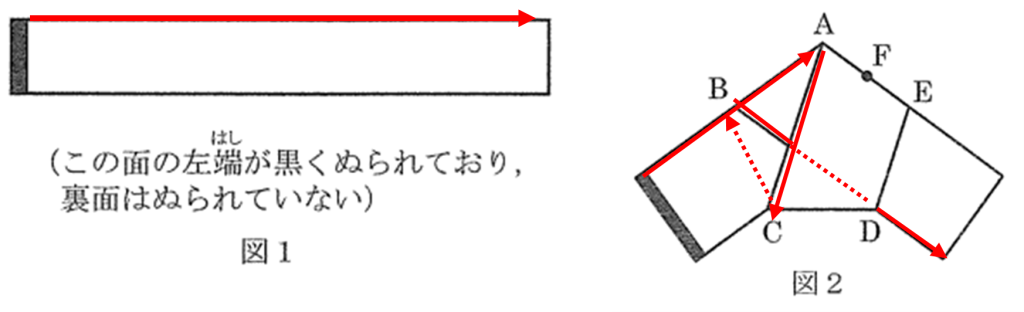
次に長方形の下の辺にそって左から順に図2の図を見ていくと下の青い矢印のようになります。この順に頂点を読んでいくと、C、E、D、A、Eとなります。
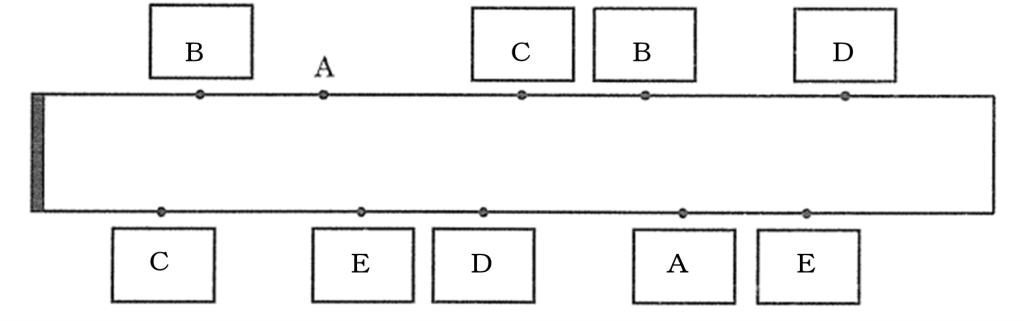
よって解答は下のようになります。
もし想像しづらければ、実際に細長い紙をさわりながらやってみることをおすすめします。
続いて(2)は、よくある間違いに注意!
では(2)にすすみましょう。CFに線をひくと,次のようになりますね。この長方形の紙を元に戻すとどのように切れ目が入るかということですが、(1)の答えを利用して考えてみましょう。
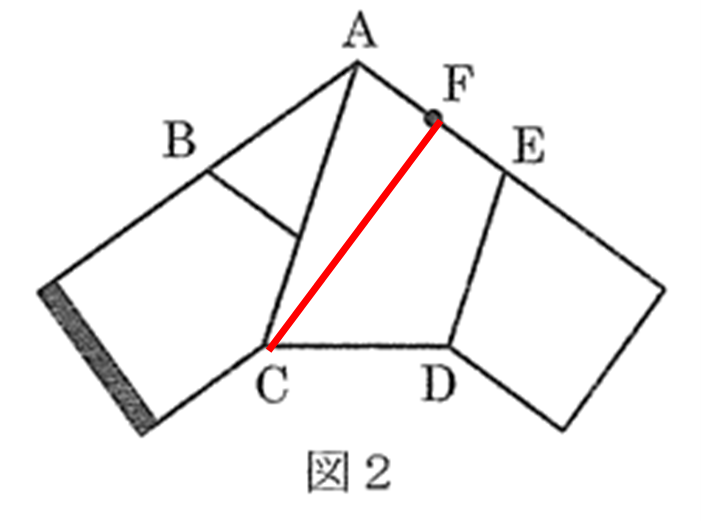
まずは(1)の解答に点Fを書き込みます。点Fは点Aと点Eのちょうどまん中ですから、下の図のようになりますね。
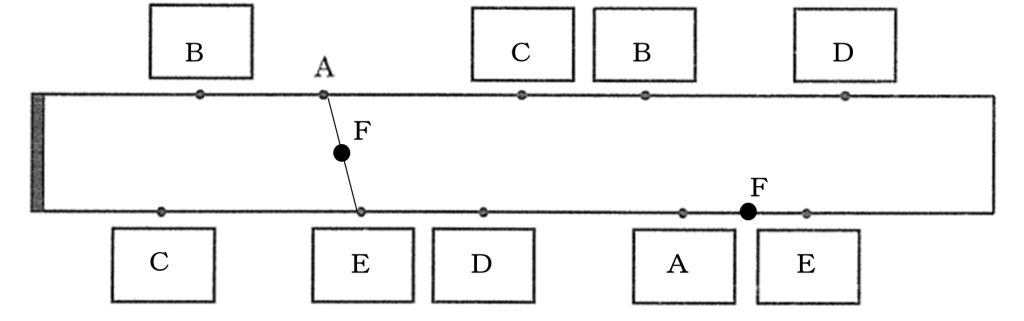
この状態から、CとFを結べばよいので一瞬こうなるように思います。
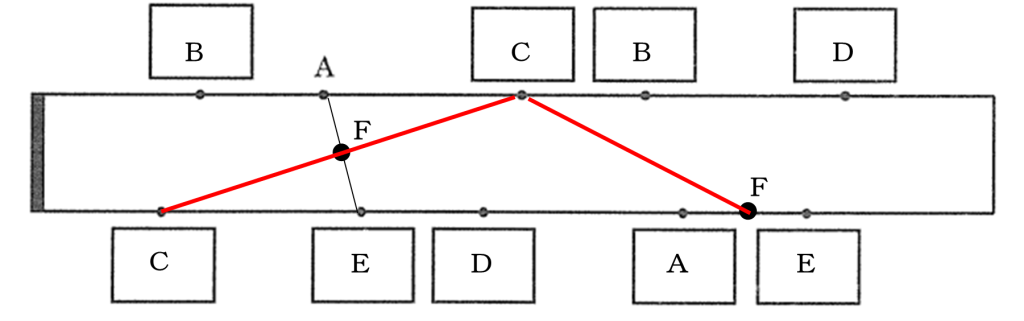
が、これはよくある間違いです。
見えているものだけをただ結んでみただけですね。この問題は五角形の頂点と、対辺の中点の結ぶという問題なので、常に五角形を考えておかなければ解くことができません。
開いて長方形にしてしまうと消えてしまう五角形を想像で補完して考えなければいけないということです。
実際にどのような図をかいて考えればよいのでしょうか。
まずAとE、CとD、BとA、DとEを結びましょう。すると長方形に台形が4つできます。
この台形は、それぞれ別の正五角形の一部になります。
よって、それぞれの台形が含まれる正五角形をこの図に書き込んでいきます。この正五角形1つにつき、1本切れ目が入るはずなのです。
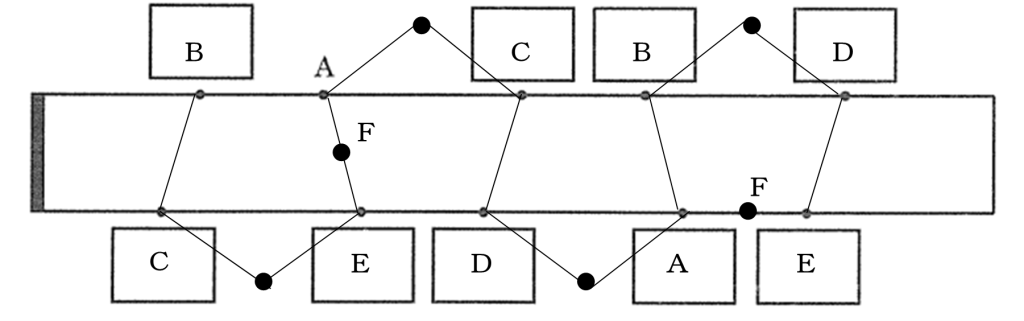
この図に正五角形の5つの頂点はすべて、点A、点B、点C、点D、点Eなので、頂点の名前もしっかり書き込みましょう。
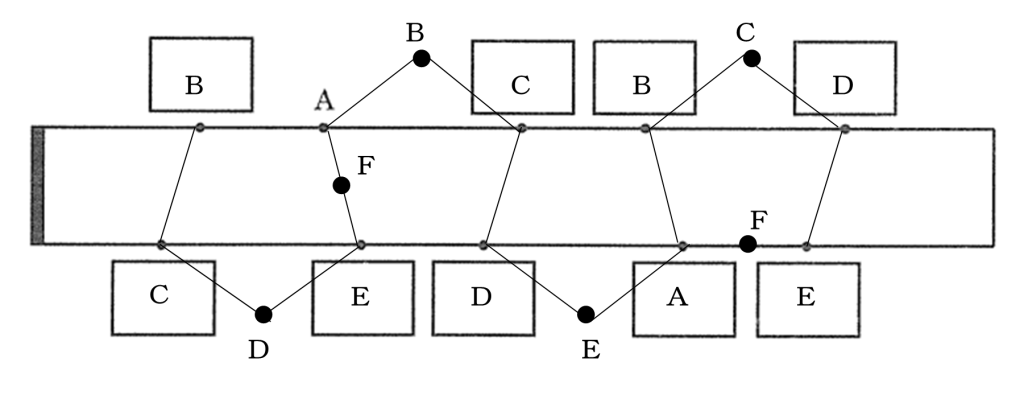
さらにここにAEのまん中の点である点Fを書き加え、CとFを結ぶと答に限りなく近づきます。
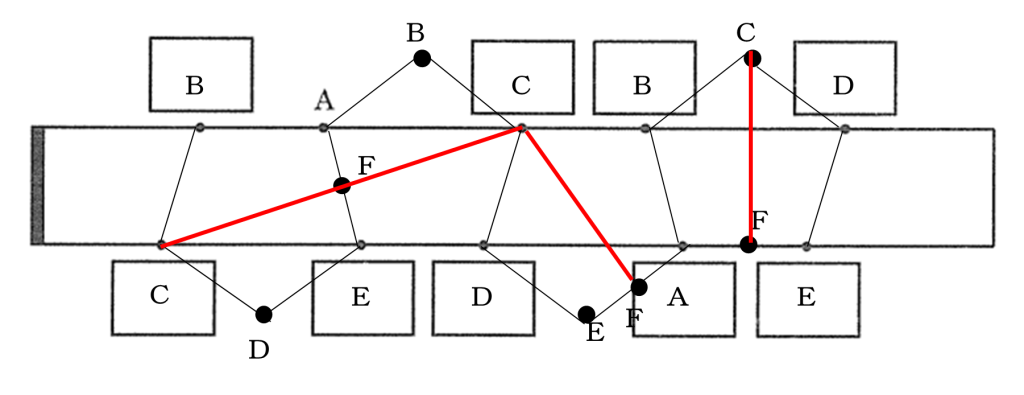
実際には、答えには長方形しかありませんから、このような線をかくと正解になります。
作図問題の注意点
この問題の解答のように、点と点を結ぶのではなく、中途半端な位置から線をひくばあいは、2つの点の中点であることや線分比を書き込んでおくほうがよいと思われます。
また、点線などでどのように考えて作図をしているかを表したほうが伝わりやすくなります。これは作図だけに限りませんが、答案はいかに採点者に伝わるかを意識して書くとよいでしょう。
ノートに解くだけが勉強ではありません。
この問題も、実際に細長い紙を折った上で、実際にはさみで切ってみることをおすすめします。
紙を折ったあとに切って広げる問題は、多くの中学校で出題されますが、あくまでも想像すべきなのは、自分が手を動かして折って、切って、開いているイメージです。そのためには紙をつかって実際に経験することが大切です。
想像力の源はあくまでも実際の経験なのです。
このような問題にめぐりあったときは、ぜひ紙とえんぴつで書くだけでおわらせず実際に作ってみることをおすすめします。
数学になると、このように実際にものをさわって考える経験はどんどん少なくなっていきます。空間的なイメージを育てる体験は、算数でこそ身につけられる大切な勉強なのです。
さて、次回は 海城中学の相似の問題です
相似の問題はオーソドックスな解き方がいろいろありますが、たまには裏技をお見せしましょう。お楽しみに。
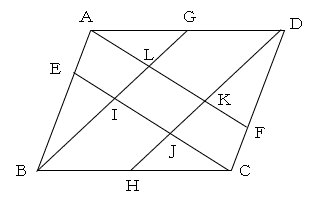
問題
下の図のように,平行四辺形ABCDの辺ABを1:2に分ける点をE,辺CDを1:2に分ける点Fとし,辺BCを辺DAの真ん中の点をそれぞれG,Hとします。また,BHとCEが交わる点をI,CEとDGが交わる点をJ,DGとAFが交わる点をK,AFとBHが交わる点をLとします。次の問いに答えなさい。
(1) BI:IL:LHを最も簡単な整数の比で答えなさい。
(2) 平行四辺形ABCDと四角形IJKLの面積の比を最も簡単な整数の比で答えなさい。
(3) 平行四辺形ABCDと四角形AEILの面積の比を最も簡単な整数の比で答えなさい。