子どもに対して「算数を楽しく学んでほしい」と思う方は多いはずです。
しかし、自分自身「算数の楽しさがどこにあるかうまく説明できない」「結局は正解できれば楽しいかもしれないけど、間違えたら楽しくない」と悩み、うまく子どもに働きかけられないという方もいらっしゃるのではないのでしょうか。
今回は 、 開成中の入試問題の中から平面図形の問題を題材に、算数を楽しむポイントを「1つ」紹介できればと思います。
算数とは「同じもの探し」
算数の考え方の大きな1つの柱は、2つの数をくらべることにあります。
とりわけ「どれとどれが同じか?」はとても大事な考えの源です。
算数の問題で「式」と「答え」を書きますが、式とは、多くは等式のこと。これは、「=」の右側と左側が同じであるということを示しています。
要するに算数とは、「同じもの探し」をする勉強なんだということが言えると思います。
算数の面白さの1つには、「これとこれが同じなの!?」という意外性の発見をする楽しさがあります。
図形で言えば、見逃しがちな同じ長さや同じ角度などを見つけたり、自分で補助線を描くことによって同じものをつくったりすることができるととても楽しいのです。
そして、面積の問題でも、全く形が違うのに同じ面積の形が見つけることができると、とてもうれしくなります。
今回は、この切り口から、開成中の2015年の平面図形の問題を紹介したいと思います。

その問題は、こちら
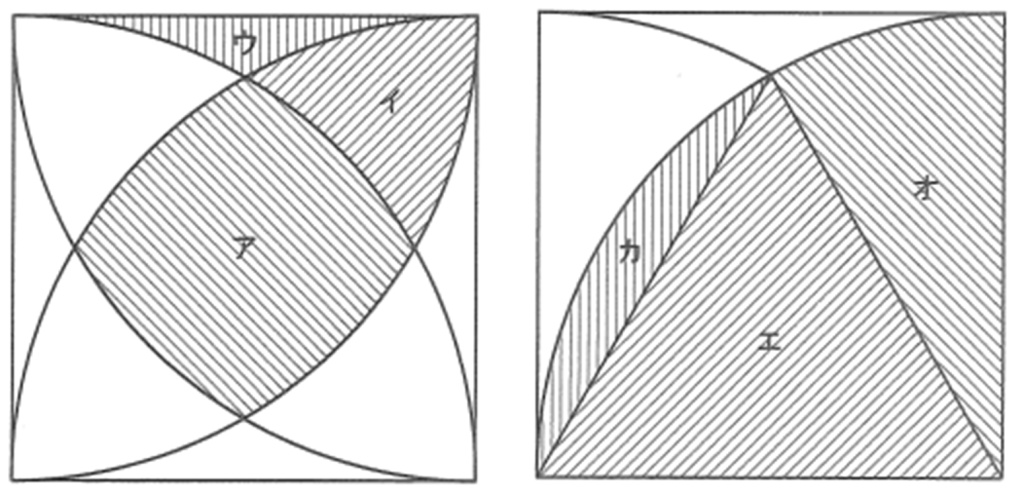
同じ大きさの正方形を直線や円で区切って、図のように図形、ア、イ、ウ、エ、オ、カをつくりました。そしてアの面積をア、イの面積をイ、ウの面積をウ、エの面積をエ、オの面積をオ、カの面積をカと表し、正方形1つ分の面積をキで表すことにします。これらの面積には、例えば
キ=ア×1+イ×4+ウ×4
のような関係があります。
その他に、次のような関係を見つけました。サ~ツにあてはまる整数や記号を答えなさい。
セには記号ア~キのどれかがあてはまり、その他には整数があてはまります。
(1) カ=オ×サ-エ×1
(2) ア+イ=オ×シ-エ×ス
(3) イ+ウ+オ=セ
面白さはココだ!
いかがでしょうか。
まずは問題の式をよくながめてみると、(3)の式が特徴的なものになっています。
この式は、イとウとオを足したら、ア~キのどれかになる、ということを表しています。一見バラバラな図形どうしが組み合わさってほかの図形になる……少し不思議で、少し楽しくありませんか?
ちなみに、イとウとオには絶対なりません(なりませんよね?)から、アかエかカかキ(キは全体の正方形)になるということですよね。
でもさすがにカは小さすぎるし、キは大きすぎる。
ということはアかエ?
イとウとオを足すと、アかエになるの?
そんなことってあるのでしょうか?
とワクワクしながら、解いていきましょう。
(3)を解くためには、(1)と(2)をクリアしなければいけません。そういうものです。
(1)と(2)は比較的簡単に解ける、はず、なので頑張りましょう。
同じ長さに印をつけよう ~(1)の解説~
図形の問題はまず大切なのは、同じもの探しです。同じ長さには同じ印をつけていきましょう。
そしてどんな形や大きさが見えるかが大事です。
形の名前や角度の大きさなども考えながら見ていきます。
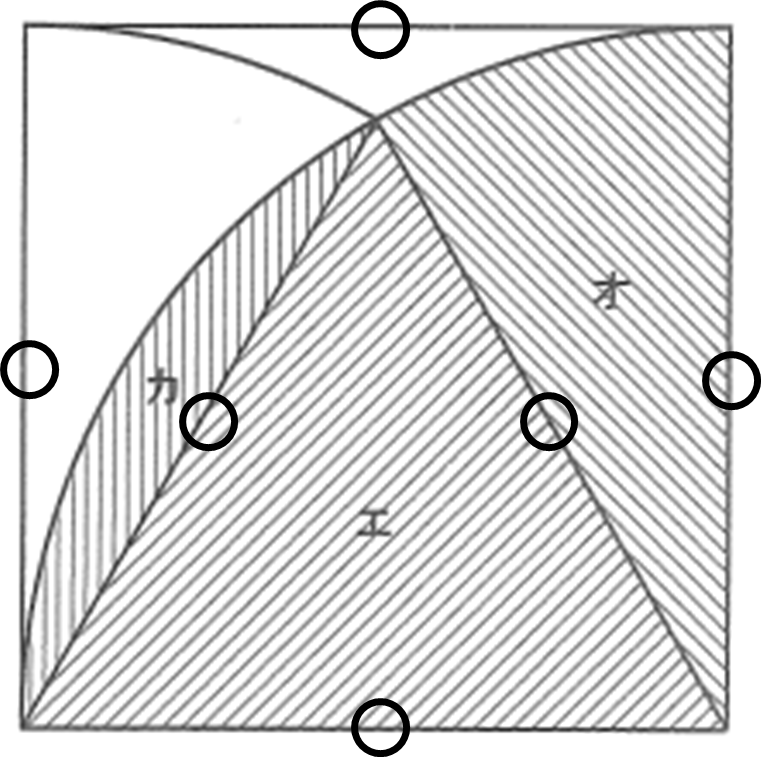
というわけで、エは正三角形であることがわかりますね。
正三角形の1つの角度は60°ですから、オのおうぎ形の中心角は30°ですね。
さらに、エとカを合わせた形は中心角が60°のおうぎ形であるのが見えますか?
これオのおうぎ形のちょうど2倍の面積ですよね。これがわかれば、(1)のサにどんな整数が入るかはわかります。
カはオのサ倍からエをひいたものです。という式ですから、サは2ですね。
補助線のひき方(基本) ~(2)の解説~
(2)を考えるときには、補助線をひくとわかりやすくなります。
補助線のひき方がわからないという質問をたまに頂くことがありますが、基本は「交点と交点を結び、作りたい形ができるように線をひく」です。
では実際にやってみましょう。
交点とは、線と線が交わってできた点のことです。
(2)はア+イについて聞かれていますから、アとイのあたりの交点は下の図の●のついたところになります。
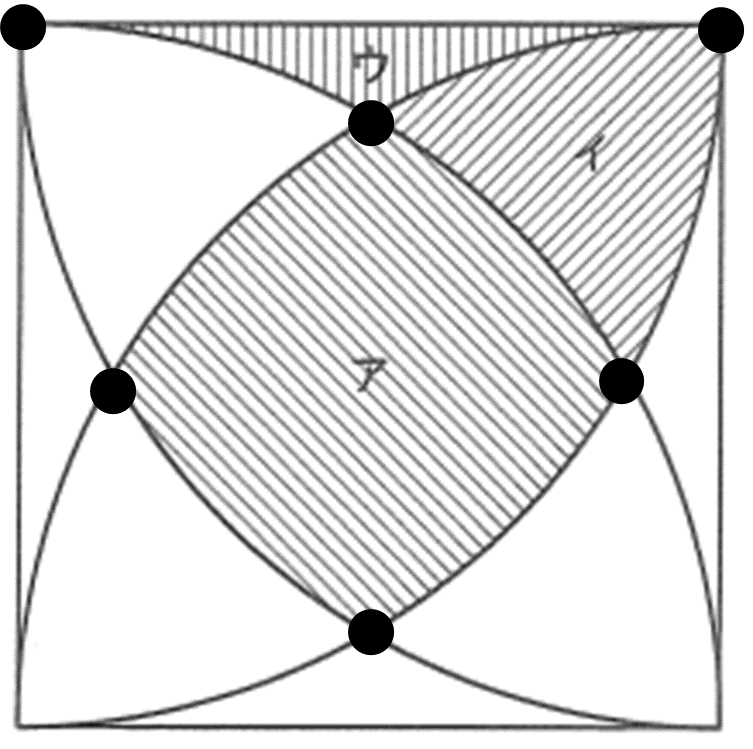
この5つ点のうちいくつかを結んで、どんな形を作ればよいのでしょうか?
これはもちろん、エ、オ、カなどが作れればよいですよね。ということで、
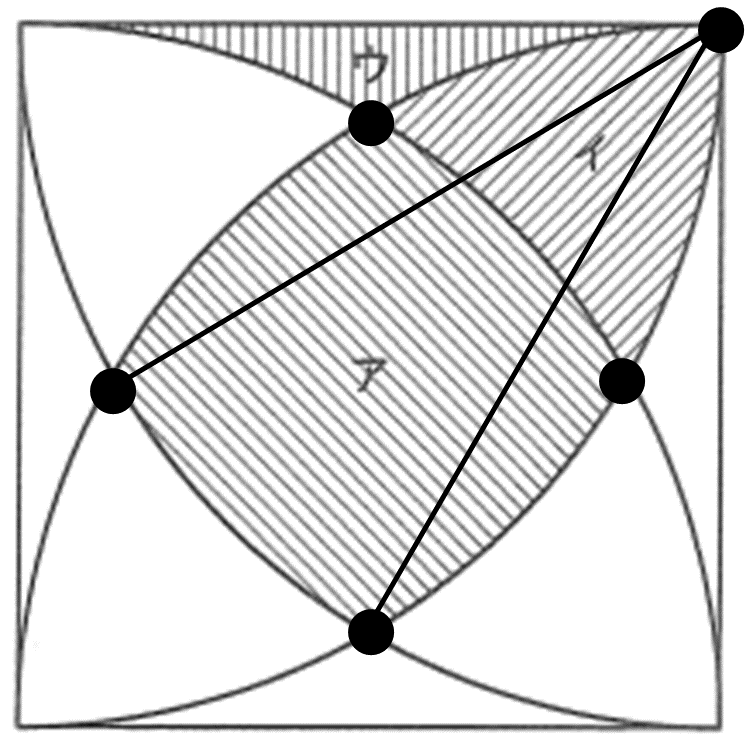
このようにひいてみると、
ア+イ=オ+カ+カ
であることがわかります。そしてカについては(1)で
カ=オ×2-エ×1
であるとわかっていますから、
ア+イ=オ+オ×2-エ×1+オ×2-エ×1
となり、
ア+イ=オ×5-エ×2
つまりシが5、スが2ということがわかります。
やはり補助線は最強 ~(3)の解説~
さあいよいよ(3)です。
イとウとオを足すということは,図形として考えるとならべるということです。
補助線をひいてイとウとオを並べてみましょう。
(2)でひいた補助線がヒントになります。
今度は補助線がイを横切らないないように補助線を2本ひいて、イとウとオがならぶようにすると、すきまがちょうどカになります。
これを問題の右側の図と見比べるとイ+ウ+オ+カはちょうど中心角が60°のおうぎ形になり,エ+カも同じですね。
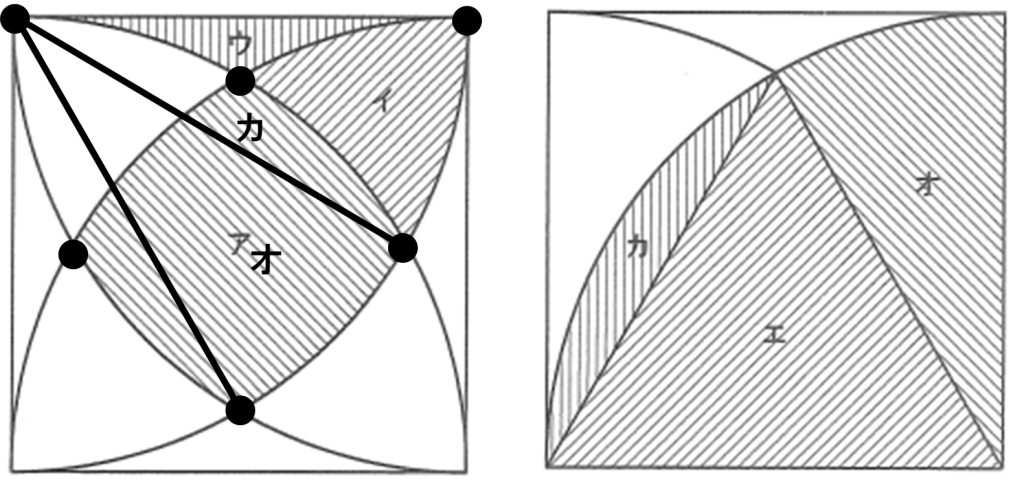
つまり,
イ+ウ+オ+カ=エ+カ
となるわけです。
よって,
イ+ウ+オ=エ
になりますね。
おうぎ形や曲線と直線に囲まれた図形をいくつかたすと正三角形になるのですね。実際に紙を切ってならべて試してみるのもいいかもしれません。
いろいろな楽しみ方を見つけられる力が一番大切
算数の問題の楽しみ方ということで、図形の形に着目して開成中の問題とその解き方を紹介してきました。
これは算数の話に限らないかもしれませんが、「楽しむ」といってもまずは楽しみ方を見つけなければいけませんよね。
様々なことにそれぞれの楽しみ方があって、それらの楽しみ方を1つでも多く知っていたり見つけられたりする力があれば、算数はもちろん、他の様々なことに興味が持てて充実した生活が送れるのではないかと思います。
算数で必要な力はたくさんあります。
集中力、発想力、情報処理力、表現力、検証力、戦略的思考力、地道力、想像力などなど。
それらの根本となるのは、楽しみ方を見つけられる力なのだと思います。
おまけ
※実はこの問題は(4)の問題もあります。
(4) ア=キ×1+オ×ソ-エ×タ
イ=エ×チ+オ×1-キ×1
ウ=キ×1-エ×1-オ×ツ
の、タ、チ、ツに入る数字を求めるという問題です。ぜひ、挑戦してみてください!
(文責:滝澤幹)









