頭脳パズル「偽物の金貨」応用編！3の倍数ではない枚数の場合は、どう見つける？わかりやすく解説します【後編】

こんにちは、みうらです。

前回は、金貨の枚数が 3^k　（3、9、27、…）の形をしている場合について解法をお話ししました。
この場合、金貨を3分の1ずつに分割し、天秤で「軽い」「重い」「等しい」という3つの結果を得ることで、1回、2回、3回、…の測定回数で偽物を特定できることを示しました。

今回は、このアイデアを踏まえ、金貨の枚数が 3 ^k の形ではない場合について、効率よく偽物を特定する方法を探っていきましょう。

4枚から8枚の場合は

まずは、4枚から8枚の場合を考えてみましょう。

唐突ですが、金貨を下の表のように3つのグループA、B、Cに分けます。　

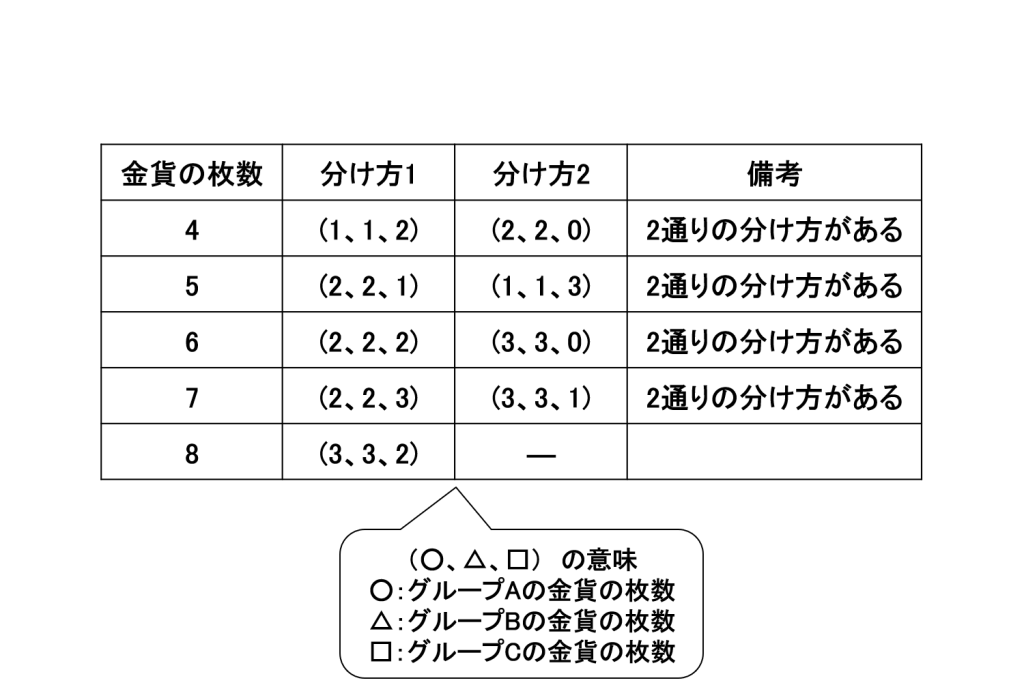
分け方1、分け方2とあるのは分け方が2種類あるということです。どちらの分け方でも構いません。

この分け方の下で、偽金貨を特定する手順は次のとおりです。
最初に、AとBを天秤にかけます。その結果は以下のいずれかになります。

A < B: 偽金貨はAグループに含まれます。
A > B: 偽金貨はBグループに含まれます。
A = B: 偽金貨はCグループに含まれます。

この結果に基づき、次の計測対象が決まります。
2回目の計測対象となるグループの金貨は1枚以上３枚以下に絞られますが、追加の計測は、グループの金貨が2枚または３枚の場合は1回、1枚の場合は不要（残った1枚が偽金貨で確定）となります。

したがって、合計1回または2回の計測で偽金貨を特定することが可能です。
これにより、金貨の枚数が4枚から8枚の場合でも、最悪2回の計測で偽金貨を見つけられることがわかりました。

8枚の場合の手順を下図に示します。

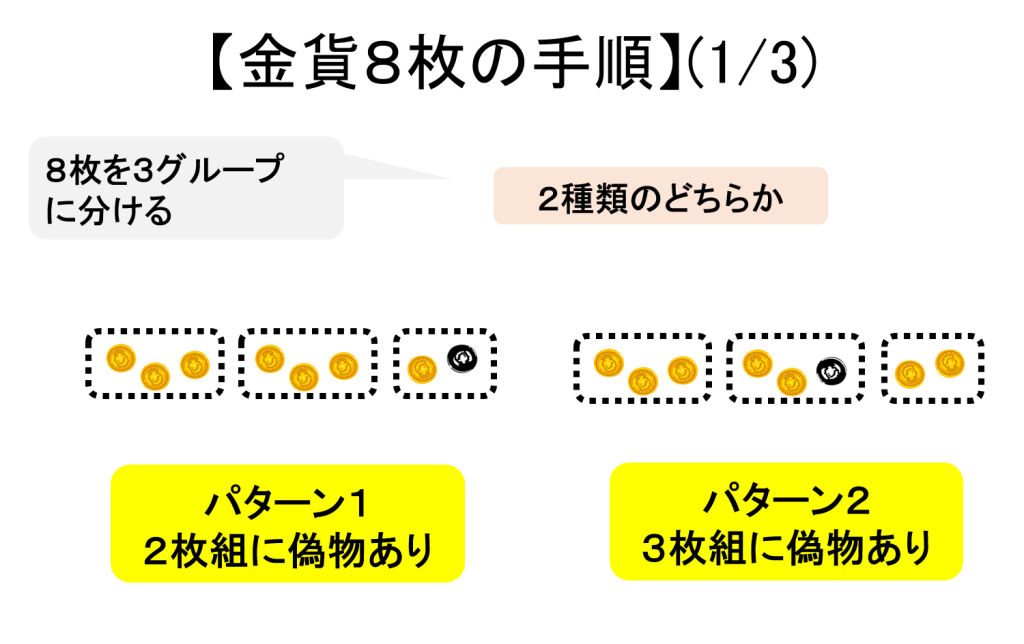
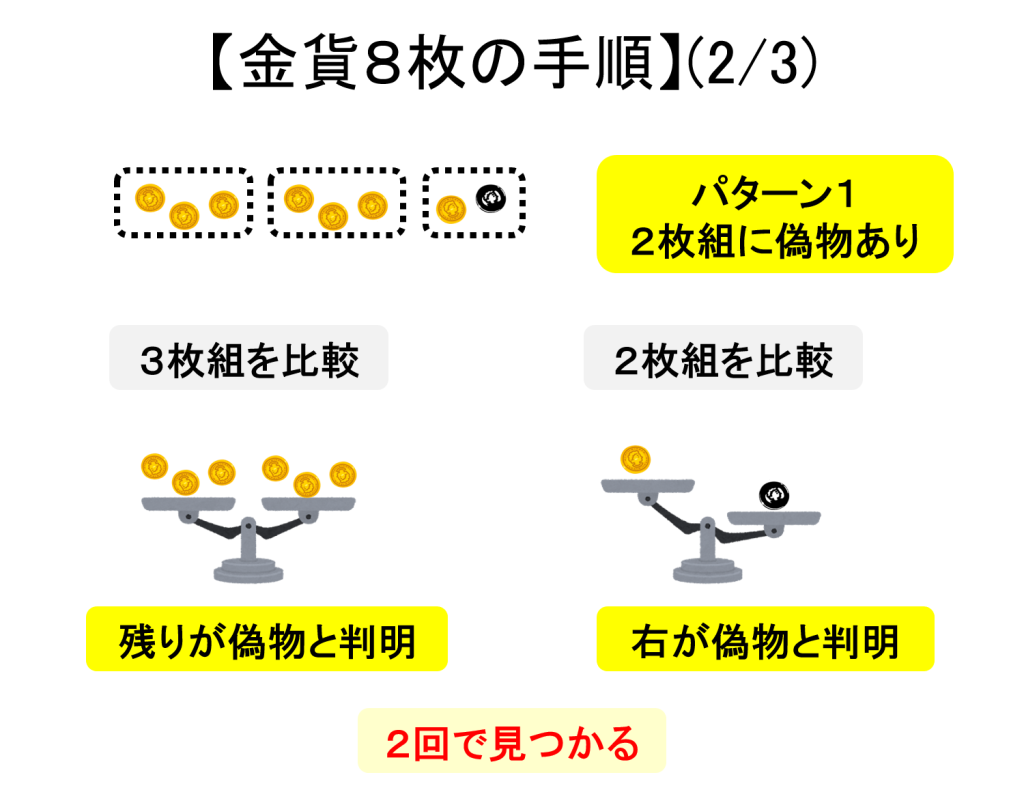
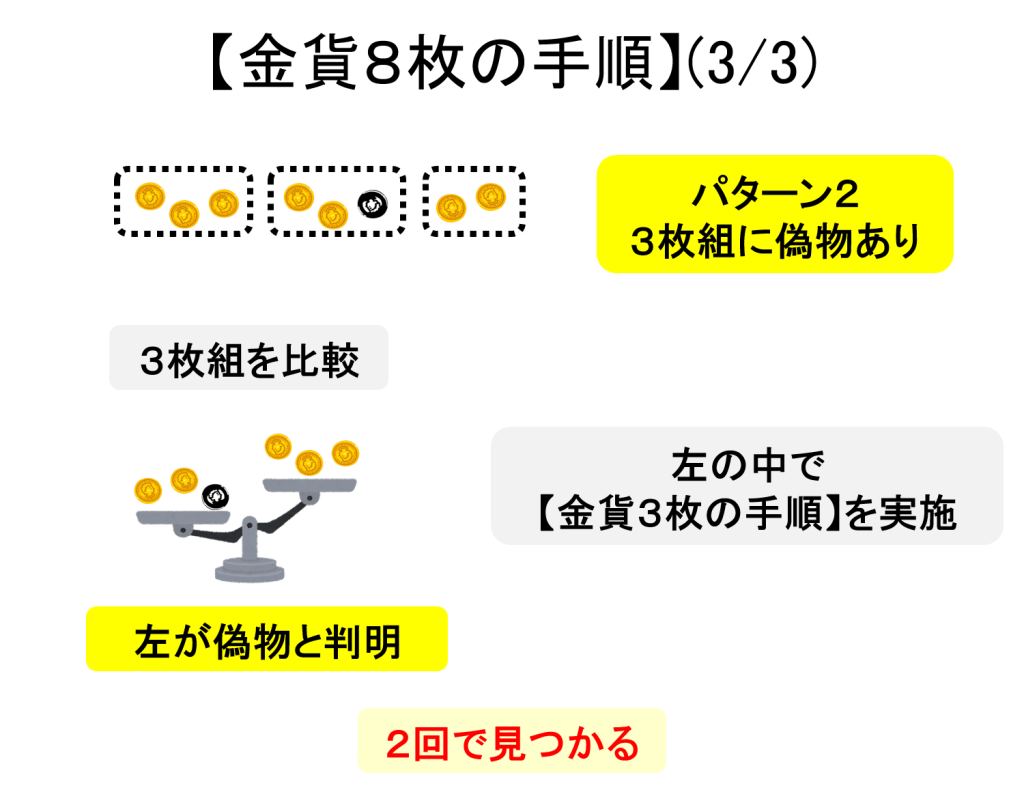
一般の場合は

この問題を一般化してみましょう。数式に不慣れな方は、下の表だけご覧ください。

金貨が N 枚（ 3 ^(k−1)+1≤N≤3^k ）ある場合、以下の2つの条件を満たすように3つのグループ（A、B、C）に分けることが鍵となります。

条件1: AグループとBグループの枚数を同数にする。
条件2: いずれのグループも 3 ^(k−1) 枚以下とする。

この分割は、N を3で割った余りに注目することで、次のように場合分けして実現できます。

場合1: N = 3nの場合（3で割り切れる場合）: A = B = n, C = n
場合2: N = 3n + 1の場合（3で割ると1余る場合）: A = B = n, C = n+1
場合3: N = 3n + 2の場合（3で割ると2余る場合）: A = B = n+1, C = n

このように分けることで、どのケースでも条件1と条件2を満たすことが確認できます。

（例えば、N = 3n + 1の場合、は以下の様にして示すことが出来ます。

3n + 1 ≤ 3 ^k → n + 1 ≤ 3 ^(k−1) + 2/3

           (n + 1), 3 ^(k−1) ともに整数なので、n + 1 ≤ 3 ^(k−1)

偽金貨を特定する手順は次のとおりです。まず、AグループとBグループを天秤に乗せます。結果は以下のいずれかになります。

• A＜B: Aグループが2回目の計測対象
• A＞B: Bグループが2回目の計測対象
• A＝B: Cグループが2回目の計測対象

この手順では、どの場合でも2回目の計測対象となるグループの枚数は 、グループ分けの方法から、3 ^(k−1) 枚以下です。

この分割と計測を繰り返すことで、（厳密には数学的帰納法を用いて）次の結論が導けます。

3 ^(k−1) <N≤3 ^k の場合、天秤を最大で k 回使うことで偽金貨を特定できます。

下にあるのは前回の回数をまとめた表の改訂版です。

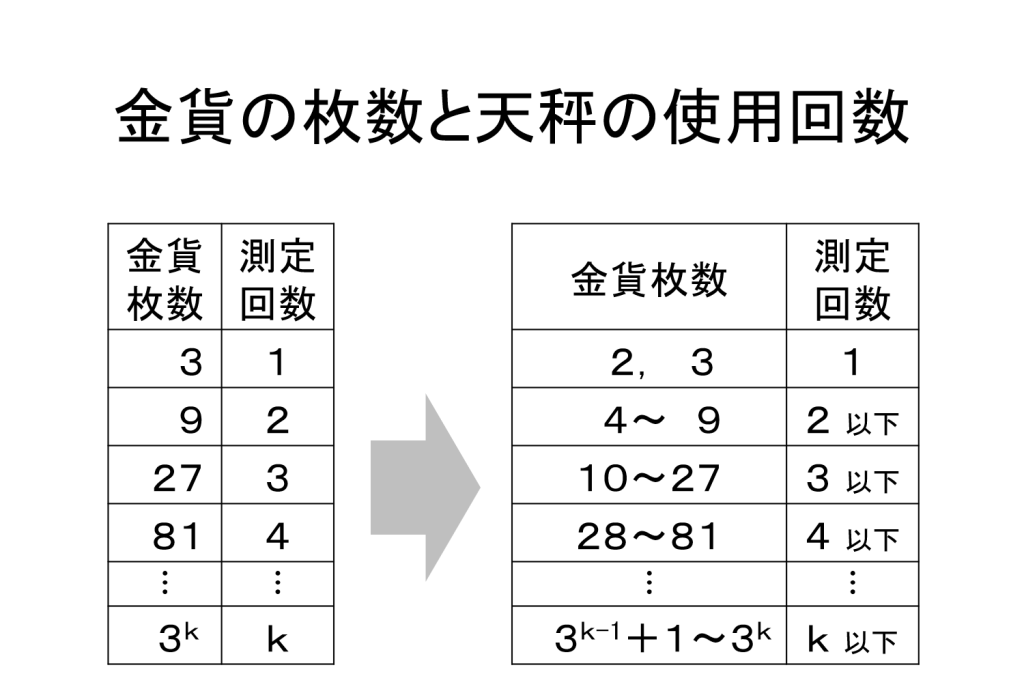
あとがき

この「偽金貨問題」には、

①偽物の軽重が不明、②偽物があるかどうか不明、③偽物が複数枚存在

など様々なバリエーションがあります。それに応じて様々な工夫が必要となり、解法の幅が広がります。ぜひ問題や解法を、いろいろと調べてみてください。

さて、偽金貨問題では、天秤で1回測るごとに、偽金貨の候補をどんどん絞り込んでいき、最終的には1枚の金貨に確定させることができました。
でも、紹介した方法が回数最小であることを厳密には示していません。ある出来事から得られる情報を「情報量」として数値化し、それを研究する「情報理論」という分野があります。

情報理論を用いると、必要な測定回数の下限やその他の問題の特性が求められます。非常に奥深い分野ですので、将来ぜひ興味を持って学んでみてください。

著者プロフィール 数学博識王みうら（三浦章）

■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。

ぜひ、お手にとってご覧ください！

数学博識王みうらの人気記事　こちらもどうぞ！