チェスを使った数学パズルをご存知ですか?
「ナイトツアー問題」や「エイトクイーン問題」など、面白い算数パズルが色々あります。
この記事では、前編に続き「ナイトの交換」について話しします。
■前回の記事はこちら!
2つの問題をもう一度見ましょう
「次回のお楽しみ」としたナイト交換(問題2)の解説です。(問題1)、(問題2)は次のようなものでした。
(問題1)
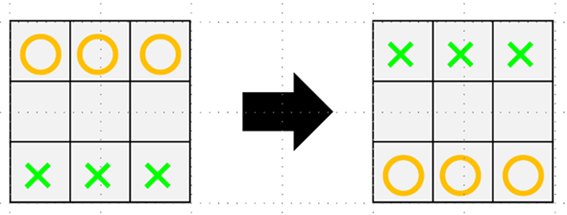
3×3マスのチェス盤に、○と×のナイトが3個ずつあります。 ○のナイトの所に×のナイト、×のナイトの所に○のナイトが来るようにナイトを移動させてください。つまり○と×の位置を交換してください。○と×のナイトはどんな順番で動かしても構いません。
(問題2)
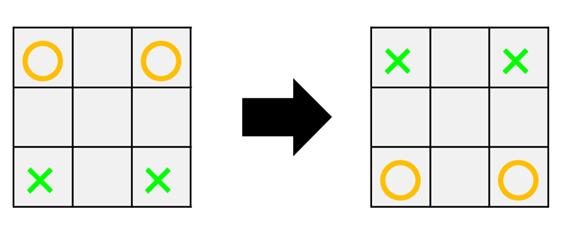
下図左のように○と×のナイトが2個ずつあります。 下図右のようにナイトを移動させてください。
(問題2)も、(問題1)と同じやり方で八角形上にナイトを置いて解くことが出来ます。
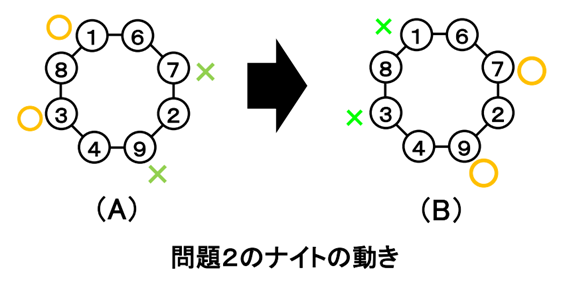
八角形上にナイトを置くと図のようになります。
そして矢印方向にすべてのナイトを動かすと移動完了です。チャレンジしてみてください。
(問題1)とは勝手が違って動かす回数の多いことが実感できます。疲れますよ。16手かかります。
問題2の方がむずかしい理由は?
ふつう、このようなパズルはコマ数を減らすと回数が減るのに、この場合は増えています。その原因を探ってみましょう。
まず(問題1)で6つのナイトそれぞれがどこに動いたかを分かるようにしてみましょう。
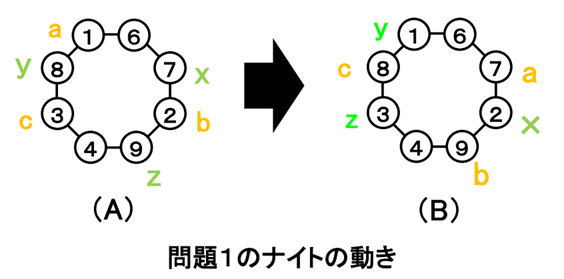
つまり、1、2、3の場所に置いたナイトには、a、b、cと印をつけ、7、8、9の場所に置いたナイトには x、y、zと印をつけます。
すると八角形上とマス目の上での配置は下のようになります。ナイトの移動した先がよくわかりますね。
チェス盤での配置の変化も見てみましょう。
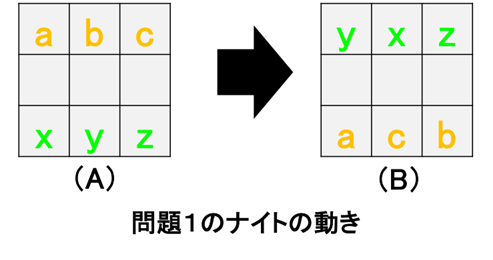
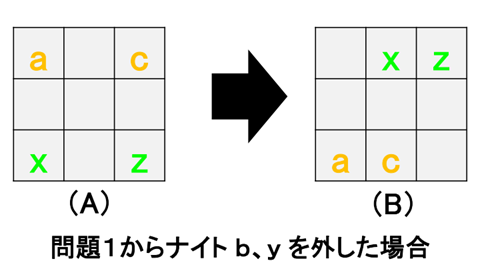
この出来上がりの状態でナイトの b、y を取り除くと、下の図のようになります。
つまり(問題1)の移動では、(問題2)の答えになっていないのです。
(問題1)の場合は、ナイト a、b、c は7、8、9の3箇所のいずれかに移動すれば良かったのに対して、(問題2)は、ナイト a、c の移動できる場所が 7、9 の2箇所のみとなる(8への移動は答えにならない)ため、動かし方の条件が(問題1)よりも厳しくなると言えます。
問題2を解くには
この状態から、(問題2)の最終形に向けてさらに移動させることも可能ですが、+10回必要です。
ということで、(問題2)を解くのでしたら、最初から考え直すのがお勧めです。
どのナイトがどこに動くのか、下の図に示します。参考にして下さい
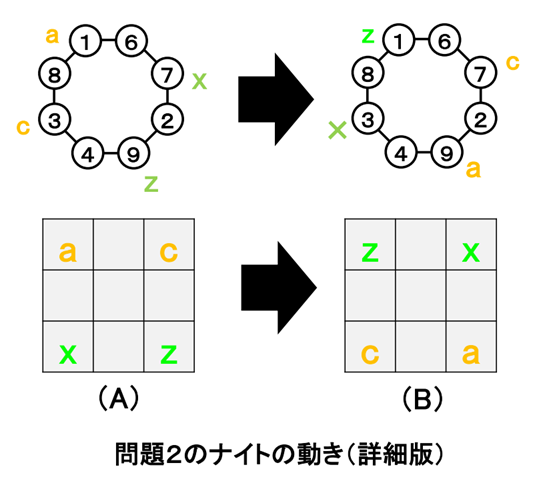
まとめると次のようになります。
(問題2)では、すべてのナイトを八角形上で、ちゃんと4回ずつ動かす必要があります。
それに対して、(問題1)では、すべてのナイトを4回動かす必要がありません。
これが(問題2)の方が、手順が複雑となる理由です。
なお、(問題2)では、実際に移動させなくても、次のようにして、手数は計算できます。
ナイト1個につき反対側への移動回数は4回。八角形の周上で追い越しがないので、移動の手数=4回×ナイトの数。従って、ナイトが4個のとき 移動の手数=4回×4=16回。
おわりに……頂点と辺の関係に注目する「グラフ理論」
問題を解くためには、頂点とそれを結ぶ辺の関係だけに注目して道筋の図形を八角形に変形しました。
まさに発想の転換といえます。
このように頂点と辺の関係に関わる理論をグラフ理論といいます。
前に紹介した一筆書きもグラフ理論に関係しています。
グラフ理論は身の回りの事柄に関係する非常に実用的価値の高い理論です。ぜひ、勉強してみてはいかがでしょうか。
【参考文献】
aha! Insight ひらめき思考 1 、日経サイエンス社、2009/10/1 ガードナー,マーチン著、島田一男訳











