こんにちは、みうらです。
いきなりですが、次のような状況を考えてみましょう。
X町には、なんともユニークな3軒の食料品店、A商店、B商店、C商店が並んでいます。この町の人々はいつもこの3店舗の「お得合戦」に大注目。今日もまた、新しいキャンペーンが勃発しました!
A商店の勝負:買えばもらえる!
A商店は開店10周年記念セールを開催中。「缶ジュース4本買ったら、1本おまけでプレゼント!」という太っ腹なキャンペーンです。つまり、4本の支払いで5本ゲット。ジュース好きにはたまりません。
B商店の作戦:飲み終わればもらえる!
B商店も負けていられません。「空缶4本持ってきたら、1本無料で差し上げます!」という斬新な企画を打ち出しました。つまり、飲んだ後の缶まで大事にすれば、もう1本楽しめるというわけです。
C商店の本気:買っても飲んでももらえる!
ところがC商店、さすがの行動力。「負けてはならじ」と、A商店とB商店のいいとこ取りで、なんと「缶ジュース4本買ったら1本無料、さらに空缶4本持ってきたらもう1本無料!」という究極のお得サービスを開始!ジュース好きが泣いて喜ぶ、夢のようなキャンペーンです。
どちらが得?
さて、A商店の「事前おまけ」とB商店の「事後おまけ」、どちらのお店がお得でしょうか? そして、C商店が圧倒的得なことはわかりますが、果たしてどのくらい得なのでしょう。
この記事では、これらを華麗に解く方法を2回に分けてご紹介します。
今回は四則演算の範囲で説明し、次回は中学生や高校生の皆さんのも楽しんで(感心して?)いただけるように、文字式を交えて説明をしたいと思います。
具体的な問題に直してみよう
まずはA商店、B商店、C商店の企画を、問題らしい形に直して、具体的に考えてみましょう。
問題1) 缶ジュースを4本買うと、新品の缶ジュース1本をおまけにくれます。18本購入すると、おまけは何本ですか。
問題2) 飲んだ後の空缶を4個持って行くと、新品のジュース1本をおまけにくれます。18本購入すると、おまけは何本ですか。
問題3) 缶ジュースを4本買うと、新品のジュース1本をおまけにくれます。また、飲んだ後の空缶を4個持って行くと、新品のジュース1本をおまけにくれます。18本購入すると、おまけは何本ですか。
この “問題2) B商店の問題”は、「缶ジュースの問題」「空き缶問題」「空きビン問題」等と呼ばれ、中学受験界隈ではわりに有名なようです。
問題1の解法
これは簡単ですね。
おまけの本数=(買った本数)÷(交換に必要な本数)
です。従って、
18÷4=4…2
ですから、4本余分に飲めます。
問題2のよく知られている解法
解法としては、以下のような方法がよく紹介されています。
方法1)交換の状況を文章で表現し、数えあげる
方法2)おまけの本数の規則性を見つける
試しにこの問題を方法1,2で解いてみましょう。
方法1) 交換の状況を文章で表現し、数えあげる
① 最初にジュースは18本ある
② その結果、18個の空き缶ができる
③ 18個の空缶を交換する。18÷4=4…2
→4本のジュースが追加でもらえる。空缶が2個余る。
④ ③で追加にもらったジュースの空き缶を加えて、空き缶は4+2=6個 となる
⑤ 6÷4=1…1 → 1本のジュースが追加でもらえる。空き缶が1個余る
従って、飲めるジュースは全部で 18+4+1=23本 となる
多少なりとも分かりやすくするためには、次のような図が有効です。
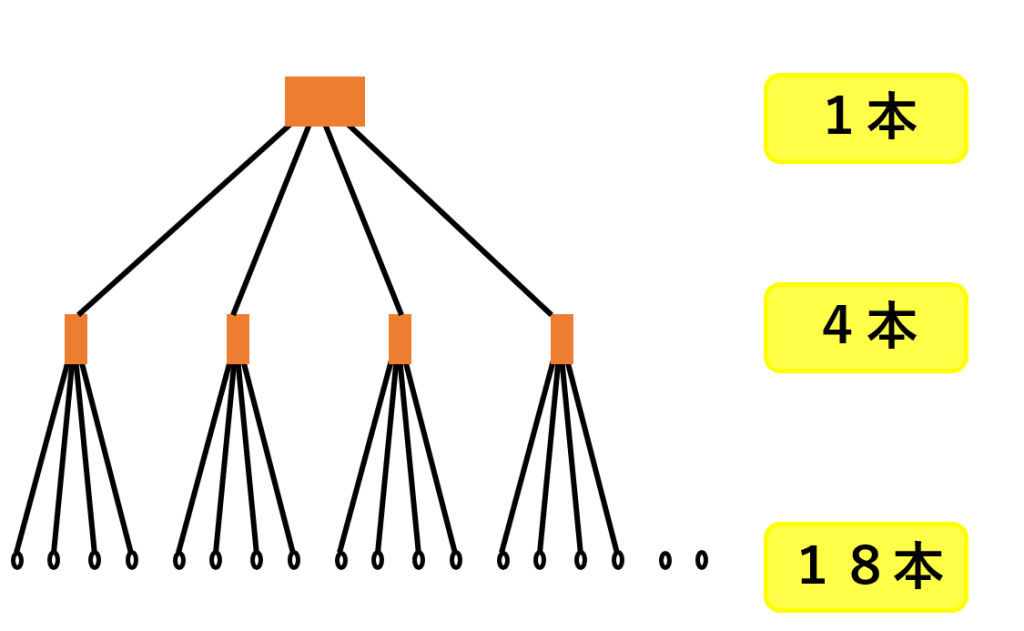
見てのとおり分かりやすいですが、18本も缶?の形を書くのは大変です。そこで少し改良した下の図を考えました。
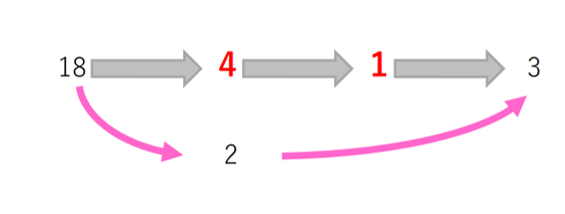
上段に書いたのは空缶の個数、そのうちゲットした個数は赤字です。下段はゲットする際に使わなかった個数です。最初の図より簡単ですが、やはり面倒ですね。
方法2) 規則性を考える
購入本数と飲める本数の対応を考え、次のような表を作ります。
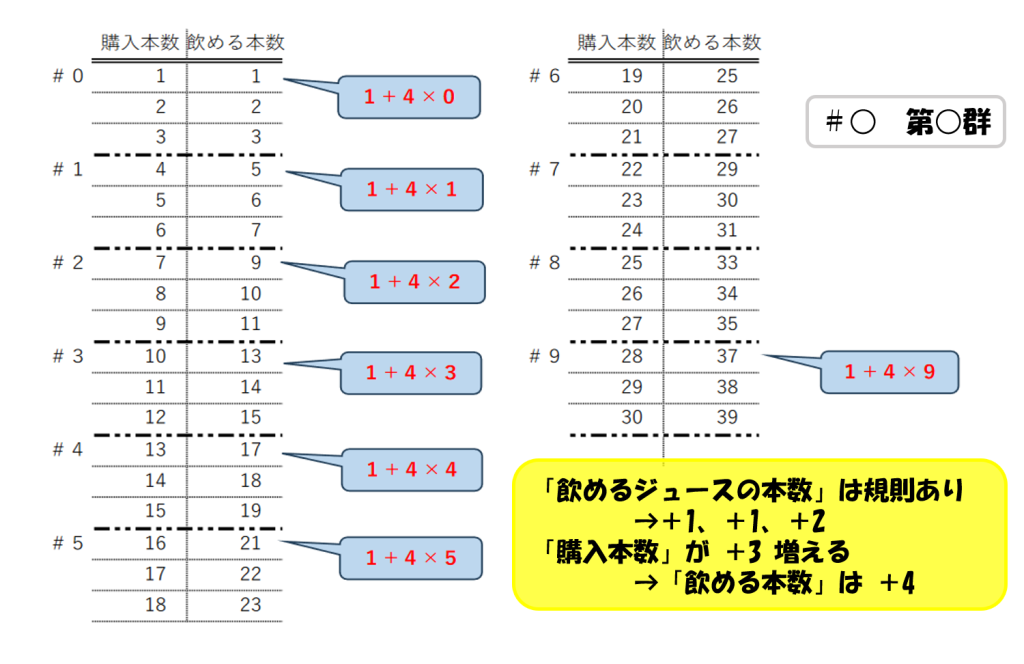
問題2の抜本的かつ画期的な解法
いかがでしょう。方法1,2を使い、丹念にそして正確に計算すると本数を求めることはできます。
しかし、「1000本、10000本買うと何本おまけがもらえますか」などのように本数が多くなると手間がかかります。
そこで、問題2を解決する抜本的かつ画期的な解法をご紹介し、それを用いて、1000本、10000本にも挑んでみましょう。
解法) まず缶ジュースの置き場所を下のように3カ所設けます。
場所1:缶ジュースを1本置きます。
場所2:缶ジュース (18-1)本を(4-1)本をひとまとめにしたものを束にして置きます。束には、左からB1,B2,…,B5 と名前を付けます。束は、(18-1)÷(4-1)=5…2 ですから、5つできます。
場所3:残りの缶ジュースを置きます。18-1-3×5=2 本 置くことになります。
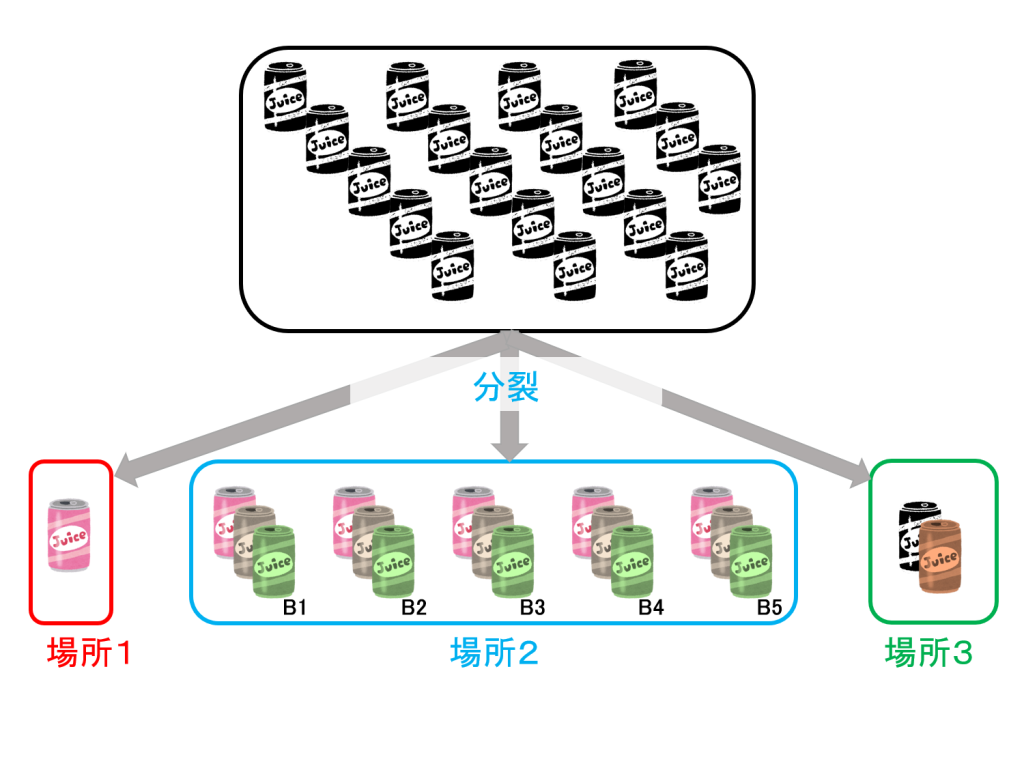
これから、実際に飲んで交換を始めます。場所1にある缶ジュースと場所2にある缶ジュース1束を組み合わせると 缶ジュース 4 本の集まりができます。それらを飲み切ると、1本おまけがもらえます。このおまけを場所1に置きます。この模様を下図に示します。場所2にある束から選ぶ1束は任意でよいのですが、この図では場所1と場所2中のB1を組み合わせたものを示しています。
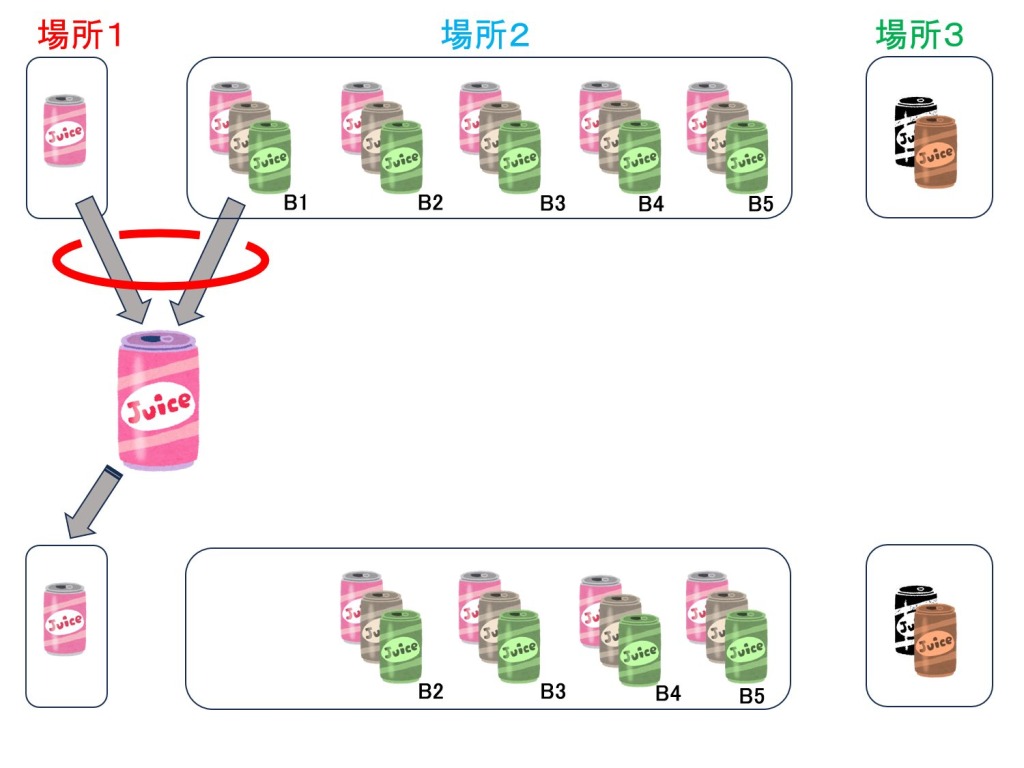
以下同様に、場所1の1缶と場所2の1束を組み合わせて、おまけの交換を繰り返します。束の数(5束)回繰り返した後は、場所1に1本と場所3に2本残ります。残った缶は、合わせても、3本 、つまり4本に足りません。従って、空缶にしたところで、おまけがもらえる個数にならないので、これで終わりです。結局おまけは、交換した回数(=束の数)と同じで
5 本
もらったことになります。
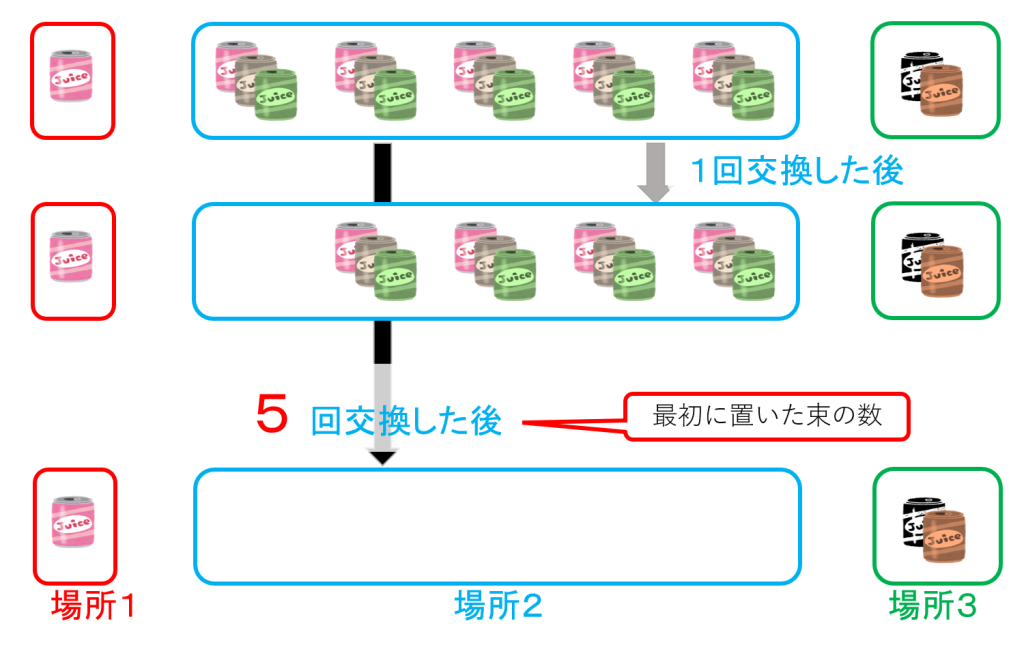
いかがでしょう。お分かりになりましたか。缶ジュースを規則に従って、場所1,2,3におくということを思い浮かべれば、
おまけの本数=「(買った本数-1)÷(交換に必要な本数―1)」の商の整数部分
で一発で出せます。この調子で、1000本でも,10000本でも片付けることが出来ます。
1000本の場合は、
おまけの本数=「(買った本数-1)÷(交換に必要な本数―1)」の商の整数部分
=(1000-1)÷(4―1)=999÷3=333本
10000本の場合は、
おまけの本数=「(買った本数-1)÷(交換に必要な本数―1)」の商の整数部分
=(10000-1)÷(4―1)=9999÷3=3333本
となります。
問題3の解法
問題1から缶ジュースは18+4=22本飲めることが分かります。この22本の空缶を缶ジュースに交換すると
(22-1)÷(4-1)=7本
ゲットできます。合わせて、
22+7=29本
飲めることが分かります。18本分のお金で29本も飲めます。C商店の圧倒的なお得感が際立ちますね!
おわりに
どうでしょうか?空缶がおまけの缶を生むという、一見とらえどころのない問題も、空缶を3つの場所に分割して配置する画期的な方法を使えば、簡単に解けることがお分かりいただけたのではないでしょうか。次回は、この方法を文字式を交えて一般化してみます。どうぞお楽しみに!
著者プロフィール 数学博識王みうら(三浦章)

みうら(三浦 章) math channelマガジン数学博識王
国立市在住。東京工業大学大学院修士課程を修了後、通信キャリヤで30年ほど通信サービスの研究実用化に従事。15年ほど前に、大学教員に転身。情報システム、数学、問題解決フレームワーク等を教えてきました。5年ほど前から地元公民館で月2回程度市民向け数学教室も開催しています。近頃は数学的背景のあるパズルに興味があり、その内容の発信にも関心があります。博士号(工学)、高校教員免許(数学)あり。
■数学博識王みうらが執筆に携わったmath channelマガジンの本

ビジネスや生活から、エンタメや入試問題まで、中学生から読める、身近で、おもしろくて、役に立つ、数学の話をまとめた一冊です。
「算数・数学は面白いもの・楽しいもの」と思ってもらいたいという思いから、math channelマガジン編集部メンバーがアイデアを出し合いながら書きました。
ぜひ、お手にとってご覧ください!